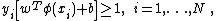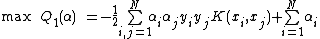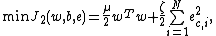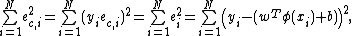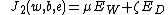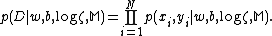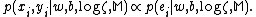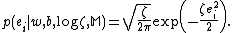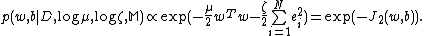Least squares support vector machine
Encyclopedia
Least squares support vector machines (LS-SVM) are least squares
versions of support vector machine
s (SVM), which are a set of related supervised learning
methods that analyze data and recognize patterns, and which are used for classification and regression analysis
. In this version one finds the solution by solving a set of linear equation
s instead of a convex quadratic programming
(QP) problem for classical SVMs. Least squares SVM classifiers, were proposed by Suykens and Vandewalle. LS-SVMs are a class of kernel based learning methods.
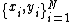 with input data
with input data  and corresponding binary class labels
and corresponding binary class labels 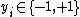 , the SVM
, the SVM
classifier, according to Vapnik’s original formulation, satisfies the following conditions:
Least squares
The method of least squares is a standard approach to the approximate solution of overdetermined systems, i.e., sets of equations in which there are more equations than unknowns. "Least squares" means that the overall solution minimizes the sum of the squares of the errors made in solving every...
versions of support vector machine
Support vector machine
A support vector machine is a concept in statistics and computer science for a set of related supervised learning methods that analyze data and recognize patterns, used for classification and regression analysis...
s (SVM), which are a set of related supervised learning
Supervised learning
Supervised learning is the machine learning task of inferring a function from supervised training data. The training data consist of a set of training examples. In supervised learning, each example is a pair consisting of an input object and a desired output value...
methods that analyze data and recognize patterns, and which are used for classification and regression analysis
Regression analysis
In statistics, regression analysis includes many techniques for modeling and analyzing several variables, when the focus is on the relationship between a dependent variable and one or more independent variables...
. In this version one finds the solution by solving a set of linear equation
Linear equation
A linear equation is an algebraic equation in which each term is either a constant or the product of a constant and a single variable....
s instead of a convex quadratic programming
Quadratic programming
Quadratic programming is a special type of mathematical optimization problem. It is the problem of optimizing a quadratic function of several variables subject to linear constraints on these variables....
(QP) problem for classical SVMs. Least squares SVM classifiers, were proposed by Suykens and Vandewalle. LS-SVMs are a class of kernel based learning methods.
From support vector machine to least squares support vector machine
Given a training set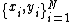 with input data
with input data  and corresponding binary class labels
and corresponding binary class labels 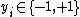 , the SVM
, the SVMSVM
SVM can refer to:* SVM * Saskatchewan Volunteer Medal* Scanning voltage microscopy* Schuylkill Valley Metro* Secure Virtual Machine, or AMD Virtualization , a virtualization technology by AMD* Solaris Volume Manager...
classifier, according to Vapnik’s original formulation, satisfies the following conditions:
-
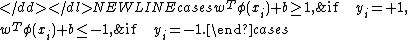
Which is equivalent to
where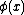 is the nonlinear map from original space to the high (and possibly infinite) dimensional space.
is the nonlinear map from original space to the high (and possibly infinite) dimensional space.
Inseparable data
In case of such separating hyperplane does not exist, we introduce a so called slack variable such that
such that
-
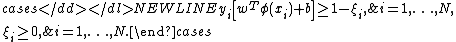
According to the structural risk minimizationStructural risk minimizationStructural risk minimization is an inductive principle of use in machine learning. Commonly in machine learning, a generalized model must be selected from a finite data set, with the consequent problem of overfitting – the model becoming too strongly tailored to the particularities of the...
principle, the risk bound is minimized by the following minimization problem:
-
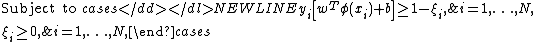
where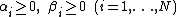 are the Lagrangian multipliers. The optimal point will in the saddle pointSaddle pointIn mathematics, a saddle point is a point in the domain of a function that is a stationary point but not a local extremum. The name derives from the fact that in two dimensions the surface resembles a saddle that curves up in one direction, and curves down in a different direction...
are the Lagrangian multipliers. The optimal point will in the saddle pointSaddle pointIn mathematics, a saddle point is a point in the domain of a function that is a stationary point but not a local extremum. The name derives from the fact that in two dimensions the surface resembles a saddle that curves up in one direction, and curves down in a different direction...
of the Lagrangian function, and then we obtain
-
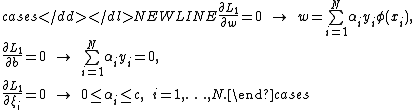
By substituting w by its expression, we will get the following quadratic programming problem:
where is called the kernel function. Solving this QP problem subject to constrains in (8), we will get the hyperplaneHyperplaneA hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
is called the kernel function. Solving this QP problem subject to constrains in (8), we will get the hyperplaneHyperplaneA hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
in the high dimensional space and hence the classifierClassifierClassifier may refer to:*Classifier *Classifier *Classifier *Hierarchical classifier*Linear classifier...
in the original space.
Least squares SVM formulation
The least squares version of the SVM classifier is obtained by reformulating the minimization problem as:
subject to the equality constraints:
The least squares SVM (LS-SVM) classifier formulation above implicitly corresponds to a regressionRegression analysisIn statistics, regression analysis includes many techniques for modeling and analyzing several variables, when the focus is on the relationship between a dependent variable and one or more independent variables...
interpretation with binary targets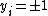 .
.
Using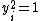 , we have
, we have
with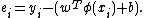
Hence the LS-SVM classifier formulation is equivalent to
with and
and 
Both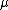 and
and  should be considered as hyperparamters to tune the amount of regularization versus the sum squared error. The solution does only depend on the ratio
should be considered as hyperparamters to tune the amount of regularization versus the sum squared error. The solution does only depend on the ratio  , therefore the original formulation uses only
, therefore the original formulation uses only 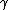 as tuning parameter. We use both
as tuning parameter. We use both 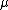 and
and 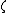 as parameters in order to provide a Bayesian interpretation to LS-SVM.
as parameters in order to provide a Bayesian interpretation to LS-SVM.
The solution of LS-SVM regressor will be obtained after we construct the Lagrangian function:
-
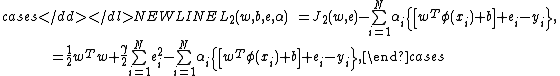
where are the Lagrange multipliers. The conditions for optimality are
are the Lagrange multipliers. The conditions for optimality are
-
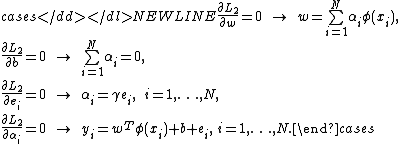
Elimination of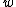 and
and  will yield a linear systemLinear systemA linear system is a mathematical model of a system based on the use of a linear operator.Linear systems typically exhibit features and properties that are much simpler than the general, nonlinear case....
will yield a linear systemLinear systemA linear system is a mathematical model of a system based on the use of a linear operator.Linear systems typically exhibit features and properties that are much simpler than the general, nonlinear case....
instead of a quadratic programmingQuadratic programmingQuadratic programming is a special type of mathematical optimization problem. It is the problem of optimizing a quadratic function of several variables subject to linear constraints on these variables....
problem:
-
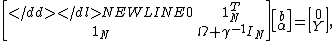
with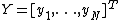 ,
, 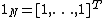 and
and 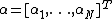 . Here,
. Here,  is an
is an  identity matrixIdentity matrixIn linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
identity matrixIdentity matrixIn linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
, and is the kernel matrix defined by
is the kernel matrix defined by 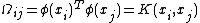 .
.
Kernel function K
For the kernel function K(•, •) one typically has the following choices:- LinearLinearIn mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
kernel :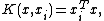
- PolynomialPolynomialIn mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
kernel of degree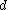 :
: 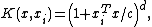
- Radial basis functionRadial basis functionA radial basis function is a real-valued function whose value depends only on the distance from the origin, so that \phi = \phi; or alternatively on the distance from some other point c, called a center, so that \phi = \phi...
RBF kernel :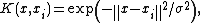
- MLP kernel :
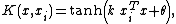
where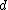 ,
,  ,
,  ,
, 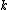 and
and 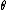 are constants. Notice that the Mercer condition holds for all
are constants. Notice that the Mercer condition holds for all 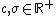 and
and 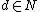 values in the polynomialPolynomialIn mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
values in the polynomialPolynomialIn mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
and RBF case, but not for all possible choices of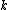 and
and 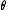 in the MLP case. The scale parameters
in the MLP case. The scale parameters  ,
,  and
and  determine the scaling of the inputs in the polynomial, RBF and MLP kernel function. This scaling is related to the bandwidth of the kernel in statisticsStatisticsStatistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
determine the scaling of the inputs in the polynomial, RBF and MLP kernel function. This scaling is related to the bandwidth of the kernel in statisticsStatisticsStatistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, where it is shown that the bandwidth is an important parameter of the generalization behavior of a kernel method.
Bayesian interpretation for LS-SVM
A BayesianBayesianBayesian refers to methods in probability and statistics named after the Reverend Thomas Bayes , in particular methods related to statistical inference:...
interpretation of the SVM has been proposed by Smola et al. They showed that the use of different kernels in SVM can be regarded as defining different prior probabilityPrior probabilityIn Bayesian statistical inference, a prior probability distribution, often called simply the prior, of an uncertain quantity p is the probability distribution that would express one's uncertainty about p before the "data"...
distributions on the functional space, as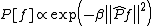 . Here
. Here 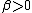 is a constant and
is a constant and  is the regularization operator corresponding to the selected kernel.
is the regularization operator corresponding to the selected kernel.
A general Bayesian evidence framework was developed by MacKay, and MacKay has used it to the problem of regression, forward neural networkNeural networkThe term neural network was traditionally used to refer to a network or circuit of biological neurons. The modern usage of the term often refers to artificial neural networks, which are composed of artificial neurons or nodes...
and classification network. Provided data set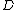 , a model
, a model 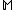 with parameter vector
with parameter vector  and a so called hyperparameter or regularization parameter
and a so called hyperparameter or regularization parameter 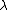 , Bayesian inferenceBayesian inferenceIn statistics, Bayesian inference is a method of statistical inference. It is often used in science and engineering to determine model parameters, make predictions about unknown variables, and to perform model selection...
, Bayesian inferenceBayesian inferenceIn statistics, Bayesian inference is a method of statistical inference. It is often used in science and engineering to determine model parameters, make predictions about unknown variables, and to perform model selection...
is constructed with 3 levels of inference:
- In level 1, for a given value of
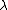 , the first level of inference infers the posterior distribution of by Bayesian rule
, the first level of inference infers the posterior distribution of by Bayesian rule
-

- The second level of inference determines the value of
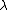 , by maximizing
, by maximizing
-
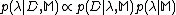
- The third level of inference in the evidence framework ranks different models by examining their posterior probabilities
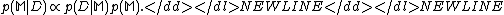
We can see that Bayesian evidence framework is a unified theory for learningLearningLearning is acquiring new or modifying existing knowledge, behaviors, skills, values, or preferences and may involve synthesizing different types of information. The ability to learn is possessed by humans, animals and some machines. Progress over time tends to follow learning curves.Human learning...
the model and model selection.
Kwok used the Bayesian evidence framework to interpret the formulation of SVM and model selection. And he also applied Bayesian evidence framework to support vector regression.
Now, given the data points and the hyperparameters
and the hyperparameters 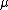 and
and 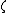 of the model
of the model  , the model parameters
, the model parameters 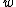 and
and 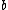 are estimated by maximizing the posterior
are estimated by maximizing the posterior  . Applying Bayes’ rule, we obtain:
. Applying Bayes’ rule, we obtain:
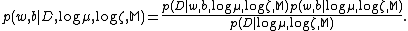
Where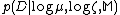 is a normalizing constant such the integral over all possible
is a normalizing constant such the integral over all possible 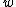 and
and 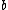 is equal to 1.
is equal to 1.
We assume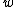 and
and 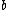 are independent of the hyperparameter
are independent of the hyperparameter  , and are conditional independent, i.e., we assume
, and are conditional independent, i.e., we assume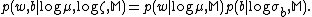
When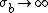 , the distribution of
, the distribution of 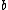 will approximate a uniform distribution. Furthermore, we assume
will approximate a uniform distribution. Furthermore, we assume 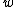 and
and  are Gaussian distribution, so we obtain the a priori distribution of
are Gaussian distribution, so we obtain the a priori distribution of 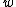 and
and 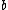 with
with 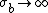 to be:
to be:
-
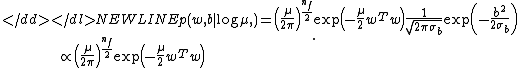
Here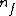 is the dimensionality of the feature space, same as the dimensionality of
is the dimensionality of the feature space, same as the dimensionality of 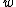 .
.
The probability of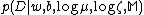 is assumed to depend only on
is assumed to depend only on 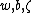 and
and 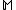 . We assume that the data points are independently identically distributed (i.i.d.), so that:
. We assume that the data points are independently identically distributed (i.i.d.), so that:
In order to obtain the least square cost function, it is assumed that the probability of a data point is proportional to:
A Gaussian distribution is taken for the errors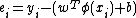 as:
as:
It is assumed that the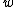 and
and 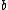 are determined in such a way that the class centers
are determined in such a way that the class centers 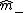 and
and 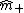 are mapped onto the target -1 and +1, respectively. The projections
are mapped onto the target -1 and +1, respectively. The projections 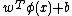 of the class elements
of the class elements 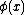 follow a multivariate Gaussian distribution, which have variance
follow a multivariate Gaussian distribution, which have variance 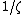 .
.
Combining the preceding expressions, and neglecting all constants, Bayes’ rule becomes
The maximum posterior density estimates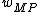 and
and  are then be obtained by minimizing the negative logarithm of (26), so we arrive (10).
are then be obtained by minimizing the negative logarithm of (26), so we arrive (10).
External links
- www.esat.kuleuven.be/sista/lssvmlab/ "Least squares support vector machine Lab (LS-SVMlab) toolbox contains Matlab/C implementations for a number of LS-SVM algorithms."
- www.kernel-machines.org "Support Vector Machines and Kernel based methods (Smola & Schölkopf)."
- www.gaussianprocess.org "Gaussian Processes: Data modeling using Gaussian Process priors over functions for regression and classification (MacKay, Williams)"
- www.support-vector.net "Support Vector Machines and kernel based methods (Cristianini)"
- dlib: Contains a least-squares SVM implementation for large-scale datasets.
-
-
- The second level of inference determines the value of
- Linear
-
-
-
-
-
-