Diagram (category theory)
Encyclopedia
In category theory
, a branch of mathematics, a diagram is the categorical analogue of an indexed family
in set theory
. The primary difference is that in the categorical setting one has morphism
s. An indexed family of sets is a collection of sets, indexed by a fixed set; equivalently, a function from a fixed index set to the class of sets. A diagram is a collection of objects and morphisms, indexed by a fixed category; equivalently, a functor from a fixed index category to some category.
Diagrams are used in the definition of limit and colimits
and the related notion of cone
s.
C is a (covariant) functor
The category J is called the index category or the scheme of the diagram D. The actual objects and morphisms in J are largely irrelevant, only the way in which they are interrelated matters. The diagram D is thought of as indexing a collection of objects and morphisms in C patterned on J.
Although, technically, there is no difference between an individual diagram and a functor or between a scheme and a category, the change in terminology reflects a change in perspective, just as in the set theoretic case: one fixes the index category, and allows the functor (and, secondarily, the target category) to vary.
One is most often interested in the case where the scheme J is a small or even finite category. A diagram is said to be small or finite whenever J is.
A morphism of diagrams of type J in a category C is a natural transformation
between functors. One can then interpret the category of diagrams of type J in C as the functor category
CJ, and a diagram is then an object in this category.
of a diagram D : J → C is a morphism from the constant diagram Δ(N) to D. The constant diagram is the diagram which sends every object of J to an object N of C and every morphism to the identity morphism on N.
The limit
of a diagram D is a universal cone to D. That is, a cone through which all other cones uniquely factor. If the limit exists in a category C for all diagrams of type J one obtains a functor
which sends each diagram to its limit.
Dually, the colimit of diagram D is a universal cone from D. If the colimit exists for all diagrams of type J one has a functor
which sends each diagram to its colimit.
Not every diagram commutes, as not every index category is a poset category:
most simply, the diagram of a single object with an endomorphism (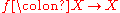
), or with two parallel arrows (
; 
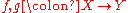) need not commute. Further, diagrams may be impossible (because infinite) or messy (because many objects or morphisms) to draw; however, schematic commutative diagrams (for subcategories of the index category, or with ellipses, such as for a directed system) are used to clarify such complex diagrams.
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, a branch of mathematics, a diagram is the categorical analogue of an indexed family
Indexed family
In mathematics, an indexed family is a collection of values that are associated with indexes. For example, a family of real numbers, indexed by the integers is a collection of real numbers, where each integer is associated with one of the real numbers....
in set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
. The primary difference is that in the categorical setting one has morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
s. An indexed family of sets is a collection of sets, indexed by a fixed set; equivalently, a function from a fixed index set to the class of sets. A diagram is a collection of objects and morphisms, indexed by a fixed category; equivalently, a functor from a fixed index category to some category.
Diagrams are used in the definition of limit and colimits
Limit (category theory)
In category theory, a branch of mathematics, the abstract notion of a limit captures the essential properties of universal constructions such as products and inverse limits....
and the related notion of cone
Cone (category theory)
In category theory, a branch of mathematics, the cone of a functor is an abstract notion used to define the limit of that functor. Cones make other appearances in category theory as well.-Definition:...
s.
Definition
Formally, a diagram of type J in a categoryCategory (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
C is a (covariant) functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
- D : J → C
The category J is called the index category or the scheme of the diagram D. The actual objects and morphisms in J are largely irrelevant, only the way in which they are interrelated matters. The diagram D is thought of as indexing a collection of objects and morphisms in C patterned on J.
Although, technically, there is no difference between an individual diagram and a functor or between a scheme and a category, the change in terminology reflects a change in perspective, just as in the set theoretic case: one fixes the index category, and allows the functor (and, secondarily, the target category) to vary.
One is most often interested in the case where the scheme J is a small or even finite category. A diagram is said to be small or finite whenever J is.
A morphism of diagrams of type J in a category C is a natural transformation
Natural transformation
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
between functors. One can then interpret the category of diagrams of type J in C as the functor category
Functor category
In category theory, a branch of mathematics, the functors between two given categories form a category, where the objects are the functors and the morphisms are natural transformations between the functors...
CJ, and a diagram is then an object in this category.
Examples
- If J is a (small) discrete categoryDiscrete categoryIn mathematics, especially category theory, a discrete category is a category whose only morphisms are the identity morphisms. It is the simplest kind of category...
, then a diagram of type J is essentially just an indexed family of objects in C (indexed by J).
- If J is a poset category then a diagram of type J is a family of objects Di together with a unique morphism fij : Di → Dj whenever i ≤ j. If J is directedDirected setIn mathematics, a directed set is a nonempty set A together with a reflexive and transitive binary relation ≤ , with the additional property that every pair of elements has an upper bound: In other words, for any a and b in A there must exist a c in A with a ≤ c and b ≤...
then a diagram of type J is called a direct system of objects and morphisms. If the diagram is contravariant then it is called an inverse systemInverse systemIn mathematics, an inverse system in a category C is a functor from a small cofiltered category I to C. An inverse system is sometimes called a pro-object in C. The dual concept is a direct system.-The category of inverse systems:...
.
- If
, then a diagram of type J (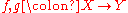
) is called "two parallel morphisms": its limit is an equalizer, and its colimit is a coequalizerCoequalizerIn category theory, a coequalizer is a generalization of a quotient by an equivalence relation to objects in an arbitrary category...
.
- If J = -1 ← 0 → +1, then a diagram of type J (A ← B → C) is a spanSpan (category theory)A span, in category theory, is a generalization of the notion of relation between two objects of a category. When the category has all pullbacks , spans can be considered as morphisms in a category of fractions....
, and its colimit is a pushoutPushout (category theory)In category theory, a branch of mathematics, a pushout is the colimit of a diagram consisting of two morphisms f : Z → X and g : Z → Y with a common domain: it is the colimit of the span X \leftarrow Z \rightarrow Y.The pushout is the...
.
- If J = -1 → 0 ← +1, then a diagram of type J (A → B ← C) is a cospan, and its limit is a pullbackPullback (category theory)In category theory, a branch of mathematics, a pullback is the limit of a diagram consisting of two morphisms f : X → Z and g : Y → Z with a common codomain; it is the limit of the cospan X \rightarrow Z \leftarrow Y...
.
Cones and limits
A coneCone (category theory)
In category theory, a branch of mathematics, the cone of a functor is an abstract notion used to define the limit of that functor. Cones make other appearances in category theory as well.-Definition:...
of a diagram D : J → C is a morphism from the constant diagram Δ(N) to D. The constant diagram is the diagram which sends every object of J to an object N of C and every morphism to the identity morphism on N.
The limit
Limit (category theory)
In category theory, a branch of mathematics, the abstract notion of a limit captures the essential properties of universal constructions such as products and inverse limits....
of a diagram D is a universal cone to D. That is, a cone through which all other cones uniquely factor. If the limit exists in a category C for all diagrams of type J one obtains a functor
- lim : CJ → C
which sends each diagram to its limit.
Dually, the colimit of diagram D is a universal cone from D. If the colimit exists for all diagrams of type J one has a functor
- colim : CJ → C
which sends each diagram to its colimit.
Commutative diagrams
Diagrams and functor categories are often visualized by commutative diagrams, particularly if the index category is a finite poset category with few elements: one draws a commutative diagram with a node for every object in the index category, and an arrow for a generating set of morphisms, omitting identity maps and morphisms that can be expressed as compositions. The commutativity corresponds to the uniqueness of a map between two objects in a poset category. Conversely, every commutative diagram represents a diagram (a functor from a poset index category) in this way.Not every diagram commutes, as not every index category is a poset category:
most simply, the diagram of a single object with an endomorphism (
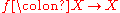), or with two parallel arrows (; 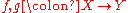) need not commute. Further, diagrams may be impossible (because infinite) or messy (because many objects or morphisms) to draw; however, schematic commutative diagrams (for subcategories of the index category, or with ellipses, such as for a directed system) are used to clarify such complex diagrams.Examples
- Indexed familyIndexed familyIn mathematics, an indexed family is a collection of values that are associated with indexes. For example, a family of real numbers, indexed by the integers is a collection of real numbers, where each integer is associated with one of the real numbers....
- Direct system
- Inverse systemInverse systemIn mathematics, an inverse system in a category C is a functor from a small cofiltered category I to C. An inverse system is sometimes called a pro-object in C. The dual concept is a direct system.-The category of inverse systems:...
- SpanSpan (category theory)A span, in category theory, is a generalization of the notion of relation between two objects of a category. When the category has all pullbacks , spans can be considered as morphisms in a category of fractions....
- Cospan