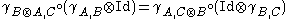Braided monoidal category
Encyclopedia
In mathematics
, a commutativity constraint on a monoidal category
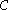is a natural isomorphism 
from 
to 
, where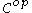 
is the category with the opposite tensor product. Explicitly, 
is a choice of isomorphism
for each pair of objects A and B which form a "natural family." In particular, to have a commutativity constraint, one must have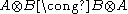
for all pairs of objects 
.
A braided monoidal category is a monoidal category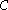
equipped with a commutativity constraint 
which satisfies the hexagon axiom (see below). The term braided comes from the fact that the braid group
plays an important role in the theory of braided monoidal categories. Partly for this reason, braided monoidal categories and various related notions are important in the theory of knot invariants.
Alternatively, a braided monoidal category can be seen as a tricategory
with one 0-cell and one 1-cell.
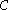along with the commutativity constraint 
to be called a braided monoidal category, the
following hexagonal diagrams must commute for all objects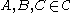
. Here 
is the associativity isomorphism coming from the monoidal structure
on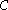
:
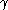along with the maps 
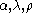coming from the monoidal structure on the category 
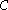, satisfy various coherence condition
s which state that various compositions of structure maps are equal. In particular:
as maps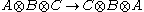
. Here we have left out the associator maps.
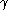also satisfies 
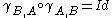for all pairs of objects 
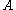and 
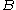. In this case the action of 
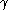on an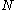 
-fold tensor product factors through the symmetric group
, and it has a good notion of quantum trace and co-quantum trace. Ribbon categories are particularly useful in constructing knot invariants
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a commutativity constraint on a monoidal category
Monoidal category
In mathematics, a monoidal category is a category C equipped with a bifunctorwhich is associative, up to a natural isomorphism, and an object I which is both a left and right identity for ⊗, again up to a natural isomorphism...
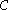is a natural isomorphism from to , where 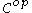is the category with the opposite tensor product. Explicitly, 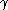is a choice of isomorphismfor each pair of objects A and B which form a "natural family." In particular, to have a commutativity constraint, one must have
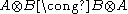for all pairs of objects .A braided monoidal category is a monoidal category
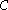equipped with a commutativity constraint which satisfies the hexagon axiom (see below). The term braided comes from the fact that the braid groupBraid group
In mathematics, the braid group on n strands, denoted by Bn, is a group which has an intuitive geometrical representation, and in a sense generalizes the symmetric group Sn. Here, n is a natural number; if n > 1, then Bn is an infinite group...
plays an important role in the theory of braided monoidal categories. Partly for this reason, braided monoidal categories and various related notions are important in the theory of knot invariants.
Alternatively, a braided monoidal category can be seen as a tricategory
Tricategory
In mathematics, a tricategory is a kind of structure of category theory studied in higher-dimensional category theory.Whereas a weak 2-category is said to be a bicategory [Benabou 1967], a weak 3-category is said to be a tricategory .Tetracategories are the corresponding notion in dimension four...
with one 0-cell and one 1-cell.
The hexagon axiom
For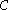 along with the commutativity constraint to be called a braided monoidal category, thefollowing hexagonal diagrams must commute for all objects
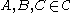. Here is the associativity isomorphism coming from the monoidal structureMonoidal category
In mathematics, a monoidal category is a category C equipped with a bifunctorwhich is associative, up to a natural isomorphism, and an object I which is both a left and right identity for ⊗, again up to a natural isomorphism...
on
:
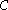Coherence
It can be shown that the natural isomorphism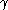 along with the maps 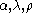coming from the monoidal structure on the category 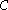, satisfy various coherence conditionCoherence condition
In mathematics, and particularly category theory a coherence condition is a collection of conditions requiring that various compositions of elementary morphisms are equal...
s which state that various compositions of structure maps are equal. In particular:
- The braiding commutes with the units. That is, the following diagram commutes:
- The action of
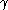on an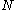 
-fold tensor product factors through the braid groupBraid groupIn mathematics, the braid group on n strands, denoted by Bn, is a group which has an intuitive geometrical representation, and in a sense generalizes the symmetric group Sn. Here, n is a natural number; if n > 1, then Bn is an infinite group...
. In particular,
as maps
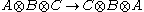. Here we have left out the associator maps.Variations
There are several variants of braided monoidal categories that are used in various contexts. See, for example, the expository paper of Savage (2009) for an explanation of symmetric and coboundary monoidal categories, and the book by Chari and Pressley (1995) for ribbon categories.Symmetric monoidal categories
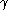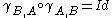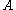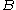A braided monoidal category is called symmetric if also satisfies for all pairs of objects and . In this case the action of 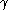on an 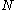-fold tensor product factors through the symmetric groupSymmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
Ribbon categories
A braided monoidal category is a ribbon category if it is rigidRigid category
In category theory, a branch of mathematics, a rigid category is a monoidal category where every object is rigid, that is, has a dual X* and a morphism 1 → X ⊗ X* satisfying natural conditions. The category is called right rigid or left rigid according to whether it has right duals or...
, and it has a good notion of quantum trace and co-quantum trace. Ribbon categories are particularly useful in constructing knot invariants
Coboundary monoidal categories
Sometimes categories are assumed to have n-ary monoidal products for all finite n (in particular n>2), diminishing the role of associator morphisms. In such categories, the following variant is used, where the hexagon axiom is replaced by the two conditions:-
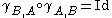for all pairs of objects 
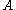and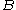 
.
Examples
- The category of representations of a group (or a lie algebra) is a symmetric monoidal category where
.
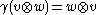- The category of representations of a quantized universal enveloping algebraQuantum groupIn mathematics and theoretical physics, the term quantum group denotes various kinds of noncommutative algebra with additional structure. In general, a quantum group is some kind of Hopf algebra...
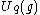is a braided monoidal category, where 
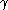is constructed using the Universal R-matrix. In fact, this example is a ribbon category as well.
Applications
- knot invariants.
- Symmetric closed monoidal categoriesClosed monoidal categoryIn mathematics, especially in category theory, aclosed monoidal category is a context where we can take tensor products of objects and also form 'mapping objects'. A classic example is the category of sets, Set, where the tensor product of sets A and B is the usual cartesian product A \times B, and...
are used in denotational models of linear logicLinear logicLinear logic is a substructural logic proposed by Jean-Yves Girard as a refinement of classical and intuitionistic logic, joining the dualities of the former with many of the constructive properties of the latter...
and linear types.
External links
- John Baez (1999), An introduction to braided monoidal categories, This week's finds in mathematical physics 137.