External ray
Encyclopedia
An external ray is a curve
that runs from infinity toward a Julia
or Mandelbrot set
.
This curve is only sometimes a half-line ( ray ) but is called ray because it is image of ray.
External rays are used in complex analysis
, particularly in complex dynamics
and geometric function theory
,
and Hubbard
's study of the Mandelbrot set
s on dynamical plane are often called dynamic rays.
External rays of the Mandelbrot set (and similar one-dimensional connectedness loci
) on parameter plane are called parameter rays.
, full, connected
subset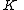 of the complex plane
of the complex plane
as :
External rays together with equipotential lines of Douady-Hubbard potential ( level sets) form a new polar coordinate system
for exterior
( complement
) of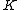 .
.
In other words the external rays define vertical foliation
which is orthogonal to horizontal foliation defined by the level sets of potential.
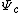 be the mapping from the complement (exterior)
be the mapping from the complement (exterior)
of the closed unit disk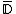 to the complement of the filled Julia set
to the complement of the filled Julia set
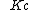 .
.
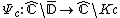
and Boettcher map (function)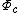 , which is uniformizing
, which is uniformizing
map of basin of attraction of infinity , because it conjugates complement of the filled Julia set
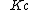 and the complement (exterior)
and the complement (exterior)
of the closed unit disk
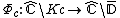
where :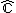 denotes the extended complex plane
denotes the extended complex plane
Boettcher map is an isomorphism
is an isomorphism
:

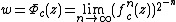
where :

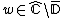
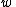 is a Boettcher coordinate
is a Boettcher coordinate
 The external ray of angle
The external ray of angle 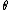 is:
is:

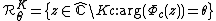

 Let
Let 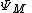 be the mapping from the complement (exterior)
be the mapping from the complement (exterior)
of the closed unit disk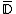 to the complement of the Mandelbrot set
to the complement of the Mandelbrot set
 .
.
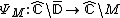
and Boettcher map (function)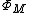 , which is uniformizing
, which is uniformizing
map of complement of Mandelbrot set , because it conjugates
complement of the Mandelbrot set
 and the complement (exterior)
and the complement (exterior)
of the closed unit disk
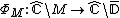
it can be normalized so that :
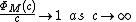
where :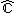 denotes the extended complex plane
denotes the extended complex plane
Jungreis function is the inverse of uniformizing
is the inverse of uniformizing
map :

In the case of complex quadratic polynomial
one can compute this map using Laurent series
about infinity

where
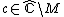
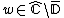
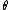 is:
is:
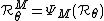
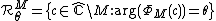
Definition of
Douady and Hubbard define:

so external angle of point of parameter plane is equal to external angle of point
of parameter plane is equal to external angle of point  of dynamical plane
of dynamical plane
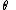 is named external angle ( argument ).
is named external angle ( argument ).
Principal value
of external angles are measured in turns
modulo
1
1 turn
= 360 degrees
= 2 * Pi radian
s
Compare different types of angles :
maps ( for example exponential
) infinity is not a fixed point but an essential singularity
and there is no Boettcher isomorphism.
Here dynamic ray is defined as a curve :
Mandelbrot set
for complex quadratic polynomial
with parameter rays of root points
Parameter space of the complex exponential family f(z)=exp(z)+c
. Eight parameter rays landing at this parameter are drawn in black.


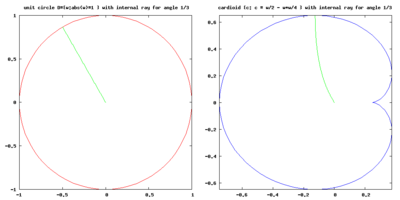 internal ray of main cardioid of angle 1/3:
internal ray of main cardioid of angle 1/3:
starts from center of main cardioid c=0
ends in the root point of period 3 component
which is the landing point of parameter (external) rays of angles 1/7 and 2/7
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
that runs from infinity toward a Julia
Julia set
In the context of complex dynamics, a topic of mathematics, the Julia set and the Fatou set are two complementary sets defined from a function...
or Mandelbrot set
Mandelbrot set
The Mandelbrot set is a particular mathematical set of points, whose boundary generates a distinctive and easily recognisable two-dimensional fractal shape...
.
This curve is only sometimes a half-line ( ray ) but is called ray because it is image of ray.
External rays are used in complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, particularly in complex dynamics
Complex dynamics
Complex dynamics is the study of dynamical systems defined by iteration of functions on complex number spaces. Complex analytic dynamics is the study of the dynamics of specifically analytic functions.-Techniques:*General** Montel's theorem...
and geometric function theory
Geometric function theory
Geometric function theory is the study of geometric properties of analytic functions. A fundamental result in the theory is the Riemann mapping theorem.-Riemann mapping theorem:...
,
History
External rays were introduced in DouadyAdrien Douady
Adrien Douady was a French mathematician.He was a student of Henri Cartan at the Ecole Normale Supérieure, and initially worked in homological algebra. His thesis concerned deformations of complex analytic spaces...
and Hubbard
John H. Hubbard
John Hamal Hubbard was born on October 6 or 7, 1945 . He is an American mathematician who is currently a professor at Cornell University and the Université de Provence. He is well known for the mathematical contributions he made with Adrien Douady in the field of complex dynamics, including a study...
's study of the Mandelbrot set
Mandelbrot set
The Mandelbrot set is a particular mathematical set of points, whose boundary generates a distinctive and easily recognisable two-dimensional fractal shape...
Notation
External rays of (connected) Julia setJulia set
In the context of complex dynamics, a topic of mathematics, the Julia set and the Fatou set are two complementary sets defined from a function...
s on dynamical plane are often called dynamic rays.
External rays of the Mandelbrot set (and similar one-dimensional connectedness loci
Connectedness locus
In one-dimensional complex dynamics, the connectedness locus in a parameter space of polynomials or rational functions consists of those parameters for which the corresponding Julia set is connected....
) on parameter plane are called parameter rays.
Dynamical plane = z-plane
External rays are associated to a compactCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
, full, connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
subset
 of the complex plane
of the complex planeComplex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
as :
- the images of radial rays under the Riemann map of the complement of
- the gradient lines of the Green's functionGreen's functionIn mathematics, a Green's function is a type of function used to solve inhomogeneous differential equations subject to specific initial conditions or boundary conditions...
of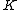
- field lineField lineA field line is a locus that is defined by a vector field and a starting location within the field. Field lines are useful for visualizing vector fields, which are otherwise hard to depict...
s of Douady-Hubbard potential - an integral curve of the gradient vector field of the Green's functionGreen's functionIn mathematics, a Green's function is a type of function used to solve inhomogeneous differential equations subject to specific initial conditions or boundary conditions...
on neighborhood of infinity
External rays together with equipotential lines of Douady-Hubbard potential ( level sets) form a new polar coordinate system
Polar coordinate system
In mathematics, the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a fixed point and an angle from a fixed direction....
for exterior
Exterior (topology)
In topology, the exterior of a subset S of a topological space X is the union of all open sets of X which are disjoint from S. It is itself an open set and is disjoint from S...
( complement
Complement (set theory)
In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
) of
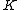 .
.In other words the external rays define vertical foliation
Foliation
In mathematics, a foliation is a geometric device used to study manifolds, consisting of an integrable subbundle of the tangent bundle. A foliation looks locally like a decomposition of the manifold as a union of parallel submanifolds of smaller dimension....
which is orthogonal to horizontal foliation defined by the level sets of potential.
Uniformization
Let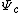 be the mapping from the complement (exterior)
be the mapping from the complement (exterior)Complement (set theory)
In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
of the closed unit disk
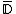 to the complement of the filled Julia set
to the complement of the filled Julia setFilled Julia set
The filled-in Julia set \ K of a polynomial \ f is a Julia set and its interior.-Formal definition:The filled-in Julia set \ K of a polynomial \ f is defined as the set of all points z\, of dynamical plane that have bounded orbit with respect to \ f...
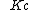 .
.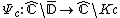
and Boettcher map (function)
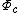 , which is uniformizing
, which is uniformizingUniformization theorem
In mathematics, the uniformization theorem says that any simply connected Riemann surface is conformally equivalent to one of the three domains: the open unit disk, the complex plane, or the Riemann sphere. In particular it admits a Riemannian metric of constant curvature...
map of basin of attraction of infinity , because it conjugates complement of the filled Julia set
Filled Julia set
The filled-in Julia set \ K of a polynomial \ f is a Julia set and its interior.-Formal definition:The filled-in Julia set \ K of a polynomial \ f is defined as the set of all points z\, of dynamical plane that have bounded orbit with respect to \ f...
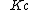 and the complement (exterior)
and the complement (exterior)Complement (set theory)
In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
of the closed unit disk
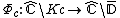
where :
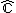 denotes the extended complex plane
denotes the extended complex planeRiemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
Boettcher map
 is an isomorphism
is an isomorphismIsomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
:

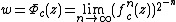
where :

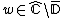
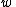 is a Boettcher coordinate
is a Boettcher coordinateFormal definition of dynamic ray

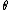 is:
is:
- the image under
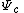 of straight lines
of straight lines 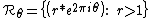

- set of points of exterior of filled-in Julia set with the same external angle
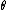
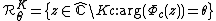
Uniformization


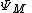 be the mapping from the complement (exterior)
be the mapping from the complement (exterior)Complement (set theory)
In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
of the closed unit disk
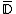 to the complement of the Mandelbrot set
to the complement of the Mandelbrot setMandelbrot set
The Mandelbrot set is a particular mathematical set of points, whose boundary generates a distinctive and easily recognisable two-dimensional fractal shape...
 .
.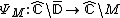
and Boettcher map (function)
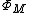 , which is uniformizing
, which is uniformizingUniformization theorem
In mathematics, the uniformization theorem says that any simply connected Riemann surface is conformally equivalent to one of the three domains: the open unit disk, the complex plane, or the Riemann sphere. In particular it admits a Riemannian metric of constant curvature...
map of complement of Mandelbrot set , because it conjugates
Topological conjugation
In mathematics, two functions are said to be topologically conjugate to one another if there exists a homeomorphism that will conjugate the one into the other...
complement of the Mandelbrot set
Mandelbrot set
The Mandelbrot set is a particular mathematical set of points, whose boundary generates a distinctive and easily recognisable two-dimensional fractal shape...
 and the complement (exterior)
and the complement (exterior)Complement (set theory)
In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
of the closed unit disk
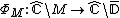
it can be normalized so that :
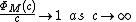
where :
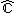 denotes the extended complex plane
denotes the extended complex planeRiemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
Jungreis function
 is the inverse of uniformizing
is the inverse of uniformizingUniformization theorem
In mathematics, the uniformization theorem says that any simply connected Riemann surface is conformally equivalent to one of the three domains: the open unit disk, the complex plane, or the Riemann sphere. In particular it admits a Riemannian metric of constant curvature...
map :

In the case of complex quadratic polynomial
Complex quadratic polynomial
A complex quadratic polynomial is a quadratic polynomial whose coefficients are complex numbers.-Forms:When the quadratic polynomial has only one variable , one can distinguish its 4 main forms:...
one can compute this map using Laurent series
Laurent series
In mathematics, the Laurent series of a complex function f is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where...
about infinity
Infinity
Infinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...

where
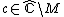
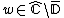
Formal definition of parameter ray
The external ray of angle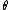 is:
is:
- the image under
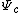 of straight lines
of straight lines 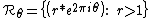
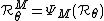
- set of points of exterior of Mandelbrot set with the same external angle
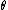
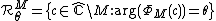
Definition of 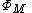
Douady and Hubbard define:
so external angle of point
 of parameter plane is equal to external angle of point
of parameter plane is equal to external angle of point  of dynamical plane
of dynamical planeExternal angle
Angle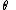 is named external angle ( argument ).
is named external angle ( argument ).Principal value
Principal value
In considering complex multiple-valued functions in complex analysis, the principal values of a function are the values along one chosen branch of that function, so it is single-valued.-Motivation:...
of external angles are measured in turns
Turn (geometry)
A turn is an angle equal to a 360° or 2 radians or \tau radians. A turn is also referred to as a revolution or complete rotation or full circle or cycle or rev or rot....
modulo
Modulo operation
In computing, the modulo operation finds the remainder of division of one number by another.Given two positive numbers, and , a modulo n can be thought of as the remainder, on division of a by n...
1
1 turn
Turn (geometry)
A turn is an angle equal to a 360° or 2 radians or \tau radians. A turn is also referred to as a revolution or complete rotation or full circle or cycle or rev or rot....
= 360 degrees
Degree (angle)
A degree , usually denoted by ° , is a measurement of plane angle, representing 1⁄360 of a full rotation; one degree is equivalent to π/180 radians...
= 2 * Pi radian
Radian
Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
s
Compare different types of angles :
- external ( point of set's exterior )
- internal ( point of component's interior )
- plain ( argument of complex numberArg (mathematics)In mathematics, arg is a function operating on complex numbers . It gives the angle between the line joining the point to the origin and the positive real axis, shown as in figure 1 opposite, known as an argument of the point In mathematics, arg is a function operating on complex numbers...
)
| external angle | internal angle | plain angle | |
|---|---|---|---|
| parameter plane |  |
 |
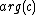 |
| dynamic plane | 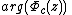 |
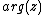 |
|
Computation of external argument
- argument of Böttcher coordinate as an external argument
-
- kneading sequence as a binary expansion of external argument
Transcendental maps
For transcendentalTranscendental function
A transcendental function is a function that does not satisfy a polynomial equation whose coefficients are themselves polynomials, in contrast to an algebraic function, which does satisfy such an equation...
maps ( for example exponential
Exponential map (discrete dynamical systems)
In the theory of dynamical systems, the exponential map can be used as the evolution function of the discrete nonlinear dynamical system.The family of exponential functions is called exponential family....
) infinity is not a fixed point but an essential singularity
Essential singularity
In complex analysis, an essential singularity of a function is a "severe" singularity near which the function exhibits extreme behavior.The category essential singularity is a "left-over" or default group of singularities that are especially unmanageable: by definition they fit into neither of the...
and there is no Boettcher isomorphism.
Here dynamic ray is defined as a curve :
- connecting a point in an escaping setEscaping setIn mathematics, and particularly complex dynamics, the escaping set of an entire function ƒ consists of all points that tend to infinity under the repeated iteration of ƒ....
and infinity - lying in an escaping setEscaping setIn mathematics, and particularly complex dynamics, the escaping set of an entire function ƒ consists of all points that tend to infinity under the repeated iteration of ƒ....
Images
Dynamic raysMandelbrot set
Mandelbrot set
The Mandelbrot set is a particular mathematical set of points, whose boundary generates a distinctive and easily recognisable two-dimensional fractal shape...
for complex quadratic polynomial
Complex quadratic polynomial
A complex quadratic polynomial is a quadratic polynomial whose coefficients are complex numbers.-Forms:When the quadratic polynomial has only one variable , one can distinguish its 4 main forms:...
with parameter rays of root points
Parameter space of the complex exponential family f(z)=exp(z)+c
Exponential map (discrete dynamical systems)
In the theory of dynamical systems, the exponential map can be used as the evolution function of the discrete nonlinear dynamical system.The family of exponential functions is called exponential family....
. Eight parameter rays landing at this parameter are drawn in black.

Center, root, external and internal ray


starts from center of main cardioid c=0
ends in the root point of period 3 component
which is the landing point of parameter (external) rays of angles 1/7 and 2/7
Programs that can draw external rays
- Mandel - program by Wolf Jung written in C++C++C++ is a statically typed, free-form, multi-paradigm, compiled, general-purpose programming language. It is regarded as an intermediate-level language, as it comprises a combination of both high-level and low-level language features. It was developed by Bjarne Stroustrup starting in 1979 at Bell...
using Qt with source codeSource codeIn computer science, source code is text written using the format and syntax of the programming language that it is being written in. Such a language is specially designed to facilitate the work of computer programmers, who specify the actions to be performed by a computer mostly by writing source...
available under the GNU General Public LicenseGNU General Public LicenseThe GNU General Public License is the most widely used free software license, originally written by Richard Stallman for the GNU Project.... - Java applets by Evgeny Demidov ( code of mndlbrot::turn function by Wolf Jung has been ported to Java ) with free source codeSource codeIn computer science, source code is text written using the format and syntax of the programming language that it is being written in. Such a language is specially designed to facilitate the work of computer programmers, who specify the actions to be performed by a computer mostly by writing source...
- OTIS by Tomoki KAWAHIRA - Java appletJava appletA Java applet is an applet delivered to users in the form of Java bytecode. Java applets can run in a Web browser using a Java Virtual Machine , or in Sun's AppletViewer, a stand-alone tool for testing applets...
without source codeSource codeIn computer science, source code is text written using the format and syntax of the programming language that it is being written in. Such a language is specially designed to facilitate the work of computer programmers, who specify the actions to be performed by a computer mostly by writing source... - Spider XView program by Yuval Fisher
- YABMP by Prof. Eugene Zaustinsky for DOSDOSDOS, short for "Disk Operating System", is an acronym for several closely related operating systems that dominated the IBM PC compatible market between 1981 and 1995, or until about 2000 if one includes the partially DOS-based Microsoft Windows versions 95, 98, and Millennium Edition.Related...
without source codeSource codeIn computer science, source code is text written using the format and syntax of the programming language that it is being written in. Such a language is specially designed to facilitate the work of computer programmers, who specify the actions to be performed by a computer mostly by writing source... - DH_Drawer by Arnaud Chéritat written for Windows 95 without source codeSource codeIn computer science, source code is text written using the format and syntax of the programming language that it is being written in. Such a language is specially designed to facilitate the work of computer programmers, who specify the actions to be performed by a computer mostly by writing source...
- Linas Vepstas C programs for LinuxLinuxLinux is a Unix-like computer operating system assembled under the model of free and open source software development and distribution. The defining component of any Linux system is the Linux kernel, an operating system kernel first released October 5, 1991 by Linus Torvalds...
consoleCommand-line interfaceA command-line interface is a mechanism for interacting with a computer operating system or software by typing commands to perform specific tasks...
with source codeSource codeIn computer science, source code is text written using the format and syntax of the programming language that it is being written in. Such a language is specially designed to facilitate the work of computer programmers, who specify the actions to be performed by a computer mostly by writing source... - Program Julia by Curtis T McMullen written in C and Linux commands for C shellC shellThe C shell is a Unix shell that was created by Bill Joy while a graduate student at University of California, Berkeley in the late 1970s. It has been distributed widely, beginning with the 2BSD release of the BSD Unix system that Joy began distributing in 1978...
consoleCommand-line interfaceA command-line interface is a mechanism for interacting with a computer operating system or software by typing commands to perform specific tasks...
with source codeSource codeIn computer science, source code is text written using the format and syntax of the programming language that it is being written in. Such a language is specially designed to facilitate the work of computer programmers, who specify the actions to be performed by a computer mostly by writing source... - mjwinq program by Matjaz Erat written in delphi/windows without source codeSource codeIn computer science, source code is text written using the format and syntax of the programming language that it is being written in. Such a language is specially designed to facilitate the work of computer programmers, who specify the actions to be performed by a computer mostly by writing source...
( For the external rays it uses the methods from quad.c in julia.tar by Curtis T McMullen) - RatioField by Gert Buschmann, for windows with PascalPascal (programming language)Pascal is an influential imperative and procedural programming language, designed in 1968/9 and published in 1970 by Niklaus Wirth as a small and efficient language intended to encourage good programming practices using structured programming and data structuring.A derivative known as Object Pascal...
source code for Dev-Pascal 1.9.2 (with Free PascalFree PascalFree Pascal Compiler is a free Pascal and Object Pascal compiler.In addition to its own Object Pascal dialect, Free Pascal supports, to varying degrees, the dialects of several other compilers, including those of Turbo Pascal, Delphi, and some historical Macintosh compilers...
compiler ) - Mandelbrot program by Milan Va, written in Delphi with source code
- Power MANDELZOOM by Robert Munafo
- ruff by Claude Heiland-Allen
See also
- external rays of Misiurewicz pointMisiurewicz pointA Misiurewicz point is a parameter in the Mandelbrot set for which the critical point is strictly preperiodic . By analogy, the term Misiurewicz point is also used for parameters in a Multibrot set where the unique critical point is strictly preperiodic...
- Orbit portraitOrbit portraitIn mathematics, an orbit portrait is a combinatorial tool used in complex dynamics for understanding the behavior of one-complex dimensional quadratic maps.In simple words one can say that it is :...
- Periodic points of complex quadratic mappingsPeriodic points of complex quadratic mappingsThis article describes periodic points of some complex quadratic maps. A map is a formula for computing a value of a variable based on its own previous value or values; a quadratic map is one that involves the previous value raised to the powers one and two; and a complex map is one in which the...
- Prouhet-Thue-Morse constantProuhet-Thue-Morse constantIn mathematics, the Prouhet–Thue–Morse constant, named for Eugène Prouhet, Axel Thue, and Marston Morse, is the number—denoted by \tau—whose binary expansion .01101001100101101001011001101001... is given by the Thue–Morse sequence...
- Carathéodory's theoremCarathéodory's theorem (conformal mapping)In mathematical complex analysis, Carathéodory's theorem, proved by , states that if U is a simply connected open subset of the complex plane C, whose boundary is a Jordan curve Γ then the Riemann map...
- Field lines of Julia sets