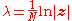Multibrot set
Encyclopedia
In mathematics, a multibrot set is the set of values in the complex plane
whose absolute value remains below some finite value throughout iterations by a member of the general monic univariate polynomial family of recursion
s
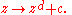
where d ≥ 2. The exponent d may be further generalized to negative and fractional values.
is the classic Mandelbrot set
from which the name is derived.
The sets for other values of d also show fractal images when they are plotted on the complex plane.
Each of the examples of various powers d shown below is plotted to the same scale. Values of c belonging to the set are black. Values of c that have unbounded value under recursion, and thus do not belong in the set, are plotted in different colours, that show as contours, depending on the number of recursions that caused a value to exceed a fixed magnitude in the Escape Time algorithm.
, as shown by the example below. The Lyapunov exponent is the error growth-rate of a given sequence. First calculate the iteration sequence with N iterations, then calculate the exponent as
and if the exponent is negative the sequence is stable. The white pixels in the picture are the parameters c for which the exponent is positive aka unstable. The colours show the periods of the cycles which the orbits are attracted to. All points colored dark-blue (outside) are attracted by a fixed point, all points in the middle (lighter blue) are attracted by a period 2 cycle and so on.


For each pixel on the screen do:
{
x = x0 = x co-ordinate of pixel
y = y0 = y co-ordinate of pixel
iteration = 0
max_iteration = 1000
while ( x*x + y*y <= (2*2) AND iteration < max_iteration )
{
/* INSERT CODE(S)FOR Z^d FROM TABLE BELOW */
iteration = iteration + 1
}
if ( iteration max_iteration )
then
colour = black
else
colour = iteration
plot(x0,y0,colour)
}
The complex value z has coordinates (x,y) on the complex plane and is raised to various powers inside the iteration loop by codes shown in this table. Powers not shown in the table can be obtained by concatenating the codes shown.
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
whose absolute value remains below some finite value throughout iterations by a member of the general monic univariate polynomial family of recursion
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
s
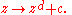
where d ≥ 2. The exponent d may be further generalized to negative and fractional values.
Examples
The case ofis the classic Mandelbrot set
Mandelbrot set
The Mandelbrot set is a particular mathematical set of points, whose boundary generates a distinctive and easily recognisable two-dimensional fractal shape...
from which the name is derived.
The sets for other values of d also show fractal images when they are plotted on the complex plane.
Each of the examples of various powers d shown below is plotted to the same scale. Values of c belonging to the set are black. Values of c that have unbounded value under recursion, and thus do not belong in the set, are plotted in different colours, that show as contours, depending on the number of recursions that caused a value to exceed a fixed magnitude in the Escape Time algorithm.
Positive powers
The example is the original Mandelbrot set. The examples for are often called Multibrot sets. These sets include the origin and have fractal perimeters, with rotational symmetry. |
 |
 |
 |
 |
Negative powers
When d is negative the set surrounds but does not include the origin. There is interesting complex behaviour in the contours between the set and the origin, in a star-shaped area with rotational symmetry. The sets appear to have a circular perimeter, however this is just an artifact of the fixed maximum radius allowed by the Escape Time algorithm, and is not a limit of the sets that actually extend in all directions to infinity. |
 |
 |
 |
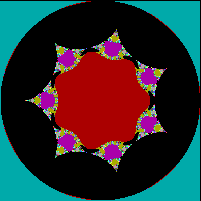 |
Rendering images
All the above images are rendered using an Escape Time algorithm that identifies points outside the set in a simple way. Much greater fractal detail is revealed by plotting the Lyapunov exponentLyapunov exponent
In mathematics the Lyapunov exponent or Lyapunov characteristic exponent of a dynamical system is a quantity that characterizes the rate of separation of infinitesimally close trajectories...
, as shown by the example below. The Lyapunov exponent is the error growth-rate of a given sequence. First calculate the iteration sequence with N iterations, then calculate the exponent as
and if the exponent is negative the sequence is stable. The white pixels in the picture are the parameters c for which the exponent is positive aka unstable. The colours show the periods of the cycles which the orbits are attracted to. All points colored dark-blue (outside) are attracted by a fixed point, all points in the middle (lighter blue) are attracted by a period 2 cycle and so on.


For each pixel on the screen do:
{
x = x0 = x co-ordinate of pixel
y = y0 = y co-ordinate of pixel
iteration = 0
max_iteration = 1000
while ( x*x + y*y <= (2*2) AND iteration < max_iteration )
{
/* INSERT CODE(S)FOR Z^d FROM TABLE BELOW */
iteration = iteration + 1
}
if ( iteration max_iteration )
then
colour = black
else
colour = iteration
plot(x0,y0,colour)
}
The complex value z has coordinates (x,y) on the complex plane and is raised to various powers inside the iteration loop by codes shown in this table. Powers not shown in the table can be obtained by concatenating the codes shown.
| z−1 | z2 (for Mandelbrot set) | z3 | z5 |
d=x^2+y^2 | xtmp=x^2-y^2 | xtmp=x^3-3*x*y^2 | xtmp=x^5-10*x^3*y^2+5*x*y^4 |