
Pedal curve
Encyclopedia
In the differential geometry of curves
, a pedal curve is a curve
derived by construction from a given curve
(as is, for example, the involute
).
Let C be a given curve and P a fixed point (called the pedal point). At any point R on C let T be the tangent line at R. There is then a unique point X on T which is either P (in case P lies on T) or forms with P a line perpendicular
to T. The pedal curve is the set of all such X for all R on C. (The point X is called the foot of the perpendicular to T from P.)
Similarly, there is a unique point Y on the line normal to C at R so that PY is perpendicular to the normal, so PXRY is a (possibly degenerate) rectangle. The locus of points Y is called the contrapedal curve.
The orthotomic of a curve is its pedal magnified by a factor of 2 so that the center of similarity is P. This is locus of the reflection of P through the tangent line L
Draw a circle with diameter PR, then it circumscribes rectangle PXRY and XY is another diameter. The circle and the pedal are both perpendicular to XY so they are tangent at X. Hence the pedal is the envelope
of the circles with diameters PR where R lies on the curve.
The line YR is normal to the curve and the envelope of such normals is its evolute
. Therefore YR is tangent to the evolute and the point Y is the foot of the perpendicular from P to this tangent, in other words Y is on the pedal of the evolute. It follows that the contrapedal of a curve is the pedal of its evolute.
Let C′ be the curve obtained by shrinking C by a factor of 2 toward P. Then the point R′ corresponding to R is the center of the rectangle PXRY, and the tangent to C′ at R′ bisects this rectangle parallel to PY and XR. A ray of light starting from P and reflected by C′ at R' will then pass through Y. The reflected ray, when extended, is the line XY which is perpendicular to the pedal of C. The envelope of lines perpendicular to the pedal is then the envelope of reflected rays or the catacaustic of C′. This proves that the catacaustic of a curve is the evolute of its orthotomic.
As noted earlier, the circle with diameter PR is tangent to the pedal. The center of this circle is R′ which follows the curve C′. It follows that the envelope of circles through a fixed point and whose centers lie on a given curve is the orthotomic of the curve.
Let D′ be a curve congruent to C′ and let D′ roll without slipping, as in the definition of a roulette
, on C′ so that D′ is always the reflection of C′ with respect to the line to which they are mutually tangent. Then when the curves touch at R′ the point corresponding to P on the moving plane is X, and so the roulette is the pedal curve. Equivalently, the orthotomic of a curve is the roulette of the curve on its mirror image.
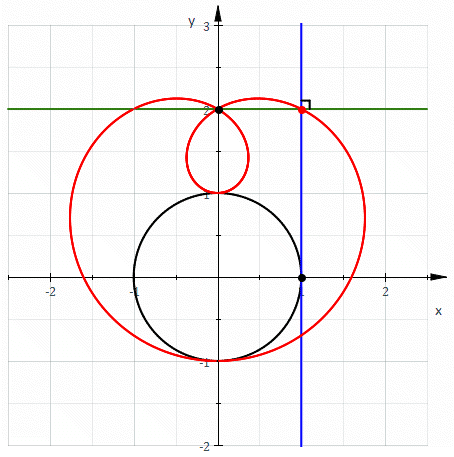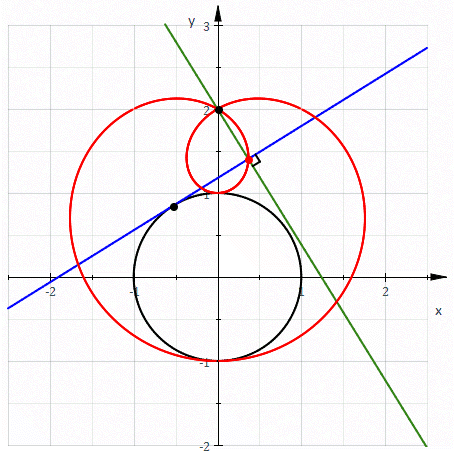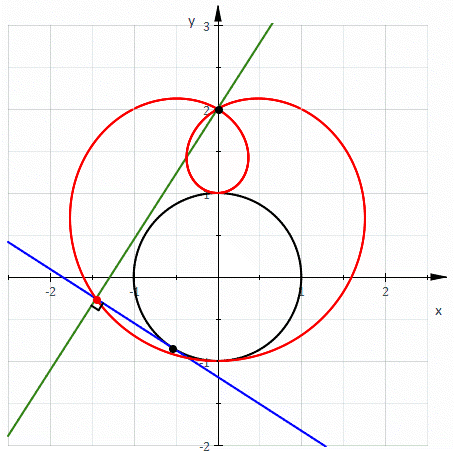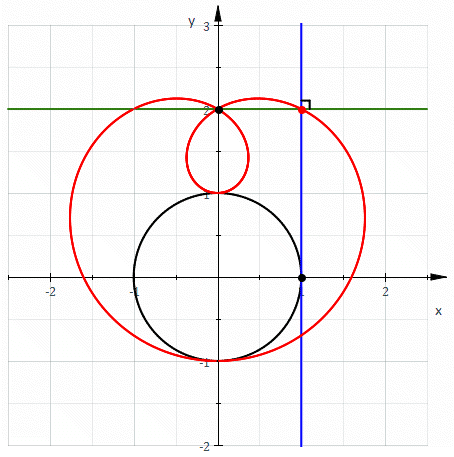 When C is a circle the above discussion shows that the following definitions of a limaçon
When C is a circle the above discussion shows that the following definitions of a limaçon
are equivalent:
We also have shown that the catacaustic of a circle is the evolute of a limaçon.
 Let
Let

be the vector for R to P and write ,
,
the tangential and normal components
of with respect to the curve.
with respect to the curve.
Then is the vector from R to X from which the position of X can be computed.
is the vector from R to X from which the position of X can be computed.
Specifically, if c is a parametrization of the curve then
parametrises the pedal curve (disregarding points where c' is zero or undefined).
For a parametrically defined curve, its pedal curve with pedal point (0;0) is defined as

The contrapedal curve is given by:
With the same pedal point, the contrapedal curve is the pedal curve of the evolute
of the given curve.
:
 and
and 

thus, the pedal curve with pedal point (x,y) is:
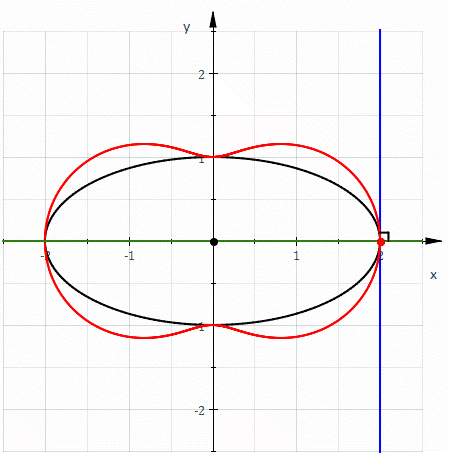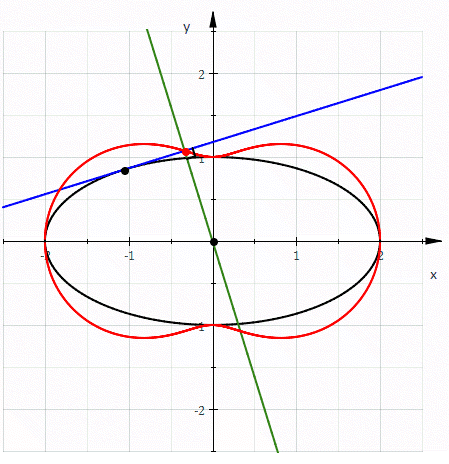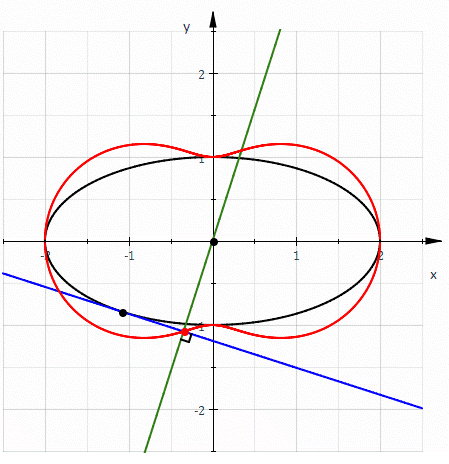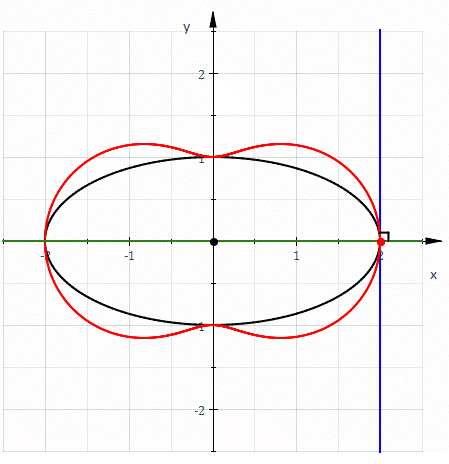
If the pedal point is at the center (i.e. (0,0)), the circle is its own pedal curve. If the pedal point is (1,0) the pedal curve is
i.e. a pedal point on the circumference gives a cardioid
.
Differential geometry of curves
Differential geometry of curves is the branch of geometry that dealswith smooth curves in the plane and in the Euclidean space by methods of differential and integral calculus....
, a pedal curve is a curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
derived by construction from a given curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
(as is, for example, the involute
Involute
In the differential geometry of curves, an involute is a curve obtained from another given curve by attaching an imaginary taut string to the given curve and tracing its free end as it is wound onto that given curve; or in reverse, unwound. It is a roulette wherein the rolling curve is a straight...
).
Let C be a given curve and P a fixed point (called the pedal point). At any point R on C let T be the tangent line at R. There is then a unique point X on T which is either P (in case P lies on T) or forms with P a line perpendicular
Perpendicular
In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...
to T. The pedal curve is the set of all such X for all R on C. (The point X is called the foot of the perpendicular to T from P.)
Similarly, there is a unique point Y on the line normal to C at R so that PY is perpendicular to the normal, so PXRY is a (possibly degenerate) rectangle. The locus of points Y is called the contrapedal curve.
The orthotomic of a curve is its pedal magnified by a factor of 2 so that the center of similarity is P. This is locus of the reflection of P through the tangent line L
Geometrical properties
Consider a right angle moving rigidly so that one leg remains on the point P and the other leg is tangent to the curve. Then the vertex of this angle is X and traces out the pedal curve. As the angle moves, its direction of motion at P is parallel to PX and its direction of motion at R is parallel to the tangent T = RX. Therefore the instant center of rotation is the intersection of the line perpendicular to PX at P and perpendicular to RX at R, and this point is Y. If follows that the tangent to the pedal at X is perpendicular to XY.Draw a circle with diameter PR, then it circumscribes rectangle PXRY and XY is another diameter. The circle and the pedal are both perpendicular to XY so they are tangent at X. Hence the pedal is the envelope
Envelope (mathematics)
In geometry, an envelope of a family of curves in the plane is a curve that is tangent to each member of the family at some point. Classically, a point on the envelope can be thought of as the intersection of two "adjacent" curves, meaning the limit of intersections of nearby curves...
of the circles with diameters PR where R lies on the curve.
The line YR is normal to the curve and the envelope of such normals is its evolute
Evolute
In the differential geometry of curves, the evolute of a curve is the locus of all its centers of curvature. Equivalently, it is the envelope of the normals to a curve....
. Therefore YR is tangent to the evolute and the point Y is the foot of the perpendicular from P to this tangent, in other words Y is on the pedal of the evolute. It follows that the contrapedal of a curve is the pedal of its evolute.
Let C′ be the curve obtained by shrinking C by a factor of 2 toward P. Then the point R′ corresponding to R is the center of the rectangle PXRY, and the tangent to C′ at R′ bisects this rectangle parallel to PY and XR. A ray of light starting from P and reflected by C′ at R' will then pass through Y. The reflected ray, when extended, is the line XY which is perpendicular to the pedal of C. The envelope of lines perpendicular to the pedal is then the envelope of reflected rays or the catacaustic of C′. This proves that the catacaustic of a curve is the evolute of its orthotomic.
As noted earlier, the circle with diameter PR is tangent to the pedal. The center of this circle is R′ which follows the curve C′. It follows that the envelope of circles through a fixed point and whose centers lie on a given curve is the orthotomic of the curve.
Let D′ be a curve congruent to C′ and let D′ roll without slipping, as in the definition of a roulette
Roulette (curve)
In the differential geometry of curves, a roulette is a kind of curve, generalizing cycloids, epicycloids, hypocycloids, trochoids, and involutes....
, on C′ so that D′ is always the reflection of C′ with respect to the line to which they are mutually tangent. Then when the curves touch at R′ the point corresponding to P on the moving plane is X, and so the roulette is the pedal curve. Equivalently, the orthotomic of a curve is the roulette of the curve on its mirror image.
Example

Limaçon
In geometry, a limaçon or limacon , also known as a limaçon of Pascal, is defined as a roulette formed when a circle rolls around the outside of a circle of equal radius. It can also be defined as the roulette formed when a circle rolls around a circle with half its radius so that the smaller...
are equivalent:
- It is the pedal of a circle.
- It is the envelope of circles whose diameters have one endpoint on a fixed point and another endpoint which follow a circle.
- It is the envelope of circles through a fixed point whose centers follow a circle.
- It is the roulette formed by a circle rolling around a circle with the same radius.
We also have shown that the catacaustic of a circle is the evolute of a limaçon.
Equations




be the vector for R to P and write
 ,
,the tangential and normal components
Tangential and normal components
In mathematics, given a vector at a point on a curve, that vector can be decomposed uniquely as a sum of two vectors, one tangent to the curve, called the tangential component of the vector, and another one perpendicular to the curve, called the normal component of the vector...
of
 with respect to the curve.
with respect to the curve.Then
 is the vector from R to X from which the position of X can be computed.
is the vector from R to X from which the position of X can be computed.Specifically, if c is a parametrization of the curve then

parametrises the pedal curve (disregarding points where c' is zero or undefined).
For a parametrically defined curve, its pedal curve with pedal point (0;0) is defined as


The contrapedal curve is given by:

With the same pedal point, the contrapedal curve is the pedal curve of the evolute
Evolute
In the differential geometry of curves, the evolute of a curve is the locus of all its centers of curvature. Equivalently, it is the envelope of the normals to a curve....
of the given curve.
| given curve | pedal point | pedal curve | contrapedal curve |
|---|---|---|---|
| line Line (mathematics) The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects... | any | point Point (geometry) In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics... | parallel line |
| circle Circle A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius.... | on circumference | cardioid Cardioid A cardioid is a plane curve traced by a point on the perimeter of a circle that is rolling around a fixed circle of the same radius. It is therefore a type of limaçon and can also be defined as an epicycloid having a single cusp... | — |
| parabola Parabola In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface... | on axis | conchoid of de Sluze Conchoid of de Sluze The conchoid of de Sluze is a family of plane curves studied in 1662 by René François Walter, baron de Sluze.The curves are defined by the polar equationr=\sec\theta+a\cos\theta \,.... | — |
| parabola Parabola In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface... | on tangent of vertex | ophiuride | — |
| parabola Parabola In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface... | focus | line | — |
| other conic section Conic section In mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2... | focus | circle | — |
| logarithmic spiral Logarithmic spiral A logarithmic spiral, equiangular spiral or growth spiral is a special kind of spiral curve which often appears in nature. The logarithmic spiral was first described by Descartes and later extensively investigated by Jacob Bernoulli, who called it Spira mirabilis, "the marvelous... | pole | congruent Congruence (geometry) In geometry, two figures are congruent if they have the same shape and size. This means that either object can be repositioned so as to coincide precisely with the other object... log spiral | congruent log spiral |
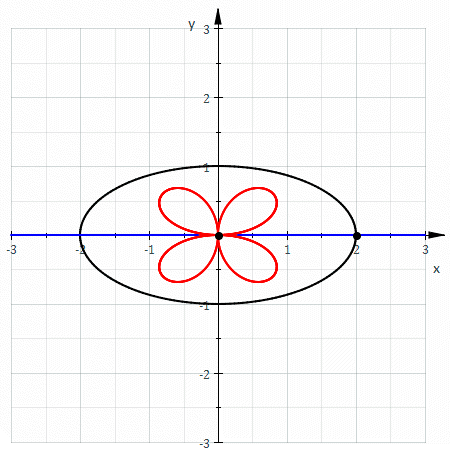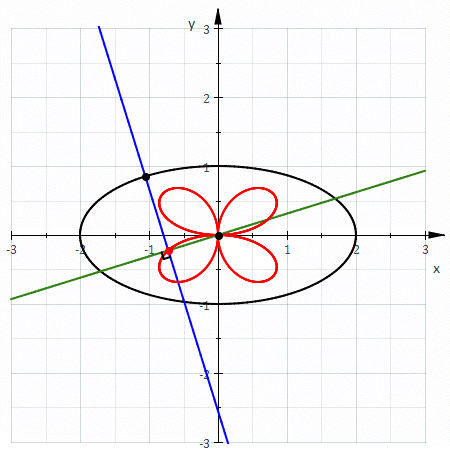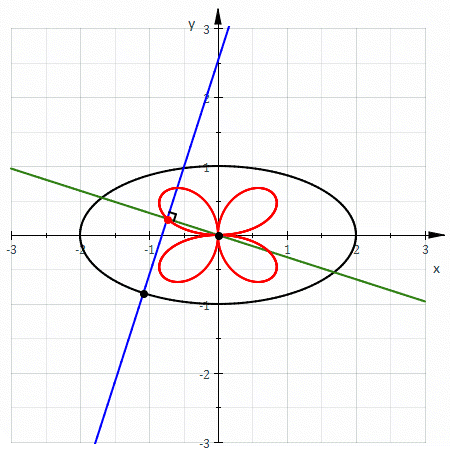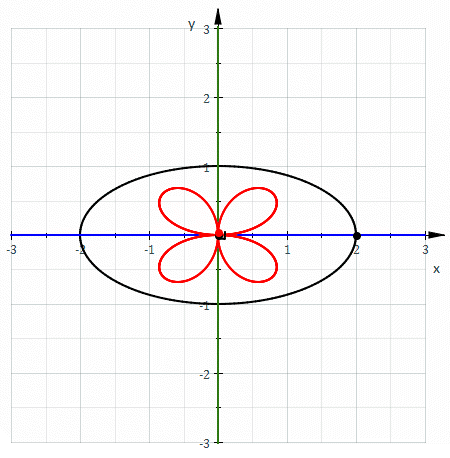
| epicycloid Epicycloid In geometry, an epicycloid is a plane curve produced by tracing the path of a chosen point of a circle — called an epicycle — which rolls without slipping around a fixed circle... hypocycloid Hypocycloid In geometry, a hypocycloid is a special plane curve generated by the trace of a fixed point on a small circle that rolls within a larger circle... | center | rose Rose (mathematics) In mathematics, a rose or rhodonea curve is a sinusoid plotted in polar coordinates. Up to similarity, thesecurves can all be expressed by a polar equation of the form\!\,r=\cos.If k is an integer, the curve will be rose shaped with... | rose |
| involute Involute In the differential geometry of curves, an involute is a curve obtained from another given curve by attaching an imaginary taut string to the given curve and tracing its free end as it is wound onto that given curve; or in reverse, unwound. It is a roulette wherein the rolling curve is a straight... of circle | center of circle | Archimedean spiral Archimedean spiral The Archimedean spiral is a spiral named after the 3rd century BC Greek mathematician Archimedes. It is the locus of points corresponding to the locations over time of a point moving away from a fixed point with a constant speed along a line which rotates with constant angular velocity... | the circle |
Example
Pedal curves of unit circleUnit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
:

 and
and 

thus, the pedal curve with pedal point (x,y) is:

If the pedal point is at the center (i.e. (0,0)), the circle is its own pedal curve. If the pedal point is (1,0) the pedal curve is

i.e. a pedal point on the circumference gives a cardioid
Cardioid
A cardioid is a plane curve traced by a point on the perimeter of a circle that is rolling around a fixed circle of the same radius. It is therefore a type of limaçon and can also be defined as an epicycloid having a single cusp...
.

