List of elementary physics formulae
Encyclopedia
The scope of the article is as follows:
1. General equations which constructed from definitions
or physical laws, or to the same status universal principles, but themselves not formulae of these types.
2. General equations which are or allow any of the following:
3. Formulae which frequently appear in physics literature, in a small addition some perhaps less common formulae.
4. Level of study is typically that of advanced school/ introductory degree level Physics, and beyond.
5. For generality, vector calculus and multivariable calculus is the main formalism; inline with complex numbers and some linear algebra (such as matrices and coordinate systems).
Only SI units and their corresponding dimensions are used; no natural/characteristic units or non-dimensional equations are included.
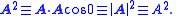 No confusion should arise by mistaking it for the cross product since the cross product of a vector with itself is always the null vector.
No confusion should arise by mistaking it for the cross product since the cross product of a vector with itself is always the null vector.
All symbols are matched as to standard closely as possible, but due to a variety of notations for any given variable, every table below has locally defined variables.
{\mathrm{d} \theta} \right ) \,\!
|-
|r = position vector of a point on the body,
W = work done by an external agent
F = force exterted by an external agent at r,
τ = torque exerted by an external agent on the body at r due to F
C = curve which the agent exerts the force/torque along
|-
|style="background: #f2f2f2"|Velocity
and acceleration
of a rotating rigid body
| rowspan="2" |
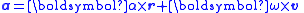
|-
|V = volume occupied by body
v = acceleration at point r about some axis
a = acceleration at point r about some axis
|-
|style="background: #f2f2f2"|Translational and angular momentum
of a rotating rigid body
| rowspan="2" |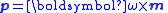
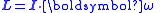
|-
|m = moment of mass at r about some axis
p = translational momentum at r about some axis
L = angular momentum about some axis
I = moment of inertia
tensor about some axis
|-
|style="background: #f2f2f2"| Coriolis acceleration and force
| rowspan="2" |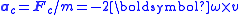
|-
|c subscripts refer to coriolis
|-
|style="background: #f2f2f2"| Euler's equations (rigid body dynamics)
|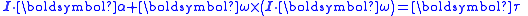
|-
|}
Equations of motion
Angular frequencies
Energy in mechanical oscillations
Corollaries of the non-relativistic Maxwell-Boltzmann distribution are below.
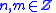 .
.
Gravitational waves
Gravitational radiation for two orbiting bodies in the low-speed limit.
The group velocity is the rate at which the wave envelope, i.e. the changes in amplitude, propagates. The wave envelope is the profile of the wave amplitudes; all transverse displacements are bound by the envelope profile.
Intuitively the wave envelope is the "global profile" of the wave, which "contains" changing "local profiles inside the global profile". Each propagates at generally different speeds determined by the important function called the Dispersion Relation
. The use of the explicit form ω(k) is standard, since the phase velocity ω/k and the group velocity dω/dk usually have convenient representations by this function.
Using complex numbers and applying the superposition to N waves of different amplitudes, frequencies, wavenumbers and phases, the general sinusoidal solution can be obtained.
The complex amplitudes are as follows.
Complex amplitude of wave n
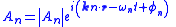
Resultant complex amplitude of all N waves
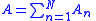
Modulus of amplitude

The transverse displacements are simply the real parts of the complex amplitudes.
Transverse displacement of wave n is
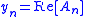
Resultant transverse displacement
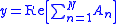
1 dimensional corollaries for two sinusoidal waves
The following may be deduced by applying the principle of superposition to two sinusoidal waves, using trigonometric identities. The angle addition and sum-to-product trigonometric formulae are useful; in more advanced work complex numbers and fourier series and transforms are used.
Weak-gravitational field relativistic equations:
\approx m \left | \mathbf{g} \right | y\,\!
|-
|style="background: #f2f2f2"| Escape speed
|rowspan="2"|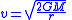
|-
| M = Mass of body (eg planet) to escape from
r = radius of body
|-
|style="background: #f2f2f2"| Orbital energy
|rowspan="2"|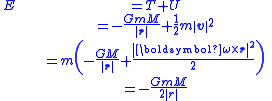
|-
| m = mass of orbiting body (eg planet)
M = mass of central body (eg star)
ω = angular velocity of orbiting mass
r = separation between centres of mass
T = kinetic energy
U = gravitational potential energy (sometimes called "gravitational binding energy" for this instance)
|-
|}
Series circuit equations
}{4 \pi \left | \mathbf{r} - \mathbf{r}' \right |} \mathrm{d}x'\mathrm{d}y'
Far-field (Fraunhofer)
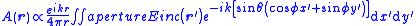
|-
| A, amplitude at position r
r' = source point in the aperture
Einc, magnitude of incident electric field at aperture
|-
|style="background: #f2f2f2"|Rayleigh's criterion
|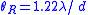
|-
|}
Probability Distributions
Angular momentum
Magnetic moments
The Hydrogen atom
Light
Common Cases
Corollaries
Continuity equation
Constitutive equation
Operator (physics)
Defining equation (physical chemistry)
Physical constant
1. General equations which constructed from definitions
Defining equation (physics)
In physics, defining equations are equations that define new quantities in terms of base quantities. This article uses the current SI system of units, not natural or characteristic units.-Treatment of vectors:There are many forms of vector notation...
or physical laws, or to the same status universal principles, but themselves not formulae of these types.
2. General equations which are or allow any of the following:
- large applicability on a specific but important topic,
- large applicability on a general topic,
- reduce to a number of idealized special cases.
3. Formulae which frequently appear in physics literature, in a small addition some perhaps less common formulae.
4. Level of study is typically that of advanced school/ introductory degree level Physics, and beyond.
5. For generality, vector calculus and multivariable calculus is the main formalism; inline with complex numbers and some linear algebra (such as matrices and coordinate systems).
Only SI units and their corresponding dimensions are used; no natural/characteristic units or non-dimensional equations are included.
Nomenclature
The short-hand notation for the square of a vector, as the dot product of a vector with itself is used: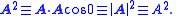 No confusion should arise by mistaking it for the cross product since the cross product of a vector with itself is always the null vector.
No confusion should arise by mistaking it for the cross product since the cross product of a vector with itself is always the null vector.All symbols are matched as to standard closely as possible, but due to a variety of notations for any given variable, every table below has locally defined variables.
Classical Mechanics
| Physical situation | Equations |
|---|---|
| General work-energy theorem (translation and rotation) |
|-
|r = position vector of a point on the body,
W = work done by an external agent
F = force exterted by an external agent at r,
τ = torque exerted by an external agent on the body at r due to F
C = curve which the agent exerts the force/torque along
|-
|style="background: #f2f2f2"|Velocity
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
and acceleration
Acceleration
In physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...
of a rotating rigid body
Rigid body
In physics, a rigid body is an idealization of a solid body of finite size in which deformation is neglected. In other words, the distance between any two given points of a rigid body remains constant in time regardless of external forces exerted on it...
| rowspan="2" |

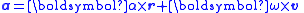
|-
|V = volume occupied by body
v = acceleration at point r about some axis
a = acceleration at point r about some axis
|-
|style="background: #f2f2f2"|Translational and angular momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
of a rotating rigid body
| rowspan="2" |
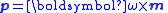
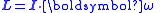
|-
|m = moment of mass at r about some axis
p = translational momentum at r about some axis
L = angular momentum about some axis
I = moment of inertia
Moment of inertia
In classical mechanics, moment of inertia, also called mass moment of inertia, rotational inertia, polar moment of inertia of mass, or the angular mass, is a measure of an object's resistance to changes to its rotation. It is the inertia of a rotating body with respect to its rotation...
tensor about some axis
|-
|style="background: #f2f2f2"| Coriolis acceleration and force
Coriolis effect
In physics, the Coriolis effect is a deflection of moving objects when they are viewed in a rotating reference frame. In a reference frame with clockwise rotation, the deflection is to the left of the motion of the object; in one with counter-clockwise rotation, the deflection is to the right...
| rowspan="2" |
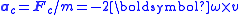
|-
|c subscripts refer to coriolis
|-
|style="background: #f2f2f2"| Euler's equations (rigid body dynamics)
|
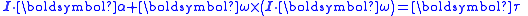
|-
|}
Mechanical oscillators
SHM, DHM, SHO, and DHO refer to simple harmonic motion, damped harmonic motion, simple harmonic oscillator and damped harmonic oscillator respectively.Equations of motion
| Physical situation | Translational equations | Angular equations |
|---|---|---|
| SHM | 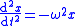 Solution: 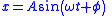 |
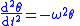 Solution:  |
| x = Transverse displacement θ = Angular displacement A = Transverse amplitude Θ = Angular amplitude |
||
| Unforced DHM | 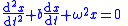 Solution (see below for ω):  Resonant frequency: 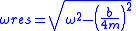 Damping rate: 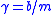 Expected lifetime of excitation: 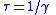 |
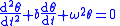 Solution:  Resonant frequency: 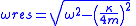 Damping rate: 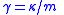 Expected lifetime of excitation: 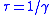 |
| b = damping constant κ = torsion constant |
||
Angular frequencies
| Physical situation | Equations |
|---|---|
| Linear undamped unforced SHO | 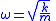 |
| k = spring constant m = mass of oscillating bob |
|
| Linear unforced DHO |  |
| k = spring constant b = Damping coefficient |
|
| Low amplitude angular SHO |  |
| I = Moment of inertia about oscillating axis κ = torsion constant |
|
| Low amplitude simple pendulum | Approximate value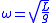 Exact value can be shown to be: 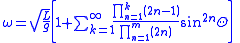 |
| L = Length of pendulum g = Gravitational acceleration Θ = Angular amplitude |
|
Energy in mechanical oscillations
| Physical situation | Equations |
|---|---|
| SHM energy | Potential energy Maximum value at x = A:  Kinetic energy 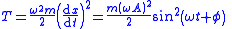 Total energy 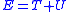 |
| T = kinetic energy U = potenial energy E = total energy |
|
| DHM energy | 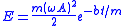 |
Fluid mechanics
| Physical situation | Equations |
|---|---|
| Fluid statics Fluid statics Fluid statics is the science of fluids at rest, and is a sub-field within fluid mechanics. The term usually refers to the mathematical treatment of the subject. It embraces the study of the conditions under which fluids are at rest in stable equilibrium... , pressure gradient Pressure gradient In atmospheric sciences , the pressure gradient is a physical quantity that describes in which direction and at what rate the pressure changes the most rapidly around a particular location. The pressure gradient is a dimensional quantity expressed in units of pressure per unit length... |
 |
| r = Position ρ = ρ(r) = Fluid density at gravitational equipotential containing r g = g(r) = Gravitational field strength at point r ∇P = Pressure gradient |
|
| Buoyancy equations | Buoyant force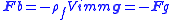 Apparent weight Apparent weight The weight in a given frame of reference is a generalized concept of weight, see the ISO definition of weight.An object's regular weight is its weight with respect to Earth...  |
| ρf = Mass density of the fluid Vimm = Immersed volume of body in fluid Fb = Buoyant force Fg = Gravitational force Wapp = Apparent weight of immersed body W = Actual weight of immersed body |
|
| Bernoulli's equation |  |
| pconstant is the total pressure at a point on a streamline |
|
| Euler equations (fluid dynamics) | 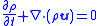 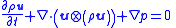 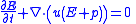 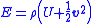 |
| ρ = fluid mass density, u is the fluid velocity Velocity In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ... vector, E = total volume energy Energy In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems... density U = internal energy Internal energy In thermodynamics, the internal energy is the total energy contained by a thermodynamic system. It is the energy needed to create the system, but excludes the energy to displace the system's surroundings, any energy associated with a move as a whole, or due to external force fields. Internal... per unit mass of fluid p = pressure Pressure Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...  denotes the tensor product denotes the tensor productTensor product In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general... |
|
| Convective acceleration | 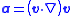 |
| Navier-stokes equations Navier-Stokes equations In physics, the Navier–Stokes equations, named after Claude-Louis Navier and George Gabriel Stokes, describe the motion of fluid substances. These equations arise from applying Newton's second law to fluid motion, together with the assumption that the fluid stress is the sum of a diffusing viscous... |
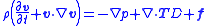 |
| TD = Deviatoric stress tensor Tensor field In mathematics, physics and engineering, a tensor field assigns a tensor to each point of a mathematical space . Tensor fields are used in differential geometry, algebraic geometry, general relativity, in the analysis of stress and strain in materials, and in numerous applications in the physical... ,  = volume density of the body force = volume density of the body forceBody force A body force is a force that acts throughout the volume of a body, in contrast to contact forces.Gravity and electromagnetic forces are examples of body forces. Centrifugal and Coriolis forces can also be viewed as body forces.This can be put into contrast to the classical definition of surface... s acting on the fluid  here is the del here is the delDel In vector calculus, del is a vector differential operator, usually represented by the nabla symbol \nabla . When applied to a function defined on a one-dimensional domain, it denotes its standard derivative as defined in calculus... operator. |
|
Kinetic theory
Ideal gas equations| Physical situation | Equations |
|---|---|
| Ideal gas law |  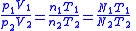 |
| p = pressure V = volume of container T = temperature n = number of moles N = number of molecules k = Boltzmann’s constant |
|
| Pressure of an ideal gas |  |
| m = mass of one molecule Mm = molar mass |
|
Phase transitions
| Physical situation | Equations |
|---|---|
| Adiabatic transition |  |
| Isothermal transition |  For an ideal gas 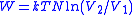 |
| Isobaric transition | p1 = p2, p = constant 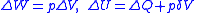 |
| Isochoric transition | V1 = V2, V = constant  |
| Adiabatic expansion |  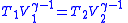 |
| Free expansion | 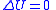 |
| Work done by an expanding gas | Process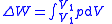 Net Work Done in Cyclic Processes 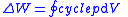 |
Statistical physics
Below are useful results from the Maxwell-Boltzmann distribution for an ideal gas, and the implications of the Entropy quantity. The distribution is valid for atoms or molecules constituting ideal gases.| Physical situation | Equations |
|---|---|
| Maxwell–Boltzmann distribution | Non-relativistic speeds Relativistic speeds (Maxwell-Juttner distribution) 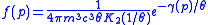 |
| v = velocity of atom/molecule, m = mass of each molecule (all molecules are identical in kinetic theory), γ(p) = Lorentz factor as function of momentum (see below) Ratio of thermal to rest mass-energy of each molecule:  K2 is the Modified Bessel function Bessel function In mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:... of the second kind. |
|
| Entropy Logarithm Logarithmic scale A logarithmic scale is a scale of measurement using the logarithm of a physical quantity instead of the quantity itself.A simple example is a chart whose vertical axis increments are labeled 1, 10, 100, 1000, instead of 1, 2, 3, 4... of the density of states Density of states In solid-state and condensed matter physics, the density of states of a system describes the number of states per interval of energy at each energy level that are available to be occupied by electrons. Unlike isolated systems, like atoms or molecules in gas phase, the density distributions are not... |
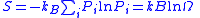 where:  |
| Pi = probability of system in microstate i Ω = total number of microstates |
|
| Entropy change | 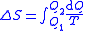  |
| Entropic force |  |
| Equipartition theorem | Average kinetic energy per degree of freedom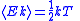 Internal energy 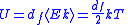 |
| df = degree of freedom | |
Corollaries of the non-relativistic Maxwell-Boltzmann distribution are below.
| Physical situation | Equations |
|---|---|
| Mean speed | 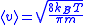 |
| Root mean square speed |  |
| Modal speed |  |
| Mean free path Mean free path In physics, the mean free path is the average distance covered by a moving particle between successive impacts which modify its direction or energy or other particle properties.-Derivation:... |
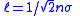 |
| σ = Effective cross-section n = Volume density of number of target particles l = Mean free path |
|
Thermal transfer
| Physical situation | Equations |
|---|---|
| Net intensity emission/absorption |  |
| Texternal = external temperature (outside of system) Tsystem = internal temperature (inside system) ε = emmisivity |
|
| Internal energy of a substance | 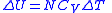 |
| CV = isovolumetric heat capacity of substance ΔT = temperature change of substance |
|
| Work done by an expanding ideal gas | 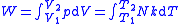 |
| Meyer's equation | 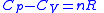 |
| Cp = isobaric heat capacity CV = isovolumetric heat capacity n = number of moles |
|
| Effective thermal conductivities | Series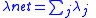 Parallel  |
| λi = thermal conductivity of substance i λnet = equivalent thermal conductivity |
|
Thermal efficiencies
| Physical situation | Equations |
|---|---|
| Thermodynamic engines | Thermodynamic engine: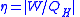 Carnot engine efficiency: 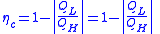 |
| η = efficiency W = work done by engine QH = heat energy in higher temperature resevior QC = heat energy in lower temperature resevior TH = temperature of higher temp. resevior TC = temperature of lower temp. resevior |
|
| Refrigeration | Refrigeration performance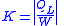 Carnot refrigeration performance  |
| K = coefficient of refrigeration performance |
|
Waves
In what follows n, m are any integers (Z = set of integers);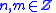 .
.Standing waves
| Physical situation | Equations |
|---|---|
| Harmonic frequencies | 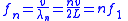 |
| fn = nth mode of vibration, nth harmonic, (n-1)th overtone | |
Propagating waves
Sound waves| Physical situation | Equations |
|---|---|
| Average wave power |  |
| P0 = Sound power due to source | |
| Sound intensity | 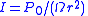  |
| Ω = Solid angle | |
| Acoustic beat frequency | |
| Doppler effect for mechanical waves | 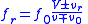 upper signs indicate relative approach, lower signs indicate relative recession. |
| V = speed of sound wave in medium f0 = Source frequency fr = Receiver frequency v0 = Source velocity vr = Receiver velocity |
|
| Mach cone angle (Supersonic shockwave, sonic boom) |  |
| v = speed of body v = local speed of sound θ = angle between direction of travel and conic evelope of superimposed wavefronts |
|
| Acoustic pressure and displacement amplitudes | 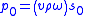 |
| p0 = pressure amplitude s0 = displacement amplitude v = speed of sound ρ = local density of medium |
|
| Wave functions for sound | Acoustic beats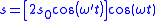 Sound displacement function  Sound pressure-variation 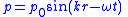 |
Gravitational waves
Gravitational radiation for two orbiting bodies in the low-speed limit.
| Physical situation | Equations |
|---|---|
| Radiated power | 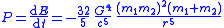 |
| P = Radiated power from system, t = time, r = separation between centres-of-mass m1, m2 = masses of the orbiting bodies |
|
| Orbital radius decay | 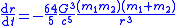 |
| Orbital lifetime |  |
| r0 = initial distance between the orbiting bodies | |
Superposition, interference, and diffraction
| Physical situation | Equations |
|---|---|
| Principle of superposition |  |
| N = number of waves | |
| Resonance |  |
| ωd = driving angular frequency (external agent) ωnat = natural angular frequency (oscillator) |
|
| Phase and interference | 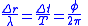 Constructive interference 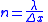 Destructive interference  |
| Δr = path length difference φ = phase difference between any two successive wave cycles |
|
Wave propagation
A common misconception occurs between phase velocity and group velocity (analogous to centres of mass and gravity). They happen to be equal in non-dispersive media. In dispersive media the phase velocity is not necessarily the same as the group velocity. The phase velocity varies with frequency.- The
Intuitively the wave envelope is the "global profile" of the wave, which "contains" changing "local profiles inside the global profile". Each propagates at generally different speeds determined by the important function called the Dispersion Relation
Dispersion relation
In physics and electrical engineering, dispersion most often refers to frequency-dependent effects in wave propagation. Note, however, that there are several other uses of the word "dispersion" in the physical sciences....
. The use of the explicit form ω(k) is standard, since the phase velocity ω/k and the group velocity dω/dk usually have convenient representations by this function.
| Physical situation | Equations |
|---|---|
| Idealized non-dispersive media | 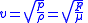 |
| p = (any type of) Stress or Pressure, ρ = Volume Mass Density, F = Tension Force, μ = Linear Mass Density of medium |
|
| Dispersion relation Dispersion relation In physics and electrical engineering, dispersion most often refers to frequency-dependent effects in wave propagation. Note, however, that there are several other uses of the word "dispersion" in the physical sciences.... |
Implicit form 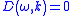 Explicit form  |
| Amplitude modulation Amplitude modulation Amplitude modulation is a technique used in electronic communication, most commonly for transmitting information via a radio carrier wave. AM works by varying the strength of the transmitted signal in relation to the information being sent... , AM |
 |
| Frequency modulation Frequency modulation In telecommunications and signal processing, frequency modulation conveys information over a carrier wave by varying its instantaneous frequency. This contrasts with amplitude modulation, in which the amplitude of the carrier is varied while its frequency remains constant... , FM |
 |
Wave equations
| Name | Wave equation | General solution/s |
|---|---|---|
| Non-dispersive Wave Equation Wave equation The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics... in 3d |
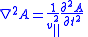 |
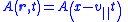 |
| A = amplitude as function of position and time | ||
| Exponentially damped waveform | 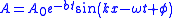 |
|
| A0 = Initial amplitude at time t = 0 b = damping parameter |
||
| Korteweg–de Vries equation Korteweg–de Vries equation In mathematics, the Korteweg–de Vries equation is a mathematical model of waves on shallow water surfaces. It is particularly notable as the prototypical example of an exactly solvable model, that is, a non-linear partial differential equation whose solutions can be exactly and precisely specified... |
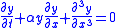 |
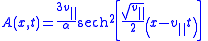 |
| α = constant | ||
Sinusoidal solutions to the 3d wave equation
N different sinusoidal wavesUsing complex numbers and applying the superposition to N waves of different amplitudes, frequencies, wavenumbers and phases, the general sinusoidal solution can be obtained.
The complex amplitudes are as follows.
Complex amplitude of wave n
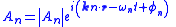
Resultant complex amplitude of all N waves
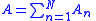
Modulus of amplitude

The transverse displacements are simply the real parts of the complex amplitudes.
Transverse displacement of wave n is
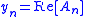
Resultant transverse displacement
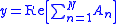
1 dimensional corollaries for two sinusoidal waves
The following may be deduced by applying the principle of superposition to two sinusoidal waves, using trigonometric identities. The angle addition and sum-to-product trigonometric formulae are useful; in more advanced work complex numbers and fourier series and transforms are used.
| Wavefunction | Superposition | Resultant |
|---|---|---|
| Standing wave | 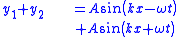 |
 |
| Beats | 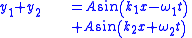 |
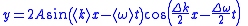 |
 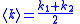  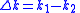 |
||
| Coherent interference | 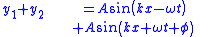 |
 |
Gravitational fields
General classical equations, also occur in relativity for weak-field limits. It can be shown that a uniform spherically symmetric mass distribution generates an equivalent gravitational field, so all formulae for point masses apply to bodies which can be modelled in this way.| Physical situation | Equations |
|---|---|
| Gravitational potential gradient and field |   |
| U = gravitational potential C = curved path traversed by a mass in the field |
|
| Point mass | |
| At a point in a local array of point masses | |
| Gravitational torque and potential energy due to non-uniform fields and mass moments | 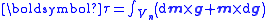 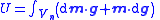 |
| V = volume of space occupied by the charge distribution | |
| Gravitational field for a rotating body |  |
φ = zenith angle relative to rotation axis  = unit vector perpendicular to rotation (zenith) axis, radial from it = unit vector perpendicular to rotation (zenith) axis, radial from it |
|
Weak-gravitational field relativistic equations:
| Physical situation | Equations |
|---|---|
| Gravitomagnetic field for a rotating body | |
Gravitational potentials
General classical equations.| Physical situation | Equations |
|---|
| Potential energy from gravity, integral from Newton's law |
|-
|style="background: #f2f2f2"| Escape speed
|rowspan="2"|
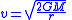
|-
| M = Mass of body (eg planet) to escape from
r = radius of body
|-
|style="background: #f2f2f2"| Orbital energy
|rowspan="2"|
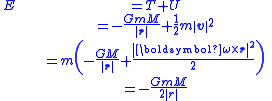
|-
| m = mass of orbiting body (eg planet)
M = mass of central body (eg star)
ω = angular velocity of orbiting mass
r = separation between centres of mass
T = kinetic energy
U = gravitational potential energy (sometimes called "gravitational binding energy" for this instance)
|-
|}
Electric fields
General Classical Equations| Physical situation | Equations |
|---|---|
| Electric potential gradient and field |   |
| Point Charge | |
| At a point in a local array of Point Charges | |
| At a Point due to a Continuum of Charge | |
| Electrostatic torque and potential energy due to non-uniform fields and dipole moments | 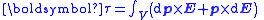 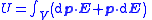 |
Magnetic fields and moments
General Classical Equations| Physical situation | Equations |
|---|---|
| Magnetic potential, EM vector potential | 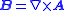 |
| Due to a magnetic moment | 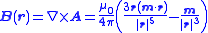 |
| Magnetic moment due to a current distribution |  |
| Magnetostatic torque and potential energy due to non-uniform fields and dipole moments | 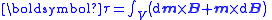 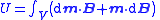 |
Electromagnetic induction
| Physical situation | Nomenclature | Equations |
|---|---|---|
| Transformation of voltage | N = number of turns of conductor η = energy efficiency |
 |
Electric circuits and electronics
Below N = number of conductors or circuit components. Subcript net refers to the equivalent and resultant property value.| Physical situation | Series | Parallel |
|---|---|---|
| Resistors and conductors | 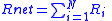  |
  |
| Ri = resistance of resistor or conductor i Gi = conductance of conductor or conductor i |
||
| Charge, capacitors, currents |    |
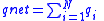 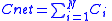 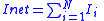 |
| qi = capacitance of capacitor i qi = charge of charge carrier i |
||
| Inductors |  |
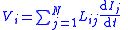 |
| Li = self inductance of inductor i Lij = self inductance element ij of L matrix Mij = mutual inductance between inductors i and j |
||
Series circuit equations
| Circuit | DC Circuit equations | AC Circuit equations |
|---|---|---|
| RC circuits | Circuit equation Capacitor charge 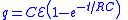 Capacitor discharge  |
|
| RL circuits | Circuit equation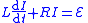 Inductor current rise 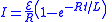 Inductor current fall 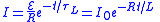 |
|
| LC circuits | Circuit equation |
Circuit equation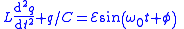 Circuit resonant frequency  Circuit charge 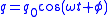 Circuit current 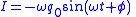 Circuit electrical potential energy  Circuit magnetic potential energy  |
| RLC Circuits | Circuit equation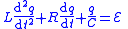 |
Circuit equation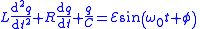 Circuit charge  |
Luminal electromagnetic waves
| Physical situation | Nomenclature | Equations |
|---|---|---|
| Energy density in an EM wave | 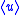 = mean energy density = mean energy density |
For a dielectric: |
| Kinetic and potential momenta Kinetic momentum In physics, in particular electromagnetism, the kinetic momentum is a nonstandard term for the momentum of a charged particle due to its inertia. When a charged particle interacts with an electromagnetic field , there are two momenta: due to its inertia and due to the field... (non-standard terms in use) |
Potential momentum: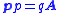 Kinetic momentum: 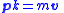 Cononical momentum: 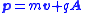 |
|
| Irradiance Irradiance Irradiance is the power of electromagnetic radiation per unit area incident on a surface. Radiant emittance or radiant exitance is the power per unit area radiated by a surface. The SI units for all of these quantities are watts per square meter , while the cgs units are ergs per square centimeter... , light intensity Light intensity Several measures of light are commonly known as intensity. These are obtained by dividing either a power or a luminous flux by a solid angle, a planar area, or a combination of the two... |
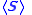 = time averaged poynting vector = time averaged poynting vectorI = irradiance Irradiance Irradiance is the power of electromagnetic radiation per unit area incident on a surface. Radiant emittance or radiant exitance is the power per unit area radiated by a surface. The SI units for all of these quantities are watts per square meter , while the cgs units are ergs per square centimeter... I0 = intensity of source P0 = power of point source Ω = solid angle r = radial position from source |
At a spherical surface:  |
| Doppler effect for light (relativistic) |  |
|
| Doppler Shift | ||
| Cherenkov radiation Cherenkov radiation Cherenkov radiation is electromagnetic radiation emitted when a charged particle passes through a dielectric medium at a speed greater than the phase velocity of light in that medium... , cone angle |
n = refractive index v = speed of particle θ = cone angle |
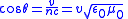 |
| Electric and magnetic amplitudes | E = electric field H = magnetic field strength |
|
| EM wave components | Electric 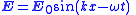 Magnetic  |
|
Geometric optics
| Physical situation | Equations |
|---|---|
| Critical angle Critical angle Critical angle can refer to:*Critical angle the angle of incidence above which total internal reflection occurs*Critical angle of attack, in aerodynamics; the angle of attack which produces the maximum lift coefficient... |
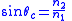 |
| n1 = refractive index of initial medium n2 = refractive index of final medium θc = critical angle |
|
| Thin lens Thin lens [Image:Lens1.svg|thumb|A lens can be considered a thin lens if d [Image:Lens1.svg|thumb|A lens can be considered a thin lens if d [Image:Lens1.svg|thumb|A lens can be considered a thin lens if d... equation |
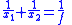 Lens Lens (optics) A lens is an optical device with perfect or approximate axial symmetry which transmits and refracts light, converging or diverging the beam. A simple lens consists of a single optical element... focal length Focal length The focal length of an optical system is a measure of how strongly the system converges or diverges light. For an optical system in air, it is the distance over which initially collimated rays are brought to a focus... from refraction Refraction Refraction is the change in direction of a wave due to a change in its speed. It is essentially a surface phenomenon . The phenomenon is mainly in governance to the law of conservation of energy. The proper explanation would be that due to change of medium, the phase velocity of the wave is changed... indices 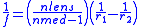 |
| f = lens focal length x1 = object length x2 = image length r1 = incident curvature radius r2 = refracted curvature radius |
|
| Image Image An image is an artifact, for example a two-dimensional picture, that has a similar appearance to some subject—usually a physical object or a person.-Characteristics:... distance in a plane mirror Plane mirror A plane mirror is a mirror with a plane reflective surface.For light rays striking a plane mirror, the angle of reflection equals the angle of incidence... |
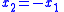 |
| Spherical mirror | Spherical mirror equation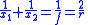 Image Image An image is an artifact, for example a two-dimensional picture, that has a similar appearance to some subject—usually a physical object or a person.-Characteristics:... distance in a spherical mirror 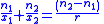 |
| r = curvature radius of mirror | |
Diffraction and interference
| Property or effect | Equation |
|---|---|
| Thin film Thin-film optics Thin-film optics is the branch of optics that deals with very thin structured layers of different materials. In order to exhibit thin-film optics, the thickness of the layers of material must be on the order of the wavelengths of visible light... in air |
Minima 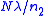 Maxima  |
| n1 = refractive index of initial medium (before film interference) n2 = refractive index of final medium (after film interference) |
|
| The grating equation |  |
| a = width of aperture, slit width α = incident angle to the normal of the grating plane |
|
| Single slit diffraction intensity | 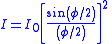 |
| I0 = source intensity Wave phase through apertures  |
|
| N-slit diffraction (N ≥ 2) | 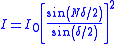 |
| d = centre-to-centre separation of slits N = number of slits Phase between N waves emerging from each slit 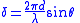 |
|
| N-slit diffraction (all N) | 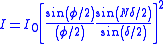 |
| Circular aperture intensity |  |
| a = radius of the circular aperture J1 is a Bessel function Bessel function In mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:... |
|
| Amplitude for a general planar aperture Cartesian and spherical polar coordinates are used, xy plane contains aperture |
Far-field (Fraunhofer)
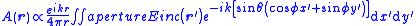
|-
| A, amplitude at position r
r' = source point in the aperture
Einc, magnitude of incident electric field at aperture
|-
|style="background: #f2f2f2"|Rayleigh's criterion
|
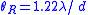
|-
|}
| Half-width | 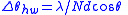 |
| Dispersion | 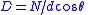 |
| Resolving power |  |
| Bragg's law Bragg's law In physics, Bragg's law gives the angles for coherent and incoherent scattering from a crystal lattice. When X-rays are incident on an atom, they make the electronic cloud move as does any electromagnetic wave... , Lattice distance |
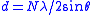 |
The Postulates of Quantum Mechanics
| Postulate 1: State of a system | A system is completely specified at any one time by a Hilbert space Hilbert space The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions... vector. |
| Postulate 2: Observables of a system | A measurable Observable In physics, particularly in quantum physics, a system observable is a property of the system state that can be determined by some sequence of physical operations. For example, these operations might involve submitting the system to various electromagnetic fields and eventually reading a value off... quantity corresponds to an operator Operational definition An operational definition defines something in terms of the specific process or set of validation tests used to determine its presence and quantity. That is, one defines something in terms of the operations that count as measuring it. The term was coined by Percy Williams Bridgman and is a part of... with eigenvectors spanning Linear span In the mathematical subfield of linear algebra, the linear span of a set of vectors in a vector space is the intersection of all subspaces containing that set... the space Vector space A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex... . |
| Postulate 3: Observation of a system | Measuring a system applies the observable's operator to the system and the system collapses into the observed eigenvector. |
| Postulate 4: Probabilistic result of measurement | The probability Probability Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The... of observing an eigenvector is derived from the square of its wavefunction Wavefunction Not to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of... . |
| Postulate 5: Time evolution of a system | The way the wavefunction evolves over time is determined by Shrodinger's equation. |
Other Equations
Wavefunction Characteristics| Property/Effect | Nomenclature | Equation |
|---|---|---|
| Normalization |  |
|
Probability Distributions
| Property/Effect | Nomenclature | Equation |
|---|---|---|
| Density of states Density of states In solid-state and condensed matter physics, the density of states of a system describes the number of states per interval of energy at each energy level that are available to be occupied by electrons. Unlike isolated systems, like atoms or molecules in gas phase, the density distributions are not... |
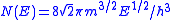 |
|
| Occupancy probability | 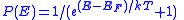 |
|
Angular momentum
| Property/effect | Nomenclature | Equation |
|---|---|---|
| Spin projection quantum number Quantum number Quantum numbers describe values of conserved quantities in the dynamics of the quantum system. Perhaps the most peculiar aspect of quantum mechanics is the quantization of observable quantities. This is distinguished from classical mechanics where the values can range continuously... |
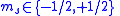 |
|
| Angular momentum Angular momentum In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system... components |
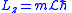 |
|
| Spin angular momentum magnitude |  |
|
Magnetic moments
| Property/Effect | Nomenclature | Equation |
|---|---|---|
| orbital magnetic dipole moment |  |
|
| orbital magnetic dipole moment components |  |
|
| spin magnetic dipole moment | 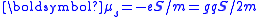 |
|
| orbital magnetic dipole moment |  |
|
| spin magnetic dipole moment potential |  |
|
| orbital magnetic dipole moment potential |  |
|
| Bohr magneton |  |
|
The Hydrogen atom
Hydrogen atom
A hydrogen atom is an atom of the chemical element hydrogen. The electrically neutral atom contains a single positively-charged proton and a single negatively-charged electron bound to the nucleus by the Coulomb force...
| Property/Effect | Nomenclature | Equation |
|---|---|---|
| Orbital energy | 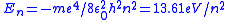 , for positive int n , for positive int n |
|
| Spectrum |  |
|
| Radial probability density |  |
|
Light
| Property/Effect | Nomenclature | Equation |
|---|---|---|
| Photoelectric equation |  |
|
| photon Photon In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force... momentum |
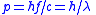 |
|
| Cutoff wavelength | 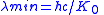 |
|
Common Cases
| Property/Effect | Nomenclature | Equation |
|---|---|---|
| Infinite potential well | 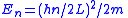 |
|
| wavefunction Wavefunction Not to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of... of a trapped electron Electromagnetic cavity An electromagnetic cavity is a cavity that acts as a container for electromagnetic fields such as photons, in effect containing their wave function inside. The size of the cavity determines the maximum photon wave length that can be trapped. Additionally, it produces quantized energy levels for... |
 , for positive int n , for positive int n |
|
Special relativity
Subscripts 0 refer to the frame F0, the frame observing frame F travel at speed v relative to F0. In frame F0 all subscript 0 quantities are proper lengths or times, or rest masses.Corollaries
| Physical situation | Equations |
|---|---|
| Lorentz factor Lorentz factor The Lorentz factor or Lorentz term appears in several equations in special relativity, including time dilation, length contraction, and the relativistic mass formula. Because of its ubiquity, physicists generally represent it with the shorthand symbol γ . It gets its name from its earlier... |
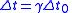 |
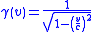 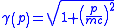 |
|
| Time dilation Time dilation In the theory of relativity, time dilation is an observed difference of elapsed time between two events as measured by observers either moving relative to each other or differently situated from gravitational masses. An accurate clock at rest with respect to one observer may be measured to tick at... |
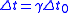 |
| t0 = elapsed time measured in inertial frame F0 = proper time for frame F0 t = elapsed time measured in inertial frame F moving at speed v relative to frame F0 |
|
| Length contraction Length contraction In physics, length contraction – according to Hendrik Lorentz – is the physical phenomenon of a decrease in length detected by an observer of objects that travel at any non-zero velocity relative to that observer... |
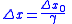 |
| x0 = measured distance in inertial frame F0 = proper length for frame F0 x = measured length in inertial frame F moving at speed v relative to frame F0 |
|
| Relativistic mass |
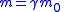 |
| m0 = measured mass in inertial frame F0 = rest mass for frame F0 m = measured mass in inertial frame F moving at speed v relative to frame F0 |
|
| 3-Momentum |  |
| Mass-energy equivalence Mass-energy equivalence In physics, mass–energy equivalence is the concept that the mass of a body is a measure of its energy content. In this concept, mass is a property of all energy, and energy is a property of all mass, and the two properties are connected by a constant... |
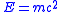 Rest mass-energy 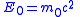 |
| Momentum-energy for massless particles |
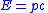 |
| Kinetic energy |
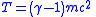 |
Particle physics
| Physical situation | Equations |
|---|---|
| Mass number Mass number The mass number , also called atomic mass number or nucleon number, is the total number of protons and neutrons in an atomic nucleus. Because protons and neutrons both are baryons, the mass number A is identical with the baryon number B as of the nucleus as of the whole atom or ion... |
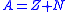 |
| A = (Relative) atomic mass = Mass number = Number of protons and neutrons N = Number of neutrons Z = Atomic number = Number of protons = Number of electrons |
|
| Mass in nuclei |
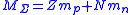    |
| Mnuc = Mass of nucleus, bound nucleons MΣ = Sum of masses for isolated nucleons mp = proton rest mass mn = neutron rest mass |
|
| Nuclear radius |
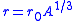 |
| r0 ≈ 1.2 fm | |
| Radioactive decay Radioactive decay Radioactive decay is the process by which an atomic nucleus of an unstable atom loses energy by emitting ionizing particles . The emission is spontaneous, in that the atom decays without any physical interaction with another particle from outside the atom... |
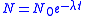 |
| N0 = Initial number of atoms N = Number of atoms at time t λ = Decay constant t = Time |
|
| Radiation flux Radiation flux Radiation flux is a measure of the flow of radiation from a given radioactive source.Radiation flux density is a related measure that adds area dimensions to the above definition - for example, radiation-flux/square-centimeter.... |
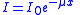 |
| I0 = Initial intensity/Flux of radiation I = Number of atoms at time t μ = Linear absorption coefficient x = Thickness of substance |
|
| Fermi energy Fermi energy The Fermi energy is a concept in quantum mechanics usually referring to the energy of the highest occupied quantum state in a system of fermions at absolute zero temperature.... |
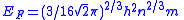 |
| Hubble's law Hubble's law Hubble's law is the name for the astronomical observation in physical cosmology that: all objects observed in deep space are found to have a doppler shift observable relative velocity to Earth, and to each other; and that this doppler-shift-measured velocity, of various galaxies receding from... |
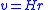 |
See also
Variables commonly used in physicsContinuity equation
Continuity equation
A continuity equation in physics is a differential equation that describes the transport of a conserved quantity. Since mass, energy, momentum, electric charge and other natural quantities are conserved under their respective appropriate conditions, a variety of physical phenomena may be described...
Constitutive equation
Constitutive equation
In physics, a constitutive equation is a relation between two physical quantities that is specific to a material or substance, and approximates the response of that material to external forces...
Operator (physics)
Operator (physics)
In physics, an operator is a function acting on the space of physical states. As a resultof its application on a physical state, another physical state is obtained, very often along withsome extra relevant information....
Defining equation (physical chemistry)
Defining equation (physical chemistry)
In physical chemistry, there are numerous quantities associated with chemical compounds and reactions; notably in terms of amounts of substance, activity or concentration of a substance, and the rate of reaction. This article uses SI units....
Physical constant
Physical constant
A physical constant is a physical quantity that is generally believed to be both universal in nature and constant in time. It can be contrasted with a mathematical constant, which is a fixed numerical value but does not directly involve any physical measurement.There are many physical constants in...
Sources
- Dynamics and Relativity, J.R. Forshaw, A.G. Smith, Wiley, 2009, ISBN 978 0 470 01460 8
- The Physics of Vibrations and Waves (3rd edition), H.J. Pain, John Wiley & Sons, 1983, ISBN 0 471 90182 2
- Essential Principles of Physics, P.M. Whelan, M.J. Hodgeson, 2nd Edition, 1978, John Murray, ISBN 0 7195 3382 1
- Electromagnetism (2nd edition), I.S. Grant, W.R. Phillips, Manchester Physics Series, 2008 ISBN 0 471 92712 0
- Encyclopaedia of Physics, R.G. Lerner, G.L. Trigg, 2nd Edition, VHC Publishers, Hans Warlimont, Springer, 2005, pp 12–13
- Physics for Scientists and Engineers: With Modern Physics (6th Edition), P.A. Tipler, G. Mosca, W.H. Freeman and Co, 2008, 9-781429-202657
- 3000 Solved Problems in Physics, Schaum Series, A. Halpern, Mc Graw Hill, 1988, ISBN 978-0-07-025734-4
External links
- Physics formulae at xs4all.nl
- Alternative version on wikiversity Tables of Physics Formulae Wikiversity
- http://mathworld.wolfram.com/SphericalCoordinates.html