
Thin lens
Encyclopedia
Optics
Optics is the branch of physics which involves the behavior and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behavior of visible, ultraviolet, and infrared light...
, a thin lens is a lens
Lens (optics)
A lens is an optical device with perfect or approximate axial symmetry which transmits and refracts light, converging or diverging the beam. A simple lens consists of a single optical element...
with a thickness (distance along the optical axis
Optical axis
An optical axis is a line along which there is some degree of rotational symmetry in an optical system such as a camera lens or microscope.The optical axis is an imaginary line that defines the path along which light propagates through the system...
between the two surfaces of the lens) that is negligible
Negligible
Negligible refers to the quantities so small that they can be ignored when studying the larger effect. Although related to the more mathematical concepts of infinitesimal, the idea of negligibility is particularly useful in practical disciplines like physics, chemistry, mechanical and electronic...
compared to the focal length
Focal length
The focal length of an optical system is a measure of how strongly the system converges or diverges light. For an optical system in air, it is the distance over which initially collimated rays are brought to a focus...
of the lens. Lenses whose thickness is not negligible are sometimes called thick lenses.
The thin lens approximation ignores optical effects due to the thickness of lenses and simplifies ray tracing
Ray tracing (physics)
In physics, ray tracing is a method for calculating the path of waves or particles through a system with regions of varying propagation velocity, absorption characteristics, and reflecting surfaces. Under these circumstances, wavefronts may bend, change direction, or reflect off surfaces,...
calculations. It is often combined with the paraxial approximation
Paraxial approximation
In geometric optics, the paraxial approximation is a small-angle approximation used in Gaussian optics and ray tracing of light through an optical system ....
in techniques such as ray transfer matrix analysis
Ray transfer matrix analysis
Ray transfer matrix analysis is a type of ray tracing technique used in the design of some optical systems, particularly lasers...
.
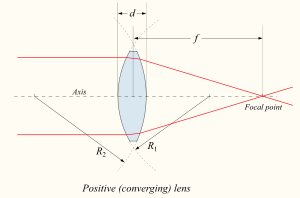
The focal length, f, of a thin lens is given by the Lensmaker's equation:

where n is the index of refraction of the lens material, and R1 and R2 are the radii of curvature of the two surfaces. Here, R1 is taken to be positive if the first surface is convex, and negative if the surface is concave. The signs are reversed for the back surface of the lens: R2 is positive if the surface is concave, and negative if it is convex. This is an arbitrary sign convention
Sign convention
In physics, a sign convention is a choice of the physical significance of signs for a set of quantities, in a case where the choice of sign is arbitrary. "Arbitrary" here means that the same physical system can be correctly described using different choices for the signs, as long as one set of...
; some authors choose different signs for the radii, which changes the equation for the focal length.
For a thin lens, in the paraxial ray approximation, the object (
 ) and image (
) and image (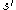 ) distances are related by the equation
) distances are related by the equation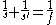 .
.In scalar wave optics a lens is a part which shifts the phase of the wave-front. Mathematically this can be understood as a multiplication of the wave-front with the following function:
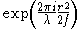 .
.

