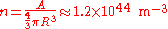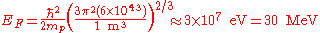
Fermi energy
Encyclopedia
The Fermi energy is a concept in quantum mechanics
usually referring to the energy of the highest occupied quantum state in a system of fermion
s at absolute zero
temperature
.
Confusingly, the term "Fermi energy" is often used to describe a different but closely related concept, the Fermi level
(also called chemical potential
). The Fermi energy and chemical potential are the same at absolute zero, but differ at other temperatures, as described below.
, a group of particles known as fermion
s (for example, electron
s, proton
s and neutron
s) obey the Pauli exclusion principle
. This states that no two fermions can occupy the same (one-particle) quantum state. The states are labeled by a set of quantum numbers. In a system containing many fermions (like electrons in a metal), each fermion will have a different set of quantum numbers. To determine the lowest energy a system of fermions can have, we first group the states into sets with equal energy, and order these sets by increasing energy. Starting with an empty system, we then add particles one at a time, consecutively filling up the unoccupied quantum states with the lowest energy. When all the particles have been put in, the Fermi energy is the energy of the highest occupied state.
What this means is that even if we have extracted all possible energy from a metal
by cooling it to near absolute zero temperature (0 kelvin
), the electrons in the metal are still moving around. The fastest ones are moving at a velocity corresponding to a kinetic energy equal to the Fermi energy. This is the Fermi velocity. The Fermi energy is one of the important concepts of condensed matter physics
. It is used, for example, to describe metals, insulators, and semiconductor
s. It is a very important quantity in the physics of superconductors, in the physics of quantum liquid
s like low temperature helium
(both normal and superfluid 3He), and it is quite important to nuclear physics
and to understand the stability of white dwarf stars
against gravitational collapse
.
s is the increase in the ground state
energy
when exactly one particle is added to the system. It can also be interpreted as the maximum energy of an individual fermion in this ground state. The chemical potential
at zero temperature is equal to the Fermi energy.
of length L is a model for a one dimensional box. It is a standard model-system in quantum mechanics for which the solution for a single particle is well known. The levels are labeled by a single quantum number n and the energies are given by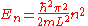
.
Suppose now that instead of one particle in this box we have N particles in the box and that these particles are fermions with spin 1/2. Then only two particles can have the same energy, i.e., two particles can have the energy of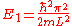
, or two particles can have energy 
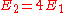and so forth. The reason that two particles can have the same energy is that a particle can have a spin of 1/2 (spin up) or a spin of -1/2 (spin down), leading to two states for each energy level. In the configuration for which the total energy is lowest (the ground state), all the energy levels up to n=N/2 are occupied and all the higher levels are empty. The Fermi energy is therefore
.
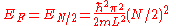Alternative Method for calculating Fermi-energy
Calculate the density of states using the ground state energy eigenstate for a free particle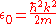
where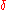
is the dirac delta function
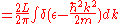
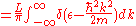
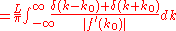
Note that we need two delta functions since there are two roots to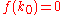
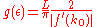
where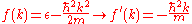
and 
.
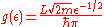
The integral of the density of states up to the Fermi-energy yields the number of particles
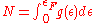
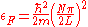
Let us now consider a three-dimensional cubical box that has a side length L (see infinite square well). This turns out to be a very good approximation for describing electrons in a metal.
The states are now labeled by three quantum numbers nx, ny, and nz. The single particle energies are
There are multiple states with the same energy, for example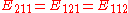
. Now let's put N non-interacting fermions of spin 1/2 into this box. To calculate the Fermi energy, we look at the case where N is large.
If we introduce a vector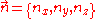
then each quantum state corresponds to a point in 'n-space' with energy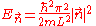
The number of states with energy less than Ef is equal to the number of states that lie within a sphere of radius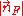
in the region of n-space where nx, ny, nz are positive. In the ground state this number equals the number of fermions in the system.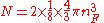
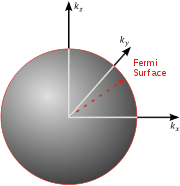the factor of two is once again because there are two spin states, the factor of 1/8 is because only 1/8 of the sphere lies in the region where all n are positive.
We find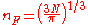
so the Fermi energy is given by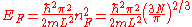
Which results in a relationship between the Fermi energy and the number of particles per volume (when we replace L2 with V2/3):
|
|}
The total energy of a Fermi sphere of
fermions is given by
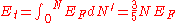
Therefore, the average energy of an electron is given by:
Alternative Method for calculating Fermi-energy
Calculate the density of states using the ground state energy eigenstate for a free particle
where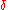
is the dirac delta function
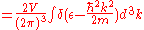
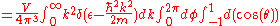
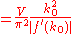
where
and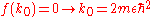 
.
The integral of the density of states up to the Fermi-energy yields the number of particles
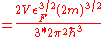
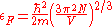
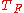, defined as 
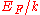, where 
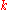is the Boltzmann constant. Other quantities defined in this context are Fermi momentum, 
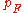, and Fermi velocity, 
, the momentum
and velocity
, respectively, of a fermion
at the Fermi surface
. (These quantities are not well-defined in cases where the Fermi surface is non-spherical). In the case of the Fermi sphere, they are given by: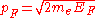
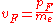
where
is the mass of the electron.
The Fermi momentum can also be described as
, where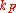 
is the radius of the Fermi sphere and is called the Fermi wave vector.
, but have about a hundredth of its radius. The high densities means that the electrons are no longer bound to single nuclei and instead form a degenerate
electron gas. The number density of electrons in a white dwarf are on the order of 1036 electrons/m3. This means their Fermi energy is:
The number density of nucleons in a nucleus is therefore:
Now since the Fermi energy only applies to fermions of the same type, one must divide this density in two. This is because the presence of neutron
s does not affect the Fermi energy of the proton
s in the nucleus, and vice versa.
So the Fermi energy of a nucleus is about:
The radius of the nucleus admits deviations around the value mentioned above, so a typical value for the Fermi energy usually given is 38 MeV
.
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
usually referring to the energy of the highest occupied quantum state in a system of fermion
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
s at absolute zero
Absolute zero
Absolute zero is the theoretical temperature at which entropy reaches its minimum value. The laws of thermodynamics state that absolute zero cannot be reached using only thermodynamic means....
temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
.
Confusingly, the term "Fermi energy" is often used to describe a different but closely related concept, the Fermi level
Fermi level
The Fermi level is a hypothetical level of potential energy for an electron inside a crystalline solid. Occupying such a level would give an electron a potential energy \epsilon equal to its chemical potential \mu as they both appear in the Fermi-Dirac distribution function,which...
(also called chemical potential
Chemical potential
Chemical potential, symbolized by μ, is a measure first described by the American engineer, chemist and mathematical physicist Josiah Willard Gibbs. It is the potential that a substance has to produce in order to alter a system...
). The Fermi energy and chemical potential are the same at absolute zero, but differ at other temperatures, as described below.
Context
In quantum mechanicsQuantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, a group of particles known as fermion
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
s (for example, electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
s, proton
Proton
The proton is a subatomic particle with the symbol or and a positive electric charge of 1 elementary charge. One or more protons are present in the nucleus of each atom, along with neutrons. The number of protons in each atom is its atomic number....
s and neutron
Neutron
The neutron is a subatomic hadron particle which has the symbol or , no net electric charge and a mass slightly larger than that of a proton. With the exception of hydrogen, nuclei of atoms consist of protons and neutrons, which are therefore collectively referred to as nucleons. The number of...
s) obey the Pauli exclusion principle
Pauli exclusion principle
The Pauli exclusion principle is the quantum mechanical principle that no two identical fermions may occupy the same quantum state simultaneously. A more rigorous statement is that the total wave function for two identical fermions is anti-symmetric with respect to exchange of the particles...
. This states that no two fermions can occupy the same (one-particle) quantum state. The states are labeled by a set of quantum numbers. In a system containing many fermions (like electrons in a metal), each fermion will have a different set of quantum numbers. To determine the lowest energy a system of fermions can have, we first group the states into sets with equal energy, and order these sets by increasing energy. Starting with an empty system, we then add particles one at a time, consecutively filling up the unoccupied quantum states with the lowest energy. When all the particles have been put in, the Fermi energy is the energy of the highest occupied state.
What this means is that even if we have extracted all possible energy from a metal
Metal
A metal , is an element, compound, or alloy that is a good conductor of both electricity and heat. Metals are usually malleable and shiny, that is they reflect most of incident light...
by cooling it to near absolute zero temperature (0 kelvin
Kelvin
The kelvin is a unit of measurement for temperature. It is one of the seven base units in the International System of Units and is assigned the unit symbol K. The Kelvin scale is an absolute, thermodynamic temperature scale using as its null point absolute zero, the temperature at which all...
), the electrons in the metal are still moving around. The fastest ones are moving at a velocity corresponding to a kinetic energy equal to the Fermi energy. This is the Fermi velocity. The Fermi energy is one of the important concepts of condensed matter physics
Condensed matter physics
Condensed matter physics deals with the physical properties of condensed phases of matter. These properties appear when a number of atoms at the supramolecular and macromolecular scale interact strongly and adhere to each other or are otherwise highly concentrated in a system. The most familiar...
. It is used, for example, to describe metals, insulators, and semiconductor
Semiconductor
A semiconductor is a material with electrical conductivity due to electron flow intermediate in magnitude between that of a conductor and an insulator. This means a conductivity roughly in the range of 103 to 10−8 siemens per centimeter...
s. It is a very important quantity in the physics of superconductors, in the physics of quantum liquid
Superfluid
Superfluidity is a state of matter in which the matter behaves like a fluid without viscosity and with extremely high thermal conductivity. The substance, which appears to be a normal liquid, will flow without friction past any surface, which allows it to continue to circulate over obstructions and...
s like low temperature helium
Helium
Helium is the chemical element with atomic number 2 and an atomic weight of 4.002602, which is represented by the symbol He. It is a colorless, odorless, tasteless, non-toxic, inert, monatomic gas that heads the noble gas group in the periodic table...
(both normal and superfluid 3He), and it is quite important to nuclear physics
Nuclear physics
Nuclear physics is the field of physics that studies the building blocks and interactions of atomic nuclei. The most commonly known applications of nuclear physics are nuclear power generation and nuclear weapons technology, but the research has provided application in many fields, including those...
and to understand the stability of white dwarf stars
White dwarf
A white dwarf, also called a degenerate dwarf, is a small star composed mostly of electron-degenerate matter. They are very dense; a white dwarf's mass is comparable to that of the Sun and its volume is comparable to that of the Earth. Its faint luminosity comes from the emission of stored...
against gravitational collapse
Gravitational collapse
Gravitational collapse is the inward fall of a body due to the influence of its own gravity. In any stable body, this gravitational force is counterbalanced by the internal pressure of the body, in the opposite direction to the force of gravity...
.
Advanced context
The Fermi energy (EF) of a system of non-interacting fermionFermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
s is the increase in the ground state
Ground state
The ground state of a quantum mechanical system is its lowest-energy state; the energy of the ground state is known as the zero-point energy of the system. An excited state is any state with energy greater than the ground state...
energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
when exactly one particle is added to the system. It can also be interpreted as the maximum energy of an individual fermion in this ground state. The chemical potential
Chemical potential
Chemical potential, symbolized by μ, is a measure first described by the American engineer, chemist and mathematical physicist Josiah Willard Gibbs. It is the potential that a substance has to produce in order to alter a system...
at zero temperature is equal to the Fermi energy.
Illustration of the concept for a one dimensional square well
The one dimensional infinite square wellParticle in a box
In quantum mechanics, the particle in a box model describes a particle free to move in a small space surrounded by impenetrable barriers. The model is mainly used as a hypothetical example to illustrate the differences between classical and quantum systems...
of length L is a model for a one dimensional box. It is a standard model-system in quantum mechanics for which the solution for a single particle is well known. The levels are labeled by a single quantum number n and the energies are given by
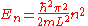.Suppose now that instead of one particle in this box we have N particles in the box and that these particles are fermions with spin 1/2. Then only two particles can have the same energy, i.e., two particles can have the energy of
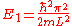, or two particles can have energy 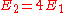and so forth. The reason that two particles can have the same energy is that a particle can have a spin of 1/2 (spin up) or a spin of -1/2 (spin down), leading to two states for each energy level. In the configuration for which the total energy is lowest (the ground state), all the energy levels up to n=N/2 are occupied and all the higher levels are empty. The Fermi energy is therefore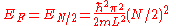.Alternative Method for calculating Fermi-energy
Calculate the density of states using the ground state energy eigenstate for a free particle
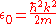
where
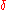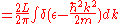
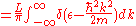
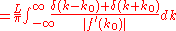
is the dirac delta functionNote that we need two delta functions since there are two roots to
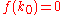
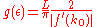
where
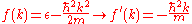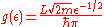
and .The integral of the density of states up to the Fermi-energy yields the number of particles
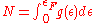
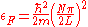
The three-dimensional case
The three-dimensional isotropic case is known as the Fermi sphere.Let us now consider a three-dimensional cubical box that has a side length L (see infinite square well). This turns out to be a very good approximation for describing electrons in a metal.
The states are now labeled by three quantum numbers nx, ny, and nz. The single particle energies are
-
- nx, ny, nz are positive integers.
There are multiple states with the same energy, for example
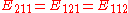. Now let's put N non-interacting fermions of spin 1/2 into this box. To calculate the Fermi energy, we look at the case where N is large.If we introduce a vector
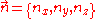then each quantum state corresponds to a point in 'n-space' with energy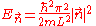The number of states with energy less than Ef is equal to the number of states that lie within a sphere of radius
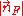in the region of n-space where nx, ny, nz are positive. In the ground state this number equals the number of fermions in the system.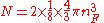We find
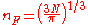
so the Fermi energy is given by
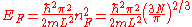
Which results in a relationship between the Fermi energy and the number of particles per volume (when we replace L2 with V2/3):
-
- {|cellpadding="2" style="border:2px solid #ccccff"
|
|}
The total energy of a Fermi sphere of
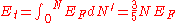
fermions is given byTherefore, the average energy of an electron is given by:
Alternative Method for calculating Fermi-energy
Calculate the density of states using the ground state energy eigenstate for a free particle
where
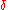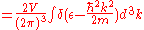
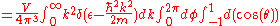
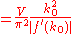
is the dirac delta functionwhere
and 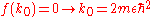.The integral of the density of states up to the Fermi-energy yields the number of particles
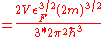
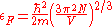
Related quantities
A related quantity is Fermi temperature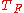, defined as 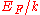, where 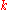is the Boltzmann constant. Other quantities defined in this context are Fermi momentum, 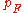, and Fermi velocity, , the momentumMomentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
and velocity
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
, respectively, of a fermion
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
at the Fermi surface
Fermi surface
In condensed matter physics, the Fermi surface is an abstract boundary useful for predicting the thermal, electrical, magnetic, and optical properties of metals, semimetals, and doped semiconductors. The shape of the Fermi surface is derived from the periodicity and symmetry of the crystalline...
. (These quantities are not well-defined in cases where the Fermi surface is non-spherical). In the case of the Fermi sphere, they are given by:
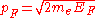
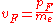
where
is the mass of the electron.The Fermi momentum can also be described as
, where 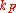is the radius of the Fermi sphere and is called the Fermi wave vector. White dwarfs
Stars known as white dwarfs have mass comparable to our SunSun
The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...
, but have about a hundredth of its radius. The high densities means that the electrons are no longer bound to single nuclei and instead form a degenerate
Degenerate matter
Degenerate matter is matter that has such extraordinarily high density that the dominant contribution to its pressure is attributable to the Pauli exclusion principle. The pressure maintained by a body of degenerate matter is called the degeneracy pressure, and arises because the Pauli principle...
electron gas. The number density of electrons in a white dwarf are on the order of 1036 electrons/m3. This means their Fermi energy is:
Nucleus
Another typical example is that of the particles in a nucleus of an atom. The radius of the nucleus is roughly:-
- where A is the number of nucleons.
The number density of nucleons in a nucleus is therefore:
Now since the Fermi energy only applies to fermions of the same type, one must divide this density in two. This is because the presence of neutron
Neutron
The neutron is a subatomic hadron particle which has the symbol or , no net electric charge and a mass slightly larger than that of a proton. With the exception of hydrogen, nuclei of atoms consist of protons and neutrons, which are therefore collectively referred to as nucleons. The number of...
s does not affect the Fermi energy of the proton
Proton
The proton is a subatomic particle with the symbol or and a positive electric charge of 1 elementary charge. One or more protons are present in the nucleus of each atom, along with neutrons. The number of protons in each atom is its atomic number....
s in the nucleus, and vice versa.
So the Fermi energy of a nucleus is about:
The radius of the nucleus admits deviations around the value mentioned above, so a typical value for the Fermi energy usually given is 38 MeV
MEV
MeV and meV are multiples and submultiples of the electron volt unit referring to 1,000,000 eV and 0.001 eV, respectively.Mev or MEV may refer to:In entertainment:* Musica Elettronica Viva, an Italian musical group...
.
See also
- Fermi-Dirac statisticsFermi-Dirac statisticsFermi–Dirac statistics is a part of the science of physics that describes the energies of single particles in a system comprising many identical particles that obey the Pauli Exclusion Principle...
- Fermi gasFermi gasA Fermi gas is an ensemble of a large number of fermions. Fermions, named after Enrico Fermi, are particles that obey Fermi–Dirac statistics. These statistics determine the energy distribution of fermions in a Fermi gas in thermal equilibrium, and is characterized by their number density,...
- Quasi Fermi levelQuasi Fermi levelA Quasi Fermi level is a term used in quantum mechanics and especially in solid state physics for the new Fermi level that describes the population of each type of charge carrier in a semiconductor separately when their populations are displaced from equilibrium...
- ThermodynamicsThermodynamicsThermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...
- SemiconductorSemiconductorA semiconductor is a material with electrical conductivity due to electron flow intermediate in magnitude between that of a conductor and an insulator. This means a conductivity roughly in the range of 103 to 10−8 siemens per centimeter...
s