
Nilpotent group
Encyclopedia
In mathematics
, more specifically in the field of group theory
, a nilpotent group is a group that is "almost abelian
". This idea is motivated by the fact that nilpotent groups are solvable
, and for finite nilpotent groups, two elements having relatively prime orders must commute. It is also true that finite nilpotent groups are supersolvable
.
Nilpotent groups arise in Galois theory
, as well as in the classification of groups. They also appear prominently in the classification of Lie group
s.
Analogous terms are used for Lie algebra
s (using the Lie bracket
) including nilpotent, lower central series, and upper central series.
for a group.
The following are equivalent formulations:
For a nilpotent group, the smallest n such that G has a central series of length n is called the nilpotency class of G ; and G is said to be nilpotent of class n. (By definition, the length is n if there are n + 1 different subgroups in the series, including the trivial subgroup and the whole group.)
Equivalently, the nilpotency class of G equals the length of the lower central series or upper central series.
If a group has nilpotency class at most m, then it is sometimes called a nil-m group.
It follows immediately from any of the above forms of the definition of nilpotency, that the trivial group is the unique group of nilpotency class 0, and groups of nilpotency class 1 are exactly the non-trivial abelian groups.
, meaning that for a nilpotent group G of nilpotence degree n and an element g, the function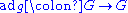 defined by
defined by 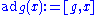 (where
(where 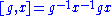 is the commutator
is the commutator
of g and x) is nilpotent in the sense that the nth iteration of the function is trivial: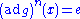 for all
for all  in
in  .
.
This is not a defining characteristic of nilpotent groups: groups for which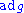 is nilpotent of degree n (in the sense above) are called n-Engel group
is nilpotent of degree n (in the sense above) are called n-Engel group
s, and need not be nilpotent in general. They are proven to be nilpotent if they have finite order
, and are conjectured to be nilpotent as long as they are finitely generated
.
An abelian group is precisely one for which the adjoint action is not just nilpotent but trivial (a 1-Engel group).
is abelian, and the series is finite, every nilpotent group is a solvable group
with a relatively simple structure.
Every subgroup of a nilpotent group of class n is nilpotent of class at most n; in addition, if f is a homomorphism
of a nilpotent group of class n, then the image of f is nilpotent of class at most n.
The following statements are equivalent for finite groups, revealing some useful properties of nilpotency:
The last statement can be extended to infinite groups: if G is a nilpotent group, then every Sylow subgroup Gp of G is normal, and the direct product of these Sylow subgroups is the subgroup of all elements of finite order in G (see torsion subgroup
).
Many properties of nilpotent groups are shared by hypercentral groups.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, more specifically in the field of group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, a nilpotent group is a group that is "almost abelian
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
". This idea is motivated by the fact that nilpotent groups are solvable
Solvable group
In mathematics, more specifically in the field of group theory, a solvable group is a group that can be constructed from abelian groups using extensions...
, and for finite nilpotent groups, two elements having relatively prime orders must commute. It is also true that finite nilpotent groups are supersolvable
Supersolvable group
In mathematics, a group is supersolvable if it has an invariant normal series where all the factors are cyclic groups. Supersolvability is stronger than the notion of solvability.-Definition:Let G be a group...
.
Nilpotent groups arise in Galois theory
Galois theory
In mathematics, more specifically in abstract algebra, Galois theory, named after Évariste Galois, provides a connection between field theory and group theory...
, as well as in the classification of groups. They also appear prominently in the classification of Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s.
Analogous terms are used for Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
s (using the Lie bracket
Lie bracket of vector fields
In the mathematical field of differential topology, the Lie bracket of vector fields, Jacobi–Lie bracket, or commutator of vector fields is a bilinear differential operator which assigns, to any two vector fields X and Y on a smooth manifold M, a third vector field denoted [X, Y]...
) including nilpotent, lower central series, and upper central series.
Definition
The definition uses the idea, explained on its own page, of a central seriesCentral series
In mathematics, especially in the fields of group theory and Lie theory, a central series is a kind of normal series of subgroups or Lie subalgebras, expressing the idea that the commutator is nearly trivial...
for a group.
The following are equivalent formulations:
- A nilpotent group is one that has a central seriesCentral seriesIn mathematics, especially in the fields of group theory and Lie theory, a central series is a kind of normal series of subgroups or Lie subalgebras, expressing the idea that the commutator is nearly trivial...
of finite length. - A nilpotent group is one whose lower central series terminates in the trivial subgroup after finitely many steps.
- A nilpotent group is one whose upper central series terminates in the whole group after finitely many steps.
For a nilpotent group, the smallest n such that G has a central series of length n is called the nilpotency class of G ; and G is said to be nilpotent of class n. (By definition, the length is n if there are n + 1 different subgroups in the series, including the trivial subgroup and the whole group.)
Equivalently, the nilpotency class of G equals the length of the lower central series or upper central series.
If a group has nilpotency class at most m, then it is sometimes called a nil-m group.
It follows immediately from any of the above forms of the definition of nilpotency, that the trivial group is the unique group of nilpotency class 0, and groups of nilpotency class 1 are exactly the non-trivial abelian groups.
Examples
- As noted above, every abelian group is nilpotent.
- For a small non-abelian example, consider the quaternion groupQuaternion groupIn group theory, the quaternion group is a non-abelian group of order eight, isomorphic to a certain eight-element subset of the quaternions under multiplication...
Q8, which is a smallest non-abelian p-group. It has center {1, −1} of order 2, and its upper central series is {1}, {1, −1}, Q8; so it is nilpotent of class 2. - All finite p-groupP-groupIn mathematics, given a prime number p, a p-group is a periodic group in which each element has a power of p as its order: each element is of prime power order. That is, for each element g of the group, there exists a nonnegative integer n such that g to the power pn is equal to the identity element...
s are in fact nilpotent (proof). The maximal class of a group of order pn is n - 1. The 2-groups of maximal class are the generalised quaternion groupQuaternion groupIn group theory, the quaternion group is a non-abelian group of order eight, isomorphic to a certain eight-element subset of the quaternions under multiplication...
s, the dihedral groupDihedral groupIn mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
s, and the semidihedral groups. - The direct productDirect productIn mathematics, one can often define a direct product of objectsalready known, giving a new one. This is generally the Cartesian product of the underlying sets, together with a suitably defined structure on the product set....
of two nilpotent groups is nilpotent. - Conversely, every finite nilpotent group is the direct product of p-groups.
- The Heisenberg group is an example of non-abelian, infinite nilpotent group.
- The multiplicative group of upper unitriangularUnipotentIn mathematics, a unipotent element r of a ring R is one such that r − 1 is a nilpotent element, in other words such that some power n is zero....
n x n matrices over any field F is a nilpotent group of nilpotent length n - 1 . - The multiplicative group of invertible upper triangularBorel subgroupIn the theory of algebraic groups, a Borel subgroup of an algebraic group G is a maximal Zariski closed and connected solvable algebraic subgroup.For example, in the group GLn ,...
n x n matrices over a field F is not in general nilpotent, but is solvableSolvable groupIn mathematics, more specifically in the field of group theory, a solvable group is a group that can be constructed from abelian groups using extensions...
.
Explanation of term
Nilpotent groups are so called because the "adjoint action" of any element is nilpotentNilpotent
In mathematics, an element x of a ring R is called nilpotent if there exists some positive integer n such that xn = 0....
, meaning that for a nilpotent group G of nilpotence degree n and an element g, the function
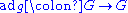 defined by
defined by 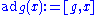 (where
(where 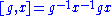 is the commutator
is the commutatorCommutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
of g and x) is nilpotent in the sense that the nth iteration of the function is trivial:
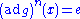 for all
for all  in
in  .
.This is not a defining characteristic of nilpotent groups: groups for which
 is nilpotent of degree n (in the sense above) are called n-Engel group
is nilpotent of degree n (in the sense above) are called n-Engel groupEngel group
In mathematics, an element x of a Lie group or a Lie algebra is called an n-Engel element, named after Friedrich Engel, if it satisfies the n-Engel condition that the repeated commutator...
s, and need not be nilpotent in general. They are proven to be nilpotent if they have finite order
Order (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
, and are conjectured to be nilpotent as long as they are finitely generated
Generating set of a group
In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
.
An abelian group is precisely one for which the adjoint action is not just nilpotent but trivial (a 1-Engel group).
Properties
Since each successive factor group Zi+1/Zi in the upper central seriesCentral series
In mathematics, especially in the fields of group theory and Lie theory, a central series is a kind of normal series of subgroups or Lie subalgebras, expressing the idea that the commutator is nearly trivial...
is abelian, and the series is finite, every nilpotent group is a solvable group
Solvable group
In mathematics, more specifically in the field of group theory, a solvable group is a group that can be constructed from abelian groups using extensions...
with a relatively simple structure.
Every subgroup of a nilpotent group of class n is nilpotent of class at most n; in addition, if f is a homomorphism
Group homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
of a nilpotent group of class n, then the image of f is nilpotent of class at most n.
The following statements are equivalent for finite groups, revealing some useful properties of nilpotency:
- G is a nilpotent group.
- If H is a proper subgroup of G, then H is a proper normal subgroupNormal subgroupIn abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
of NG(H) (the normalizer of H in G). This is called the normalizer property and can be phrased simply as "normalizers grow". - Every maximal proper subgroup of G is normal.
- G is the direct productDirect product of groupsIn the mathematical field of group theory, the direct product is an operation that takes two groups and and constructs a new group, usually denoted...
of its Sylow subgroups.
The last statement can be extended to infinite groups: if G is a nilpotent group, then every Sylow subgroup Gp of G is normal, and the direct product of these Sylow subgroups is the subgroup of all elements of finite order in G (see torsion subgroup
Torsion subgroup
In the theory of abelian groups, the torsion subgroup AT of an abelian group A is the subgroup of A consisting of all elements that have finite order...
).
Many properties of nilpotent groups are shared by hypercentral groups.

