L-moment
Encyclopedia
In statistics
, L-moments are statistics used to summarize the shape of a probability distribution
. They are analogous to conventional moments
in that they can be used to calculate quantities analogous to standard deviation
, skewness
and kurtosis
, termed the L-scale, L-skewness and L-kurtosis respectively (the L-mean is identical to the conventional mean
). Standardised L-moments are called L-moment ratios and these are
analogous to standardized moments.
L-moments differ from conventional moments in that they are calculated using linear combinations of the ordered data; the "l" in "linear" is what leads to the name being "L-moments". Just as for conventional moments, a theoretical distribution has a set of population L-moments. Estimates of the population L-moments (sample L-moments) can be defined for a sample from the population.
where Xk:n denotes the kth order statistic
(kth smallest value) in an independent
sample of size n from the distribution of X and
denotes expected value
. In particular, the first four population L-moments are
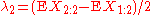
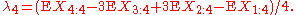
The first two of these L-moments have conventional names:
The L-scale is equal to half the mean difference
.
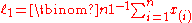
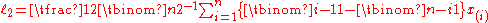
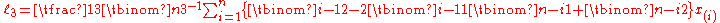
where is the th order statistic
and
is a binomial coefficient
. Sample L-moments can also be defined indirectly in terms of probability weighted moments, which leads to a more efficient algorithm
for their computation.
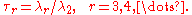
The most useful of these are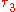
, called the L-skewness, and 
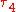, the L-kurtosis.
L-moment ratios lie within the interval (–1, 1). Tighter bounds can be found for some specific L-moment ratios; in particular, the L-kurtosis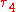
lies in [-¼,1), and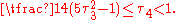
A quantity analogous to the coefficient of variation
, but based on L-moments, can also be defined:
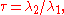
which is called the "coefficient of L-variation", or "L-CV". For a non-negative random variable, this lies in the interval (0,1) and is identical to the Gini coefficient
.
In statistics the latter is most commonly done using maximum likelihood
methods or using the method of moments
, however using L-moments provides an alternative method of parameter estimation. The former can also be performed using conventional moments, however using L-moments provides many advantages. As an example consider a dataset with a few data points and one outlying data value. If the ordinary standard deviation
of this data set is taken it will be highly influenced by this one point: however, if the L-scale is taken it will be far less sensitive to this data value. Consequently L-moments are far more meaningful when dealing with outliers in data than conventional moments. One example of this is using L-moments as summary statistics in extreme value theory
(EVT).
Another advantage L-moments have over conventional moments is that their existence only requires the random variable to have finite mean, so the L-moments exist even if the higher conventional moments do not exist (for example, for Student's t distribution with low degrees of freedom
). A finite variance is required in addition in order for the standard errors of estimates of the L-moments to be finite.
Some appearances of L-moments in the statistical literature include the book by David & Nagaraja (2003, Section 9.9) and a number of papers.
A number of favourable comparisons of L-moments with ordinary moments have been reported.
More complex expressions have been derived for some further distributions for which the L-moment ratios vary with one or more of the distributional parameters, including the log-normal, Gamma, generalized Pareto, generalized extreme value, and generalized logistic
distributions.
The notation for the parameters of each distribution is the same as that used in the linked article. In the expression for the mean of the Gumbel distribution, γ is the Euler–Mascheroni constant
0.57721… .
.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, L-moments are statistics used to summarize the shape of a probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
. They are analogous to conventional moments
Moment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
in that they can be used to calculate quantities analogous to standard deviation
Standard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
, skewness
Skewness
In probability theory and statistics, skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable. The skewness value can be positive or negative, or even undefined...
and kurtosis
Kurtosis
In probability theory and statistics, kurtosis is any measure of the "peakedness" of the probability distribution of a real-valued random variable...
, termed the L-scale, L-skewness and L-kurtosis respectively (the L-mean is identical to the conventional mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
). Standardised L-moments are called L-moment ratios and these are
analogous to standardized moments.
L-moments differ from conventional moments in that they are calculated using linear combinations of the ordered data; the "l" in "linear" is what leads to the name being "L-moments". Just as for conventional moments, a theoretical distribution has a set of population L-moments. Estimates of the population L-moments (sample L-moments) can be defined for a sample from the population.
Population L-moments
For a random variable X, the rth population L-moment iswhere Xk:n denotes the kth order statistic
Order statistic
In statistics, the kth order statistic of a statistical sample is equal to its kth-smallest value. Together with rank statistics, order statistics are among the most fundamental tools in non-parametric statistics and inference....
(kth smallest value) in an independent
Statistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
sample of size n from the distribution of X and
denotes expected valueExpected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
. In particular, the first four population L-moments are
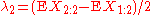
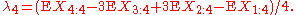
The first two of these L-moments have conventional names:
The L-scale is equal to half the mean difference
Mean difference
The mean difference is a measure of statistical dispersion equal to the average absolute difference of two independent values drawn from a probability distribution. A related statistic is the relative mean difference, which is the mean difference divided by the arithmetic mean...
.
Sample L-moments
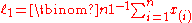
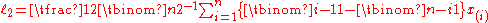
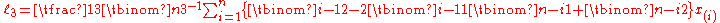
Direct estimators for the first four L-moments in a finite sample of n observations are:where is the th order statistic
Order statistic
In statistics, the kth order statistic of a statistical sample is equal to its kth-smallest value. Together with rank statistics, order statistics are among the most fundamental tools in non-parametric statistics and inference....
and
is a binomial coefficientBinomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
. Sample L-moments can also be defined indirectly in terms of probability weighted moments, which leads to a more efficient algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
for their computation.
L-moment ratios
A set of L-moment ratios, or scaled L-moments, is defined by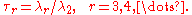The most useful of these are
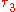, called the L-skewness, and 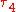, the L-kurtosis.L-moment ratios lie within the interval (–1, 1). Tighter bounds can be found for some specific L-moment ratios; in particular, the L-kurtosis
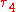lies in [-¼,1), and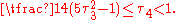A quantity analogous to the coefficient of variation
Coefficient of variation
In probability theory and statistics, the coefficient of variation is a normalized measure of dispersion of a probability distribution. It is also known as unitized risk or the variation coefficient. The absolute value of the CV is sometimes known as relative standard deviation , which is...
, but based on L-moments, can also be defined:
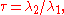
which is called the "coefficient of L-variation", or "L-CV". For a non-negative random variable, this lies in the interval (0,1) and is identical to the Gini coefficient
Gini coefficient
The Gini coefficient is a measure of statistical dispersion developed by the Italian statistician and sociologist Corrado Gini and published in his 1912 paper "Variability and Mutability" ....
.
Usage
There are two common ways that L-moments are used:- As summary statistics for data.
- To derive estimates for the parameters of probability distributions.
In statistics the latter is most commonly done using maximum likelihood
Maximum likelihood
In statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
methods or using the method of moments
Method of moments
Method of moments may refer to:* Method of moments , a method of parameter estimation in statistics* Method of moments , a way of proving convergence in distribution in probability theory...
, however using L-moments provides an alternative method of parameter estimation. The former can also be performed using conventional moments, however using L-moments provides many advantages. As an example consider a dataset with a few data points and one outlying data value. If the ordinary standard deviation
Standard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
of this data set is taken it will be highly influenced by this one point: however, if the L-scale is taken it will be far less sensitive to this data value. Consequently L-moments are far more meaningful when dealing with outliers in data than conventional moments. One example of this is using L-moments as summary statistics in extreme value theory
Extreme value theory
Extreme value theory is a branch of statistics dealing with the extreme deviations from the median of probability distributions. The general theory sets out to assess the type of probability distributions generated by processes...
(EVT).
Another advantage L-moments have over conventional moments is that their existence only requires the random variable to have finite mean, so the L-moments exist even if the higher conventional moments do not exist (for example, for Student's t distribution with low degrees of freedom
Degrees of freedom (statistics)
In statistics, the number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary.Estimates of statistical parameters can be based upon different amounts of information or data. The number of independent pieces of information that go into the...
). A finite variance is required in addition in order for the standard errors of estimates of the L-moments to be finite.
Some appearances of L-moments in the statistical literature include the book by David & Nagaraja (2003, Section 9.9) and a number of papers.
A number of favourable comparisons of L-moments with ordinary moments have been reported.
Values for some common distributions
The table below gives expressions for the first two L-moments and numerical values of the first two L-moment ratios of some common continuous probability distributions with constant L-moment ratios.More complex expressions have been derived for some further distributions for which the L-moment ratios vary with one or more of the distributional parameters, including the log-normal, Gamma, generalized Pareto, generalized extreme value, and generalized logistic
Generalized logistic distribution
The term generalized logistic distribution is used as the name for several different families of probability distributions. For example, Johnson et al. list four forms, which are listed below. One family described here has also been called the skew-logistic distribution...
distributions.
| Distribution | Parameters | mean, | L-scale, | L-skewness, | L-kurtosis, |
|---|---|---|---|---|---|
| Uniform | a, b | (a+b) / 2 | (b–a) / 6 | 0 | 0 |
| Logistic | μ, s | μ | s | 0 | |
| Normal | μ, σ2 | μ | σ / √π | 0 | 0.1226 |
| Laplace | μ, b | μ | 3b / 4 | 0 | |
| Student's t, 2 d.f. Degrees of freedom (statistics) In statistics, the number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary.Estimates of statistical parameters can be based upon different amounts of information or data. The number of independent pieces of information that go into the... |
ν = 2 | 0 | π/23/2 = 1.111 | 0 | |
| Student's t, 4 d.f. Degrees of freedom (statistics) In statistics, the number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary.Estimates of statistical parameters can be based upon different amounts of information or data. The number of independent pieces of information that go into the... |
ν = 4 | 0 | 15π/64 = 0.7363 | 0 | |
| Exponential Exponential distribution In probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e... |
λ | 1 / λ | 1 / (2λ) | ||
| Gumbel | μ, β | μ + γ Euler–Mascheroni constant The Euler–Mascheroni constant is a mathematical constant recurring in analysis and number theory, usually denoted by the lowercase Greek letter .... β |
β log 2 | 0.1699 | 0.1504 |
The notation for the parameters of each distribution is the same as that used in the linked article. In the expression for the mean of the Gumbel distribution, γ is the Euler–Mascheroni constant
Euler–Mascheroni constant
The Euler–Mascheroni constant is a mathematical constant recurring in analysis and number theory, usually denoted by the lowercase Greek letter ....
0.57721… .
Extensions
Trimmed L-moments are generalizations of L-moments that give zero weight to extreme observations. They are therefore more robust to the presence of outliers, and unlike L-moments they may be well-defined for distributions for which the mean does not exist, such as the Cauchy distributionCauchy distribution
The Cauchy–Lorentz distribution, named after Augustin Cauchy and Hendrik Lorentz, is a continuous probability distribution. As a probability distribution, it is known as the Cauchy distribution, while among physicists, it is known as the Lorentz distribution, Lorentz function, or Breit–Wigner...
.
External links
- The L-moments page Jonathan R.M. Hosking, IBM ResearchIBM ResearchIBM Research, a division of IBM, is a research and advanced development organization and currently consists of eight locations throughout the world and hundreds of projects....
- L Moments. DataplotDataplotDataplot is a public-domain software system for scientific visualization and statistical analysis. It was developed at the National Institute of Standards and Technology.-External links:*...
reference manual, vol. 1, auxiliary chapter. National Institute of Standards and TechnologyNational Institute of Standards and TechnologyThe National Institute of Standards and Technology , known between 1901 and 1988 as the National Bureau of Standards , is a measurement standards laboratory, otherwise known as a National Metrological Institute , which is a non-regulatory agency of the United States Department of Commerce...
, 2006. Accessed 2010-05-25.