Gini coefficient
Overview
Italian people
The Italian people are an ethnic group that share a common Italian culture, ancestry and speak the Italian language as a mother tongue. Within Italy, Italians are defined by citizenship, regardless of ancestry or country of residence , and are distinguished from people...
statistician
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
and sociologist
Sociology
Sociology is the study of society. It is a social science—a term with which it is sometimes synonymous—which uses various methods of empirical investigation and critical analysis to develop a body of knowledge about human social activity...
Corrado Gini
Corrado Gini
Corrado Gini was an Italian statistician, demographer and sociologist who developed the Gini coefficient, a measure of the income inequality in a society. Gini was also a leading fascist theorist and ideologue who wrote The Scientific Basis of Fascism in 1927...
and published in his 1912 paper "Variability and Mutability" .
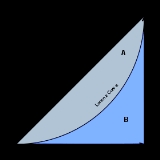
The Gini coefficient is a measure of the inequality of a distribution, a value of 0 expressing perfect equality and a value of 1 maximal inequality. It has found application in the study of inequalities in disciplines as diverse as sociology
Sociology
Sociology is the study of society. It is a social science—a term with which it is sometimes synonymous—which uses various methods of empirical investigation and critical analysis to develop a body of knowledge about human social activity...
, economics
Economics
Economics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
, health science, ecology
Ecology
Ecology is the scientific study of the relations that living organisms have with respect to each other and their natural environment. Variables of interest to ecologists include the composition, distribution, amount , number, and changing states of organisms within and among ecosystems...
, chemistry
Chemistry
Chemistry is the science of matter, especially its chemical reactions, but also its composition, structure and properties. Chemistry is concerned with atoms and their interactions with other atoms, and particularly with the properties of chemical bonds....
, engineering
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
and agriculture
Agriculture
Agriculture is the cultivation of animals, plants, fungi and other life forms for food, fiber, and other products used to sustain life. Agriculture was the key implement in the rise of sedentary human civilization, whereby farming of domesticated species created food surpluses that nurtured the...
.
It is commonly used as a measure of inequality of income
Income inequality metrics
The concept of inequality is distinct from that of poverty and fairness. Income inequality metrics or income distribution metrics are used by social scientists to measure the distribution of income, and economic inequality among the participants in a particular economy, such as that of a specific...
or wealth.

