Degrees of freedom (statistics)
Encyclopedia
In statistics
, the number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary.
Estimates of statistical parameters can be based upon different amounts of information or data. The number of independent pieces of information that go into the estimate of a parameter is called the degrees of freedom (df). In general, the degrees of freedom of an estimate of a parameter is equal to the number of independent scores that go into the estimate minus the number of parameters used as intermediate steps in the estimation of the parameter itself (which, in sample variance, is one, since the sample mean is the only intermediate step).
Mathematically, degrees of freedom is the dimension
of the domain of a random vector, or essentially the number of 'free' components: how many components need to be known before the vector is fully determined.
The term is most often used in the context of linear models (linear regression
, analysis of variance
), where certain random vectors are constrained to lie in linear subspaces, and the number of degrees of freedom is the dimension of the subspace. The degrees-of-freedom are also commonly associated with the squared lengths (or "Sum of Squares") of such vectors, and the parameters of chi-squared
and other distributions that arise in associated statistical testing problems.
While introductory texts may introduce degrees of freedom as distribution parameters or through hypothesis testing, it is the underlying geometry that defines degrees of freedom, and is critical to a proper understanding of the concept. Walker (1940) has stated this succinctly:
(lowercase Greek letter nu
). In text and tables, the abbreviation "d.f." is commonly used. R.A. Fisher used n to symbolize degrees of freedom (writing n′ for sample size) but modern usage typically reserves n for sample size.
In fitting statistical models to data, the vectors of residuals
are constrained to lie in a space of smaller dimension than the number of components in the vector. That smaller dimension is the number of degrees of freedom for error.
are random variable
s each with expected value
μ, and let
be the "sample mean." Then the quantities
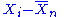
are residuals that may be considered estimates
of the errors
Xi − μ. The sum of the residuals (unlike the sum of the errors) is necessarily 0. If one knows the values of any n − 1 of the residuals, one can thus find the last one. That means they are constrained to lie in a space of dimension n − 1.
One says that "there are n − 1 degrees of freedom for residual."
An only slightly less simple example is that of least squares
estimation of a and b in the model
where εi and hence Yi are random. Let
and 
be the least-squares estimates of a and b. Then the residuals
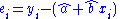
are constrained to lie within the space defined by the two equations
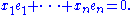
One says that there are n − 2 degrees of freedom for error.
The capital Y is used in specifying the model, and lower-case y in the definition of the residuals. That is because the former are hypothesized random variables and the latter are data.
We can generalise this to multiple regression involving p parameters and covariates (e.g. p − 1 predictors and one mean), in which case the cost in degrees of freedom of the fit is p.
.
This can be represented as an n-dimensional random vector: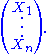
Since this random vector can lie anywhere in n-dimensional space, it has n degrees of freedom.
Now, let
be the sample mean. The random vector can be decomposed as the sum of the sample mean plus a vector of residuals:
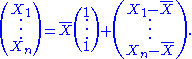
The first vector on the right-hand side is constrained to be a multiple of the vector of 1's, and the only free quantity is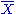
. It therefore has 1 degree of freedom.
The second vector is constrained by the relation
. The first n − 1 components of this vector can be anything. However, once you know the first n − 1 components, the constraint tells you the value of the nth component. Therefore, this vector has n − 1 degrees of freedom.
Mathematically, the first vector is the orthogonal, or least-squares, projection of the data vector onto the subspace
spanned
by the vector of 1's. The 1 degree of freedom is the dimension of this subspace. The second residual vector is the least-squares projection onto the (n − 1)-dimensional orthogonal complement of this subspace, and has n − 1 degrees of freedom.
In statistical testing applications, often one isn't directly interested in the component vectors, but rather in their squared lengths. In the example above, the residual sum-of-squares is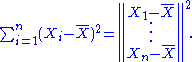
If the data points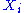
are normally distributed with mean 0 and variance 
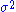, then the residual sum of squares has a scaled chi-squared distribution (scaled by the factor 
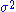), with n − 1 degrees of freedom. The degrees-of-freedom, here a parameter of the distribution, can still be interpreted as the dimension of an underlying vector subspace.
Likewise, the one-sample t-test statistic,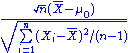
follows a Student's t distribution with n − 1 degrees of freedom when the hypothesized mean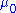
is correct. Again, the degrees-of-freedom arises from the residual vector in the denominator.
and analysis of variance
. An explicit example based on comparison of three means is presented here; the geometry of linear models is discussed in more complete detail by Christensen (2002).
Suppose independent observations are made for three populations,
, 
and 
. The restriction to three groups and equal sample sizes simplifies notation, but the ideas are easily generalized.
The observations can be decomposed as
where
are the means of the individual samples, and
is the mean of all 3n observations. In vector notation this decomposition can be written as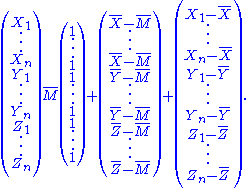
The observation vector, on the left-hand side, has 3n degrees of freedom. On the right-hand side,
the first vector has one degree of freedom (or dimension) for the overall mean. The second vector depends on three random variables,
, 
and 
. However, these must sum to 0 and so are constrained; the vector therefore must lie in a 2-dimensional subspace, and has 2 degrees of freedom. The remaining 3n − 3 degrees of freedom are in the residual vector (made up of n − 1 degrees of freedom within each of the populations).
The three-population example above is an example of one-way Analysis of Variance
. The model, or treatment, sum-of-squares is the squared length of the second vector,
with 2 degrees of freedom. The residual, or error, sum-of-squares is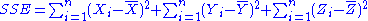
with 3(n-1) degrees of freedom. Of course, introductory books on ANOVA usually state formulae without showing the vectors, but it is this underlying geometry that gives rise to SS formulae, and shows how to unambiguously determine the degrees of freedom in any given situation.
Under the null hypothesis of no difference between population means (and assuming that standard ANOVA regularity assumptions are satisfied) the sums of squares have scaled chi-squared distributions, with the corresponding degrees of freedom. The F-test statistic is the ratio, after scaling by the degrees of freedom. If there is no difference between population means this ratio follows an F distribution with 2 and 3n − 3 degrees of freedom.
In some complicated settings, such as unbalanced split-plot designs, the sums-of-squares no longer have scaled chi-squared distributions. Comparison of sum-of-squares with degrees-of-freedom is no longer meaningful, and software may report certain fractional 'degrees of freedom' in these cases. Such numbers have no genuine degrees-of-freedom interpretation, but are simply providing an approximate chi-squared distribution for the corresponding sum-of-squares. The details of such approximations are beyond the scope of this page.
are independent normal 
random variables, the statistic
follows a chi-squared distribution with n−1 degrees of freedom. Here, the degrees of freedom arises from the residual sum-of-squares in the numerator, and in turn the n−1 degrees of freedom of the underlying residual vector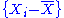
.
In the application of these distributions to linear models, the degrees of freedom parameters can take only integer
values. The underlying families of distributions allow fractional values for the degrees-of-freedom parameters, which can arise in more sophisticated uses. One set of examples is problems where chi-squared approximations based on effective degrees of freedom are used. In other applications, such as modelling heavy-tailed data, a t or F distribution may be used as an empirical model. In these cases, there is no particular degrees of freedom interpretation to the distribution parameters, even though the terminology may continue to be used.
projections, but rather on regularized
(generalized
and/or penalized) least-squares, and so degrees of freedom defined in terms of dimensionality is generally not useful for these procedures. However, these procedures are still linear in the observations, and the fitted values of the regression can be expressed in the form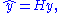
where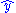
is the vector of fitted values at each of the original covariate values from the fitted model, y is the original vector of responses, and H is the hat matrix
or, more generally, smoother matrix.
For statistical inference, sums-of-squares can still be formed: the model sum-of-squares is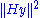
; the residual sum-of-squares is 
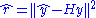. However, because H does not correspond to an ordinary least-squares fit (i.e. is not an orthogonal projection), these sums-of-squares no longer have (scaled, non-central) chi-squared distributions, and dimensionally-defined degrees-of-freedom are not useful.
The effective degrees of freedom of the fit can be defined in various ways to implement goodness-of-fit tests, cross-validation and other inferential procedures. Here one can distinguish between regression effective degrees of freedom and residual effective degrees of freedom. Regarding the former, appropriate definitions can include the trace
of the hat matrix, tr(H) ), the trace of the quadratic form of the hat matrix, tr(H'H), the form tr(2H - H H), or the Satterthwaite approximation
, . In the case of linear regression, the hat matrix H is X(X ' X)−1X ' , and all these definitions reduce to the usual degrees of freedom. Notice that
i.e., the regression (not residual) degrees of freedom in linear models are "the sum of the sensitivities of the fitted values with respect to the observed response values" ).
There are corresponding definitions of residual effective degrees-of-freedom (redf), with H replaced by I − H. For example, if the goal is to estimate error variance, the redf would be defined as tr((I − H)'(I − H)), and the unbiased estimate is (with
),
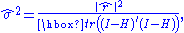
or , p.30;
, p.54; , eq.(4,14), p.172)):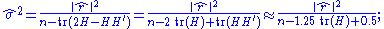
the last approximation above (derived in , eq.(B.1), p.305) reduces the computational cost from O(n2) to only O(n). In general the numerator would be the objective function being minimized; e.g., if the hat matrix includes an observation covariance matrix, Σ, then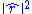
becomes 
.
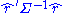Note that unlike in the original case, we allow non-integer degrees of freedom, though the value must usually still be constrained between 0 and n.
Consider, as an example, the k-nearest neighbour
smoother, which is the average of the k nearest measured values to the given point. Then, at each of the n measured points, the weight of the original value on the linear combination that makes up the predicted value is just 1/k. Thus, the trace of the hat matrix is n/k. Thus the smooth costs n/k effective degrees of freedom.
As another example, consider the existence of nearly duplicated observations. Naive application of classical formula, n - p, would lead to over-estimation of the residuals degree of freedom, as if each observation were independent. More realistically, though, the hat matrix H = X(X ' Σ−1 X)−1X ' Σ−1 would involve an observation covariance matrix Σ indicating the non-zero correlation among observations. The more general formulation of effective degree of freedom would result in a more realistic estimate for, e.g., the error variance σ2.
Similar concepts are the equivalent degrees of freedom in non-parametric regression , p.37), the degree of freedom of signal in atmospheric studies , p.31; , eq.(4.26), p.114) and the non-integer degree of freedom in geodesy , p.205), going back at least to 1963 -(5.20)).
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary.
Estimates of statistical parameters can be based upon different amounts of information or data. The number of independent pieces of information that go into the estimate of a parameter is called the degrees of freedom (df). In general, the degrees of freedom of an estimate of a parameter is equal to the number of independent scores that go into the estimate minus the number of parameters used as intermediate steps in the estimation of the parameter itself (which, in sample variance, is one, since the sample mean is the only intermediate step).
Mathematically, degrees of freedom is the dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
of the domain of a random vector, or essentially the number of 'free' components: how many components need to be known before the vector is fully determined.
The term is most often used in the context of linear models (linear regression
Linear regression
In statistics, linear regression is an approach to modeling the relationship between a scalar variable y and one or more explanatory variables denoted X. The case of one explanatory variable is called simple regression...
, analysis of variance
Analysis of variance
In statistics, analysis of variance is a collection of statistical models, and their associated procedures, in which the observed variance in a particular variable is partitioned into components attributable to different sources of variation...
), where certain random vectors are constrained to lie in linear subspaces, and the number of degrees of freedom is the dimension of the subspace. The degrees-of-freedom are also commonly associated with the squared lengths (or "Sum of Squares") of such vectors, and the parameters of chi-squared
Chi-squared
In statistics, the term chi-squared has different uses:*chi-squared distribution, a continuous probability distribution;*chi-squared statistic, a statistic used in some statistical tests;...
and other distributions that arise in associated statistical testing problems.
While introductory texts may introduce degrees of freedom as distribution parameters or through hypothesis testing, it is the underlying geometry that defines degrees of freedom, and is critical to a proper understanding of the concept. Walker (1940) has stated this succinctly:
- For the person who is unfamiliar with N-dimensional geometry or who knows the contributions to modern sampling theory only from secondhand sources such as textbooks, this concept often seems almost mystical, with no practical meaning.
Notation
In equations, the typical symbol for degrees of freedom isNu (letter)
Nu , is the 13th letter of the Greek alphabet. In the system of Greek numerals it has a value of 50...
(lowercase Greek letter nu
Nu (letter)
Nu , is the 13th letter of the Greek alphabet. In the system of Greek numerals it has a value of 50...
). In text and tables, the abbreviation "d.f." is commonly used. R.A. Fisher used n to symbolize degrees of freedom (writing n′ for sample size) but modern usage typically reserves n for sample size.
Residuals
A common way to think of degrees of freedom is as the number of independent pieces of information available to estimate another piece of information. More concretely, the number of degrees of freedom is the number of independent observations in a sample of data that are available to estimate a parameter of the population from which that sample is drawn. For example, if we have two observations, when calculating the mean we have two independent observations; however, when calculating the variance, we have only one independent observation, since the two observations are equally distant from the mean.In fitting statistical models to data, the vectors of residuals
Errors and residuals in statistics
In statistics and optimization, statistical errors and residuals are two closely related and easily confused measures of the deviation of a sample from its "theoretical value"...
are constrained to lie in a space of smaller dimension than the number of components in the vector. That smaller dimension is the number of degrees of freedom for error.
Linear regression
Perhaps the simplest example is this. Supposeare random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s each with expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
μ, and let
be the "sample mean." Then the quantities
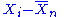
are residuals that may be considered estimates
Estimation theory
Estimation theory is a branch of statistics and signal processing that deals with estimating the values of parameters based on measured/empirical data that has a random component. The parameters describe an underlying physical setting in such a way that their value affects the distribution of the...
of the errors
Errors and residuals in statistics
In statistics and optimization, statistical errors and residuals are two closely related and easily confused measures of the deviation of a sample from its "theoretical value"...
Xi − μ. The sum of the residuals (unlike the sum of the errors) is necessarily 0. If one knows the values of any n − 1 of the residuals, one can thus find the last one. That means they are constrained to lie in a space of dimension n − 1.
One says that "there are n − 1 degrees of freedom for residual."
An only slightly less simple example is that of least squares
Least squares
The method of least squares is a standard approach to the approximate solution of overdetermined systems, i.e., sets of equations in which there are more equations than unknowns. "Least squares" means that the overall solution minimizes the sum of the squares of the errors made in solving every...
estimation of a and b in the model
where εi and hence Yi are random. Let
and be the least-squares estimates of a and b. Then the residuals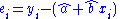are constrained to lie within the space defined by the two equations
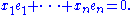
One says that there are n − 2 degrees of freedom for error.
The capital Y is used in specifying the model, and lower-case y in the definition of the residuals. That is because the former are hypothesized random variables and the latter are data.
We can generalise this to multiple regression involving p parameters and covariates (e.g. p − 1 predictors and one mean), in which case the cost in degrees of freedom of the fit is p.
Degrees of freedom of a random vector
Geometrically, the degrees of freedom can be interpreted as the dimension of certain vector subspaces. As a starting point, suppose that we have a sample of n independent normally distributed observations,.This can be represented as an n-dimensional random vector:
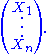
Since this random vector can lie anywhere in n-dimensional space, it has n degrees of freedom.
Now, let
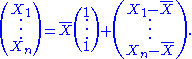
be the sample mean. The random vector can be decomposed as the sum of the sample mean plus a vector of residuals:The first vector on the right-hand side is constrained to be a multiple of the vector of 1's, and the only free quantity is
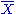. It therefore has 1 degree of freedom.The second vector is constrained by the relation
. The first n − 1 components of this vector can be anything. However, once you know the first n − 1 components, the constraint tells you the value of the nth component. Therefore, this vector has n − 1 degrees of freedom.Mathematically, the first vector is the orthogonal, or least-squares, projection of the data vector onto the subspace
Euclidean subspace
In linear algebra, a Euclidean subspace is a set of vectors that is closed under addition and scalar multiplication. Geometrically, a subspace is a flat in n-dimensional Euclidean space that passes through the origin...
spanned
Linear span
In the mathematical subfield of linear algebra, the linear span of a set of vectors in a vector space is the intersection of all subspaces containing that set...
by the vector of 1's. The 1 degree of freedom is the dimension of this subspace. The second residual vector is the least-squares projection onto the (n − 1)-dimensional orthogonal complement of this subspace, and has n − 1 degrees of freedom.
In statistical testing applications, often one isn't directly interested in the component vectors, but rather in their squared lengths. In the example above, the residual sum-of-squares is
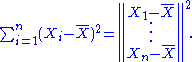
If the data points
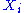are normally distributed with mean 0 and variance 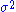, then the residual sum of squares has a scaled chi-squared distribution (scaled by the factor 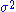), with n − 1 degrees of freedom. The degrees-of-freedom, here a parameter of the distribution, can still be interpreted as the dimension of an underlying vector subspace.Likewise, the one-sample t-test statistic,
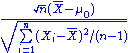
follows a Student's t distribution with n − 1 degrees of freedom when the hypothesized mean
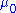is correct. Again, the degrees-of-freedom arises from the residual vector in the denominator.Degrees of freedom in linear models
The demonstration of the t and chi-squared distributions for one-sample problems above is the simplest example where degrees-of-freedom arise. However, similar geometry and vector decompositions underlie much of the theory of linear models, including linear regressionLinear regression
In statistics, linear regression is an approach to modeling the relationship between a scalar variable y and one or more explanatory variables denoted X. The case of one explanatory variable is called simple regression...
and analysis of variance
Analysis of variance
In statistics, analysis of variance is a collection of statistical models, and their associated procedures, in which the observed variance in a particular variable is partitioned into components attributable to different sources of variation...
. An explicit example based on comparison of three means is presented here; the geometry of linear models is discussed in more complete detail by Christensen (2002).
Suppose independent observations are made for three populations,
, and . The restriction to three groups and equal sample sizes simplifies notation, but the ideas are easily generalized.The observations can be decomposed as
where
are the means of the individual samples, and is the mean of all 3n observations. In vector notation this decomposition can be written as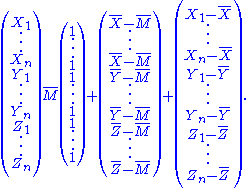The observation vector, on the left-hand side, has 3n degrees of freedom. On the right-hand side,
the first vector has one degree of freedom (or dimension) for the overall mean. The second vector depends on three random variables,
, and . However, these must sum to 0 and so are constrained; the vector therefore must lie in a 2-dimensional subspace, and has 2 degrees of freedom. The remaining 3n − 3 degrees of freedom are in the residual vector (made up of n − 1 degrees of freedom within each of the populations).Sum of squares and degrees of freedom
In statistical testing problems, one usually isn't interested in the component vectors themselves, but rather in their squared lengths, or Sum of Squares. The degrees of freedom associated with a sum-of-squares is the degrees-of-freedom of the corresponding component vectors.The three-population example above is an example of one-way Analysis of Variance
One-way ANOVA
In statistics, one-way analysis of variance is a technique used to compare means of two or more samples . This technique can be used only for numerical data....
. The model, or treatment, sum-of-squares is the squared length of the second vector,
with 2 degrees of freedom. The residual, or error, sum-of-squares is
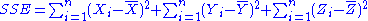
with 3(n-1) degrees of freedom. Of course, introductory books on ANOVA usually state formulae without showing the vectors, but it is this underlying geometry that gives rise to SS formulae, and shows how to unambiguously determine the degrees of freedom in any given situation.
Under the null hypothesis of no difference between population means (and assuming that standard ANOVA regularity assumptions are satisfied) the sums of squares have scaled chi-squared distributions, with the corresponding degrees of freedom. The F-test statistic is the ratio, after scaling by the degrees of freedom. If there is no difference between population means this ratio follows an F distribution with 2 and 3n − 3 degrees of freedom.
In some complicated settings, such as unbalanced split-plot designs, the sums-of-squares no longer have scaled chi-squared distributions. Comparison of sum-of-squares with degrees-of-freedom is no longer meaningful, and software may report certain fractional 'degrees of freedom' in these cases. Such numbers have no genuine degrees-of-freedom interpretation, but are simply providing an approximate chi-squared distribution for the corresponding sum-of-squares. The details of such approximations are beyond the scope of this page.
Degrees of freedom parameters in probability distributions
Several commonly encountered statistical distributions (Student's t, Chi-Squared, F) have parameters that are commonly referred to as degrees of freedom. This terminology simply reflects that in many applications where these distributions occur, the parameter corresponds to the degrees of freedom of an underlying random vector, as in the preceding ANOVA example. Another simple example is: if are independent normal random variables, the statisticfollows a chi-squared distribution with n−1 degrees of freedom. Here, the degrees of freedom arises from the residual sum-of-squares in the numerator, and in turn the n−1 degrees of freedom of the underlying residual vector
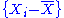.In the application of these distributions to linear models, the degrees of freedom parameters can take only integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
values. The underlying families of distributions allow fractional values for the degrees-of-freedom parameters, which can arise in more sophisticated uses. One set of examples is problems where chi-squared approximations based on effective degrees of freedom are used. In other applications, such as modelling heavy-tailed data, a t or F distribution may be used as an empirical model. In these cases, there is no particular degrees of freedom interpretation to the distribution parameters, even though the terminology may continue to be used.
Effective degrees of freedom
Many regression methods, including ridge regression, linear smoothers and smoothing splines are not based on ordinary least squaresOrdinary least squares
In statistics, ordinary least squares or linear least squares is a method for estimating the unknown parameters in a linear regression model. This method minimizes the sum of squared vertical distances between the observed responses in the dataset and the responses predicted by the linear...
projections, but rather on regularized
Regularization (mathematics)
In mathematics and statistics, particularly in the fields of machine learning and inverse problems, regularization involves introducing additional information in order to solve an ill-posed problem or to prevent overfitting...
(generalized
Generalized least squares
In statistics, generalized least squares is a technique for estimating the unknown parameters in a linear regression model. The GLS is applied when the variances of the observations are unequal , or when there is a certain degree of correlation between the observations...
and/or penalized) least-squares, and so degrees of freedom defined in terms of dimensionality is generally not useful for these procedures. However, these procedures are still linear in the observations, and the fitted values of the regression can be expressed in the form
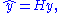
where
is the vector of fitted values at each of the original covariate values from the fitted model, y is the original vector of responses, and H is the hat matrixHat matrix
In statistics, the hat matrix, H, maps the vector of observed values to the vector of fitted values. It describes the influence each observed value has on each fitted value...
or, more generally, smoother matrix.
For statistical inference, sums-of-squares can still be formed: the model sum-of-squares is
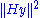; the residual sum-of-squares is 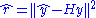. However, because H does not correspond to an ordinary least-squares fit (i.e. is not an orthogonal projection), these sums-of-squares no longer have (scaled, non-central) chi-squared distributions, and dimensionally-defined degrees-of-freedom are not useful.The effective degrees of freedom of the fit can be defined in various ways to implement goodness-of-fit tests, cross-validation and other inferential procedures. Here one can distinguish between regression effective degrees of freedom and residual effective degrees of freedom. Regarding the former, appropriate definitions can include the trace
Trace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
of the hat matrix, tr(H) ), the trace of the quadratic form of the hat matrix, tr(H'H), the form tr(2H - H H), or the Satterthwaite approximation
Welch-Satterthwaite equation
In statistics and uncertainty analysis, the Welch–Satterthwaite equation is used to calculate an approximation to the effective degrees of freedom of a linear combination of independent sample variances....
, . In the case of linear regression, the hat matrix H is X(X
i.e., the regression (not residual) degrees of freedom in linear models are "the sum of the sensitivities of the fitted values with respect to the observed response values" ).
There are corresponding definitions of residual effective degrees-of-freedom (redf), with H replaced by I − H. For example, if the goal is to estimate error variance, the redf would be defined as tr((I − H)'(I − H)), and the unbiased estimate is (with
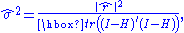
),or , p.30;
, p.54; , eq.(4,14), p.172)):
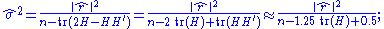
the last approximation above (derived in , eq.(B.1), p.305) reduces the computational cost from O(n2) to only O(n). In general the numerator would be the objective function being minimized; e.g., if the hat matrix includes an observation covariance matrix, Σ, then
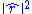becomes 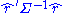.Note that unlike in the original case, we allow non-integer degrees of freedom, though the value must usually still be constrained between 0 and n.
Consider, as an example, the k-nearest neighbour
K-nearest neighbor algorithm
In pattern recognition, the k-nearest neighbor algorithm is a method for classifying objects based on closest training examples in the feature space. k-NN is a type of instance-based learning, or lazy learning where the function is only approximated locally and all computation is deferred until...
smoother, which is the average of the k nearest measured values to the given point. Then, at each of the n measured points, the weight of the original value on the linear combination that makes up the predicted value is just 1/k. Thus, the trace of the hat matrix is n/k. Thus the smooth costs n/k effective degrees of freedom.
As another example, consider the existence of nearly duplicated observations. Naive application of classical formula, n - p, would lead to over-estimation of the residuals degree of freedom, as if each observation were independent. More realistically, though, the hat matrix H = X(X
Similar concepts are the equivalent degrees of freedom in non-parametric regression , p.37), the degree of freedom of signal in atmospheric studies , p.31; , eq.(4.26), p.114) and the non-integer degree of freedom in geodesy , p.205), going back at least to 1963 -(5.20)).
See also
- VarianceVarianceIn probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
- Sample sizeSample sizeSample size determination is the act of choosing the number of observations to include in a statistical sample. The sample size is an important feature of any empirical study in which the goal is to make inferences about a population from a sample...
- Replication (statistics)Replication (statistics)In engineering, science, and statistics, replication is the repetition of an experimental condition so that the variability associated with the phenomenon can be estimated. ASTM, in standard E1847, defines replication as "the repetition of the set of all the treatment combinations to be compared in...
External links
- Walker, HW (1940) "Degrees of Freedom" Journal of Educational Psychology 31(4) 253-269. Transcription by C Olsen with errata
- Yu, Chong-ho (1997) Illustrating degrees of freedom in terms of sample size and dimensionality
- Dallal, GE. (2003) Degrees of Freedom