
Mean difference
Encyclopedia
The mean difference is a measure of statistical dispersion equal to the average absolute difference
of two independent values drawn from a probability distribution. A related statistic is the relative mean difference, which is the mean difference divided by the arithmetic mean
. An important relationship is that the relative mean difference is equal to twice the Gini coefficient
, which is defined in terms of the Lorenz curve
.
The mean difference is also known as the absolute mean difference and the Gini
mean difference. The mean difference is sometimes denoted by Δ or as MD. The mean deviation is a different measure of dispersion.
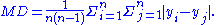
For a discrete probability function f(y), where yi, i = 1 to n, are the values with nonzero probabilities:
For a probability density function
f(x):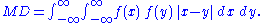
For a cumulative distribution function
F(x) with quantile function
F(x):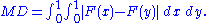
, the relative mean difference, sometimes denoted by ∇ or RMD, is defined by

The relative mean difference quantifies the mean difference in comparison to the size of the mean and is a dimensionless quantity. The relative mean difference is equal to twice the Gini coefficient
which is defined in terms of the Lorenz curve
. This relationship gives complementary perspectives to both the relative mean difference and the Gini coefficient, including alternative ways of calculating their values.
The relative mean difference is invariant to positive scaling, commutes with negation, and varies under translation in proportion to the ratio of the original and translated arithmetic means. That is to say, if X is a random variable and c is a constant:
If a random variable has a positive mean, then its relative mean difference will always be greater than or equal to zero. If, additionally, the random variable can only take on values that are greater than or equal to zero, then its relative mean difference will be less than 2.
and the mean difference measure dispersion—how spread out are the values of a population or the probabilities of a distribution. The mean difference is not defined in terms of a specific measure of central tendency, whereas the standard deviation is defined in terms of the deviation from the arithmetic mean. Because the standard deviation squares its differences, it tends to give more weight to larger differences and less weight to smaller differences compared to the mean difference. When the arithmetic mean is finite, the mean difference will also be finite, even when the standard deviation is infinite. See the examples for some specific comparisons. The recently introduced distance standard deviation plays similar role than the mean difference but the distance standard deviation works with centered distances. See also E-statistics.
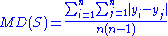
is a consistent and unbiased estimator
of MD(X). The statistic: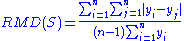
is a consistent estimator
of RMD(X), but is not, in general, unbiased.
Confidence intervals for RMD(X) can be calculated using bootstrap sampling techniques.
There does not exist, in general, an unbiased estimator for RMD(X), in part because of the difficulty of finding an unbiased estimation for multiplying by the inverse of the mean. For example, even where the sample is known to be taken from a random variable X(p) for an unknown p, and X(p) - 1 has the Bernoulli distribution, so that Pr(X(p) = 1) = 1 − p and , then
But the expected value of any estimator R(S) of RMD(X(p)) will be of the form:
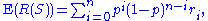
where the r i are constants. So E(R(S)) can never equal RMD(X(p)) for all p between 0 and 1.
Absolute difference
The absolute difference of two real numbers x, y is given by |x − y|, the absolute value of their difference. It describes the distance on the real line between the points corresponding to x and y...
of two independent values drawn from a probability distribution. A related statistic is the relative mean difference, which is the mean difference divided by the arithmetic mean
Arithmetic mean
In mathematics and statistics, the arithmetic mean, often referred to as simply the mean or average when the context is clear, is a method to derive the central tendency of a sample space...
. An important relationship is that the relative mean difference is equal to twice the Gini coefficient
Gini coefficient
The Gini coefficient is a measure of statistical dispersion developed by the Italian statistician and sociologist Corrado Gini and published in his 1912 paper "Variability and Mutability" ....
, which is defined in terms of the Lorenz curve
Lorenz curve
In economics, the Lorenz curve is a graphical representation of the cumulative distribution function of the empirical probability distribution of wealth; it is a graph showing the proportion of the distribution assumed by the bottom y% of the values...
.
The mean difference is also known as the absolute mean difference and the Gini
Corrado Gini
Corrado Gini was an Italian statistician, demographer and sociologist who developed the Gini coefficient, a measure of the income inequality in a society. Gini was also a leading fascist theorist and ideologue who wrote The Scientific Basis of Fascism in 1927...
mean difference. The mean difference is sometimes denoted by Δ or as MD. The mean deviation is a different measure of dispersion.
Calculation
For a population of size n, with a sequence of values yi, i = 1 to n: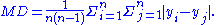
For a discrete probability function f(y), where yi, i = 1 to n, are the values with nonzero probabilities:

For a probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
f(x):
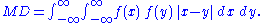
For a cumulative distribution function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
F(x) with quantile function
Quantile function
In probability and statistics, the quantile function of the probability distribution of a random variable specifies, for a given probability, the value which the random variable will be at, or below, with that probability...
F(x):
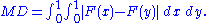
Relative mean difference
When the probability distribution has a finite and nonzero arithmetic meanArithmetic mean
In mathematics and statistics, the arithmetic mean, often referred to as simply the mean or average when the context is clear, is a method to derive the central tendency of a sample space...
, the relative mean difference, sometimes denoted by ∇ or RMD, is defined by

The relative mean difference quantifies the mean difference in comparison to the size of the mean and is a dimensionless quantity. The relative mean difference is equal to twice the Gini coefficient
Gini coefficient
The Gini coefficient is a measure of statistical dispersion developed by the Italian statistician and sociologist Corrado Gini and published in his 1912 paper "Variability and Mutability" ....
which is defined in terms of the Lorenz curve
Lorenz curve
In economics, the Lorenz curve is a graphical representation of the cumulative distribution function of the empirical probability distribution of wealth; it is a graph showing the proportion of the distribution assumed by the bottom y% of the values...
. This relationship gives complementary perspectives to both the relative mean difference and the Gini coefficient, including alternative ways of calculating their values.
Properties
The mean difference is invariant to translations and negation, and varies proportionally to positive scaling. That is to say, if X is a random variable and c is a constant:- MD(X + c) = MD(X),
- MD(-X) = MD(X), and
- MD(c X) = |c| MD(X).
The relative mean difference is invariant to positive scaling, commutes with negation, and varies under translation in proportion to the ratio of the original and translated arithmetic means. That is to say, if X is a random variable and c is a constant:
- RMD(X + c) = RMD(X) · mean(X)/(mean(X) + c) = RMD(X) / (1+c / mean(X)) for c ≠ -mean(X),
- RMD(-X) = −RMD(X), and
- RMD(c X) = RMD(X) for c > 0.
If a random variable has a positive mean, then its relative mean difference will always be greater than or equal to zero. If, additionally, the random variable can only take on values that are greater than or equal to zero, then its relative mean difference will be less than 2.
Compared to standard deviation
Both the standard deviationStandard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
and the mean difference measure dispersion—how spread out are the values of a population or the probabilities of a distribution. The mean difference is not defined in terms of a specific measure of central tendency, whereas the standard deviation is defined in terms of the deviation from the arithmetic mean. Because the standard deviation squares its differences, it tends to give more weight to larger differences and less weight to smaller differences compared to the mean difference. When the arithmetic mean is finite, the mean difference will also be finite, even when the standard deviation is infinite. See the examples for some specific comparisons. The recently introduced distance standard deviation plays similar role than the mean difference but the distance standard deviation works with centered distances. See also E-statistics.
Sample estimators
For a random sample S from a random variable X, consisting of n values yi, the statistic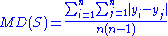
is a consistent and unbiased estimator
Estimator
In statistics, an estimator is a rule for calculating an estimate of a given quantity based on observed data: thus the rule and its result are distinguished....
of MD(X). The statistic:
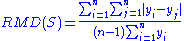
is a consistent estimator
Estimator
In statistics, an estimator is a rule for calculating an estimate of a given quantity based on observed data: thus the rule and its result are distinguished....
of RMD(X), but is not, in general, unbiased.
Confidence intervals for RMD(X) can be calculated using bootstrap sampling techniques.
There does not exist, in general, an unbiased estimator for RMD(X), in part because of the difficulty of finding an unbiased estimation for multiplying by the inverse of the mean. For example, even where the sample is known to be taken from a random variable X(p) for an unknown p, and X(p) - 1 has the Bernoulli distribution, so that Pr(X(p) = 1) = 1 − p and , then
- RMD(X(p)) = 2p(1 − p)/(1 + p).
But the expected value of any estimator R(S) of RMD(X(p)) will be of the form:
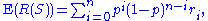
where the r i are constants. So E(R(S)) can never equal RMD(X(p)) for all p between 0 and 1.
Examples
| Distribution | Parameters | Mean | Standard Deviation | Mean Difference | Relative Mean Difference |
|---|---|---|---|---|---|
| Continuous uniform Uniform distribution (continuous) In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by... |
a = 0 ; b = 1 | 1 / 2 = 0.5 |  ≈ 0.2887 ≈ 0.2887 |
1 / 3 ≈ 0.3333 | 2 / 3 ≈ 0.6667 |
| Normal | μ = 1 ; σ = 1 | 1 | 1 | 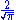 ≈ 1.1284 ≈ 1.1284 |
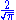 ≈ 1.1284 ≈ 1.1284 |
| Exponential Exponential distribution In probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e... |
λ = 1 | 1 | 1 | 1 | 1 |
| Pareto | k > 1 ; xm = 1 | 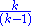 |
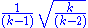 (for k > 2) (for k > 2) |
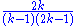 |
 |
| Gamma | k ; θ | kθ | 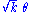 |
k θ (2 − 4 I 0.5 (k+1 , k)) † | 2 − 4 I 0.5 (k+1 , k) † |
| Gamma | k = 1 ; θ = 1 | 1 | 1 | 1 | 1 |
| Gamma | k = 2 ; θ = 1 | 2 |  ≈ 1.4142 ≈ 1.4142 |
3 / 2 = 1.5 | 3 / 4 = 0.75 |
| Gamma | k = 3 ; θ = 1 | 3 |  ≈ 1.7321 ≈ 1.7321 |
15 / 8 = 1.875 | 5 / 8 = 0.625 |
| Gamma | k = 4 ; θ = 1 | 4 | 2 | 35 / 16 = 2.1875 | 35 / 64 = 0.546875 |
| Bernoulli | 0 ≤ p ≤ 1 | p | 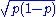 |
2 p (1 − p) | 2 (1 − p) for p > 0 |
| Student's t, 2 d.f. Degrees of freedom (statistics) In statistics, the number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary.Estimates of statistical parameters can be based upon different amounts of information or data. The number of independent pieces of information that go into the... |
ν = 2 | 0 |  |
π / √2 = 2.2214 | undefined |
- † I z (x,y) is the regularized incomplete Beta function
See also
- Mean Deviation
- EstimatorEstimatorIn statistics, an estimator is a rule for calculating an estimate of a given quantity based on observed data: thus the rule and its result are distinguished....
- Coefficient of variationCoefficient of variationIn probability theory and statistics, the coefficient of variation is a normalized measure of dispersion of a probability distribution. It is also known as unitized risk or the variation coefficient. The absolute value of the CV is sometimes known as relative standard deviation , which is...
- L-momentL-momentIn statistics, L-moments are statistics used to summarize the shape of a probability distribution. They are analogous to conventional moments in that they can be used to calculate quantities analogous to standard deviation, skewness and kurtosis, termed the L-scale, L-skewness and L-kurtosis...

