Quotient algebra
Encyclopedia
In mathematics
, a quotient algebra, (where algebra is used in the sense of universal algebra
), also called a factor algebra is obtained by partitioning the elements of an algebra in equivalence classes given by a congruence
, that is an equivalence relation
that is additionally compatible with all the operations
of the algebra, in the formal sense described below.
), and let E be an equivalence relation on the set A. The relation E is said to be compatible with (or have the substitution property with respect to) an n-ary operation f if for all 
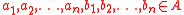whenever 
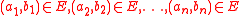implies 
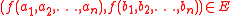. An equivalence relation compatible with all the operations of an algebra is called a congruence.
on the set A, the identity relation on A, and 
are trivial congruences. An algebra with no other congruences is called simple.
Let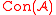
be the set of congruences on the algebra 
. Because congruences are closed under intersection, we can define a meet operation
:
by simply taking the intersection of the congruences 
.
On the other hand, congruences are not closed under union. However, we can define the closure
of any binary relation
E, with respect to a fixed algebra
, such that it is a congruence, in the following way: 
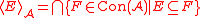. Note that the (congruence) closure of a binary relation depends on the operations in 
, not just on the carrier set. Now define 
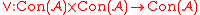as 
.
For every algebra
, 
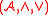with the two operations defined above forms a lattice
, called the congruence lattice of
.
, it is straightforward to defined the operations induced on A/E if E is a congruence. Specifically, for any operation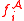 
of arity
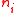in 
(where the superscript simply denotes that it's an operation in 
) define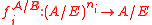 
as 
, where 
denotes the equivalence class of a modulo E.
For an algebra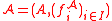
, given a congruence E on 
, the algebra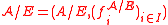 
is called the quotient algebra (or factor algebra) of 
modulo E. There is a natural homomorphism
from
to 
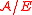mapping every element to its equivalence class. In fact, every homomorphism h determines a congruence relation; the kernel of the homomorphism, 
.
Given an algebra
, a homomorphism h thus defines two algebras homomorphic to 
, the image
h(
) and 
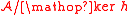The two are isomorphic, a result known as the homomorphic image theorem. Formally, let 
be a surjective homomorphism. Then, there exists a unique isomorphism g from 
onto 
such that g composed
with the natural homomorphism induced by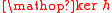
equals h.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a quotient algebra, (where algebra is used in the sense of universal algebra
Universal algebra
Universal algebra is the field of mathematics that studies algebraic structures themselves, not examples of algebraic structures....
), also called a factor algebra is obtained by partitioning the elements of an algebra in equivalence classes given by a congruence
Congruence
Congruence is the state achieved by coming together, the state of agreement. The Latin congruō meaning “I meet together, I agree”. As an abstract term, congruence means similarity between objects...
, that is an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
that is additionally compatible with all the operations
Operation (mathematics)
The general operation as explained on this page should not be confused with the more specific operators on vector spaces. For a notion in elementary mathematics, see arithmetic operation....
of the algebra, in the formal sense described below.
Compatible operation
Let A be a set (of the elements of an algebra), and let E be an equivalence relation on the set A. The relation E is said to be compatible with (or have the substitution property with respect to) an n-ary operation f if for all 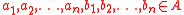whenever 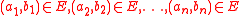implies 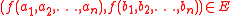. An equivalence relation compatible with all the operations of an algebra is called a congruence.Congruence lattice
For every algebra on the set A, the identity relation on A, and are trivial congruences. An algebra with no other congruences is called simple.Let
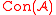be the set of congruences on the algebra . Because congruences are closed under intersection, we can define a meet operationMeet (mathematics)
In mathematics, join and meet are dual binary operations on the elements of a partially ordered set. A join on a set is defined as the supremum with respect to a partial order on the set, provided a supremum exists...
:
by simply taking the intersection of the congruences .On the other hand, congruences are not closed under union. However, we can define the closure
Closure operator
In mathematics, a closure operator on a set S is a function cl: P → P from the power set of S to itself which satisfies the following conditions for all sets X,Y ⊆ S....
of any binary relation
Binary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
E, with respect to a fixed algebra
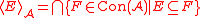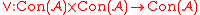, such that it is a congruence, in the following way: . Note that the (congruence) closure of a binary relation depends on the operations in , not just on the carrier set. Now define as .For every algebra
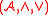, with the two operations defined above forms a latticeLattice (order)
In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
, called the congruence lattice of
.Quotient algebras and homomorphisms
A set A can be partitioned in equivalence classes given by an equivalence relation E, and usually called a quotient set, and denoted A/E. For an algebra, it is straightforward to defined the operations induced on A/E if E is a congruence. Specifically, for any operation 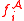of arityArity
In logic, mathematics, and computer science, the arity of a function or operation is the number of arguments or operands that the function takes. The arity of a relation is the dimension of the domain in the corresponding Cartesian product...
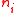in (where the superscript simply denotes that it's an operation in ) define 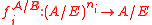as , where denotes the equivalence class of a modulo E.For an algebra
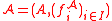, given a congruence E on , the algebra 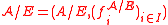is called the quotient algebra (or factor algebra) of modulo E. There is a natural homomorphismHomomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
from
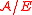to mapping every element to its equivalence class. In fact, every homomorphism h determines a congruence relation; the kernel of the homomorphism, .Given an algebra
, a homomorphism h thus defines two algebras homomorphic to , the imageImage (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
h(
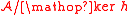) and The two are isomorphic, a result known as the homomorphic image theorem. Formally, let be a surjective homomorphism. Then, there exists a unique isomorphism g from onto such that g composedFunction composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
with the natural homomorphism induced by
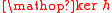equals h.