
Semigroup with involution
Encyclopedia
In mathematics
, in semigroup theory, an involution in a semigroup
is a transformation of the semigroup which is its own inverse
and which is an anti-automorphism of the semigroup. A semigroup in which an involution is defined is called a semigroup with involution. In the multiplicative
semigroup of real
square matrices
of order n, the map
which sends a matrix to its transpose
is an involution. In the free semigroup
generated by a nonempty set the operation
which reverse
s the order
of the letters in a word is an involution. A semigroup with an involution is also called a *– semigroup.
* on S (or, a transformation * : S → S, x → x*) satisfying the following conditions:
The semigroup S with the involution * is called a semigroup with involution.
Partial isometries can be partially ordered by s ≤ t if and only if
s = ss*t and ss* = ss*tt*. Equivalently, s ≤ t if and only if s = et and e = ett* for some projection e. In a *-semigroup, PI(S) is an ordered groupoid with the partial product given by s•t = st if s*s = tt*.
The partial isometries
in a C*-algebra are exactly those defined in this section. In the case of Mn(C) more can be said. If E and F are projections, then E ≤ F if and only if im
E ⊆ imF. For any two projection, if E ∩ F = V, then the unique projection J with image V and kernel the orthogonal complement of V is the meet of E and F. Since projections form a meet-semilattice
, the partial isometries on Mn(C) form an inverse semigroup with the product .
.
H. This defining property can be formulated in several equivalent ways. Another is to say that every L-class contains a projection. An axiomatic definition is the condition that for every x in S there exists an element x’ such that x’xx’ = x’, xx’x = x, ( xx’ )* = xx’, ( x’x )* = x’x. Michael P. Drazin
first proved that given x, the element x’ satisfying these axioms is unique. It is called the Moore–Penrose inverse of x. This agrees with the classical definition of the Moore–Penrose inverse of a square matrix.
In the multiplicative
semigroup Mn ( C ) of square matrices of order n, the map which assigns a matrix A to its Hermitian conjugate A* is an involution. The semigroup Mn ( C ) is a * – regular semigroup with this involution. The Moore–Penrose inverse of A in this * – regular semigroup is the classical Moore–Penrose inverse of A.
is a *-regular semigroup. The following characterization was given by M. Yamada. Define a P-system F(S) as subset of the idempotents of S, denoted as usual by E(S). Using the usual notation V(a) for the inverses of a, F(S) needs to satisfy the following axioms:
A regular semigroup S is a *-regular semigroup, as defined by Nordahl & Scheiblich, if and only if it has a p-system F(S). In this case F(S) is the set of projections of S with respect to the operation ° defined by F(S). In an inverse semigroup
the entire semilattice of idempotents is a p-system. Also, if a regular semigroup S has a p-system that is multiplicatively closed (i.e. subsemigroup), then S is an inverse semigroup. Thus, a p-system may be regarded as a generalization of the semilattice of idempotents of an inverse semigroup.
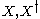 be two disjoint sets in bijective correspondence
be two disjoint sets in bijective correspondence
given by the map
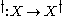 .
.
Denote by (here we use instead of
instead of  to remind that the union is actually a disjoint union
to remind that the union is actually a disjoint union
)
and by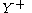 the free semigroup
the free semigroup
on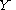 . We can extend the map
. We can extend the map
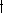 to a map
to a map
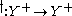
in the following way: given for some letters
for some letters 
then we define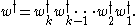
This map
is an involution on the semigroup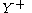 . This is the only way to extend the map
. This is the only way to extend the map 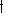 from
from 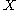 to
to 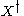 , to an involution on
, to an involution on 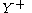 .
.
Thus, the semigroup with the map
with the map  is a semigroup with involution. Moreover, it is the free semigroup with involution on
is a semigroup with involution. Moreover, it is the free semigroup with involution on 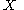 in the sense that it solves the following universal problem
in the sense that it solves the following universal problem
: given a semigroup with involution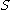 and a map
and a map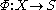 ,
,
a semigroup homomorphism
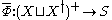
exists such that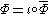
where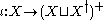
is the inclusion map
and composition of functions is taken in the diagram order.
It is well known from universal algebra
that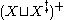 is unique up to isomorphism
is unique up to isomorphism
s.
If we use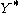 instead of
instead of 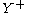 , where
, where
where is the empty word (the identity
is the empty word (the identity
of the monoid
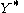 ), we obtain a monoid
), we obtain a monoid
with involution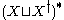 that is the free monoid with involution on
that is the free monoid with involution on 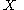 .
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in semigroup theory, an involution in a semigroup
Semigroup
In mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
is a transformation of the semigroup which is its own inverse
Inverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
and which is an anti-automorphism of the semigroup. A semigroup in which an involution is defined is called a semigroup with involution. In the multiplicative
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
semigroup of real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
square matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
of order n, the map
Map (mathematics)
In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
which sends a matrix to its transpose
Transpose
In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...
is an involution. In the free semigroup
Free semigroup
In abstract algebra, the free monoid on a set A is the monoid whose elements are all the finite sequences of zero or more elements from A. It is usually denoted A∗. The identity element is the unique sequence of zero elements, often called the empty string and denoted by ε or λ, and the...
generated by a nonempty set the operation
Operation (mathematics)
The general operation as explained on this page should not be confused with the more specific operators on vector spaces. For a notion in elementary mathematics, see arithmetic operation....
which reverse
Reverse
Reverse may refer to:*The reverse side of currency or a flag; see Obverse and reverse*A change in the direction of:**the movement of a motor or other prime mover; see Transmission **an engineering design: see Reverse engineering...
s the order
Order theory
Order theory is a branch of mathematics which investigates our intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and gives some basic definitions...
of the letters in a word is an involution. A semigroup with an involution is also called a *– semigroup.
Formal definition
Let S be a semigroup. An involution in S is a unary operationUnary operation
In mathematics, a unary operation is an operation with only one operand, i.e. a single input. Specifically, it is a functionf:\ A\to Awhere A is a set. In this case f is called a unary operation on A....
* on S (or, a transformation * : S → S, x → x*) satisfying the following conditions:
- For all x in S, (x*)* = x.
- For all x, y in S we have ( xy )* = y*x*.
The semigroup S with the involution * is called a semigroup with involution.
Examples
- If S is a commutative semigroup then the identity mapIdentity functionIn mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
of S is an involution. - If S is a groupGroup (mathematics)In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
then the inversion map * : S → S defined by x* = x−1 is an involution. - If S is an inverse semigroupInverse semigroupIn mathematics, an inverse semigroup S is a semigroup in which every element x in S has a unique inversey in S in the sense that x = xyx and y = yxy...
then the inversion map is an involution which leaves the idempotents invariantInvariant (mathematics)In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
. The inversion map is not necessarily the only map with this property in an inverse semigroup; there may well be other involutions that leave all idempotents invariant. A regular semigroupRegular semigroupA regular semigroup is a semigroup S in which every element is regular, i.e., for each element a, there exists an element x such that axa = a. Regular semigroups are one of the most-studied classes of semigroups, and their structure is particularly amenable to study via Green's relations.- Origins...
is an inverse semigroupInverse semigroupIn mathematics, an inverse semigroup S is a semigroup in which every element x in S has a unique inversey in S in the sense that x = xyx and y = yxy...
if and only if it admits an involution under which each idempotent is an invariant. - Underlying every C*-algebra is a *-semigroup. An important instance is the algebra Mn(C) of n-by-n matricesMatrix (mathematics)In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
over CComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
. - If X is a set, the set of all binary relationBinary relationIn mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
s on X is a *-semigroup with the * given by the inverse relationInverse relationIn mathematics, the inverse relation of a binary relation is the relation that occurs when you switch the order of the elements in the relation. For example, the inverse of the relation 'child of' is the relation 'parent of'...
, and the multiplication given by the usual composition of relationsComposition of relationsIn mathematics, the composition of binary relations is a concept of forming a new relation from two given relations R and S, having as its most well-known special case the composition of functions.- Definition :...
.
Basic concepts and properties
Certain basic concepts may be defined on *-semigroups in a way that parallels the notions stemming from a (von Neumann) regular element in a semigroup. A partial isometry is an element s when ss*s = s; the set of partial isometries is usually abbreviated PI(S). A projection is an idempotent element e that is fixed by the involution, i.e. ee = e and e* = e. Every projection is a partial isometry, and for every partial isometry s, s*s and ss* are projections. If e and f are projections, then e = ef if and only if e = fe.Partial isometries can be partially ordered by s ≤ t if and only if
IFF
IFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
s = ss*t and ss* = ss*tt*. Equivalently, s ≤ t if and only if s = et and e = ett* for some projection e. In a *-semigroup, PI(S) is an ordered groupoid with the partial product given by s•t = st if s*s = tt*.
The partial isometries
Partial isometry
In functional analysis a partial isometry is a linear map W between Hilbert spaces H and K such that the restriction of W to the orthogonal complement of its kernel is an isometry...
in a C*-algebra are exactly those defined in this section. In the case of Mn(C) more can be said. If E and F are projections, then E ≤ F if and only if im
Image (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
E ⊆ imF. For any two projection, if E ∩ F = V, then the unique projection J with image V and kernel the orthogonal complement of V is the meet of E and F. Since projections form a meet-semilattice
Semilattice
In mathematics, a join-semilattice is a partially ordered set which has a join for any nonempty finite subset. Dually, a meet-semilattice is a partially ordered set which has a meet for any nonempty finite subset...
, the partial isometries on Mn(C) form an inverse semigroup with the product
 .
.* – regular semigroups
A semigroup S with an involution * is called a * – regular semigroup if for every x in S, x* is H-equivalent to some inverse of x, where H is the Green’s relationGreen's relations
In mathematics, Green's relations are five equivalence relations that characterise the elements of a semigroup in terms of the principal ideals they generate. The relations are named for James Alexander Green, who introduced them in a paper of 1951...
H. This defining property can be formulated in several equivalent ways. Another is to say that every L-class contains a projection. An axiomatic definition is the condition that for every x in S there exists an element x’ such that x’xx’ = x’, xx’x = x, ( xx’ )* = xx’, ( x’x )* = x’x. Michael P. Drazin
Michael P. Drazin
Michael P. Drazin is American mathematician, working in noncommutative algebra.-See also:* *-regular semigroup* Drazin inverse-External links:*...
first proved that given x, the element x’ satisfying these axioms is unique. It is called the Moore–Penrose inverse of x. This agrees with the classical definition of the Moore–Penrose inverse of a square matrix.
In the multiplicative
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
semigroup Mn ( C ) of square matrices of order n, the map which assigns a matrix A to its Hermitian conjugate A* is an involution. The semigroup Mn ( C ) is a * – regular semigroup with this involution. The Moore–Penrose inverse of A in this * – regular semigroup is the classical Moore–Penrose inverse of A.
P-systems
An interesting question is to characterize when a regular semigroupRegular semigroup
A regular semigroup is a semigroup S in which every element is regular, i.e., for each element a, there exists an element x such that axa = a. Regular semigroups are one of the most-studied classes of semigroups, and their structure is particularly amenable to study via Green's relations.- Origins...
is a *-regular semigroup. The following characterization was given by M. Yamada. Define a P-system F(S) as subset of the idempotents of S, denoted as usual by E(S). Using the usual notation V(a) for the inverses of a, F(S) needs to satisfy the following axioms:
- For any a in S, there exists a unique a° in V(a) such that aa° and a°a are in F(S)
- For any a in S, and b in F(S), a°ba is in F(S), where ° is the well-defined operation from the previous axiom
- For any a, b in F(S), ab is in E(S); note: not necessarily in F(S)
A regular semigroup S is a *-regular semigroup, as defined by Nordahl & Scheiblich, if and only if it has a p-system F(S). In this case F(S) is the set of projections of S with respect to the operation ° defined by F(S). In an inverse semigroup
Inverse semigroup
In mathematics, an inverse semigroup S is a semigroup in which every element x in S has a unique inversey in S in the sense that x = xyx and y = yxy...
the entire semilattice of idempotents is a p-system. Also, if a regular semigroup S has a p-system that is multiplicatively closed (i.e. subsemigroup), then S is an inverse semigroup. Thus, a p-system may be regarded as a generalization of the semilattice of idempotents of an inverse semigroup.
Free semigroup with involution
Let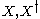 be two disjoint sets in bijective correspondence
be two disjoint sets in bijective correspondenceBijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
given by the map
Map (mathematics)
In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
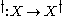 .
.Denote by (here we use
 instead of
instead of  to remind that the union is actually a disjoint union
to remind that the union is actually a disjoint unionDisjoint union
In mathematics, the term disjoint union may refer to one of two different concepts:* In set theory, a disjoint union is a modified union operation that indexes the elements according to which set they originated in; disjoint sets have no element in common.* In probability theory , a disjoint union...
)

and by
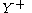 the free semigroup
the free semigroupFree semigroup
In abstract algebra, the free monoid on a set A is the monoid whose elements are all the finite sequences of zero or more elements from A. It is usually denoted A∗. The identity element is the unique sequence of zero elements, often called the empty string and denoted by ε or λ, and the...
on
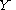 . We can extend the map
. We can extend the mapMap (mathematics)
In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
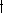 to a map
to a mapMap (mathematics)
In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
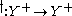
in the following way: given
 for some letters
for some letters 
then we define
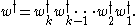
This map
Map (mathematics)
In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
is an involution on the semigroup
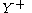 . This is the only way to extend the map
. This is the only way to extend the map 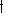 from
from 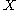 to
to 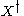 , to an involution on
, to an involution on 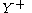 .
.Thus, the semigroup
 with the map
with the map  is a semigroup with involution. Moreover, it is the free semigroup with involution on
is a semigroup with involution. Moreover, it is the free semigroup with involution on 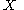 in the sense that it solves the following universal problem
in the sense that it solves the following universal problemUniversal algebra
Universal algebra is the field of mathematics that studies algebraic structures themselves, not examples of algebraic structures....
: given a semigroup with involution
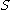 and a map
and a map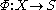 ,
,a semigroup homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
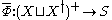
exists such that
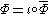
where
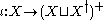
is the inclusion map
Inclusion map
In mathematics, if A is a subset of B, then the inclusion map is the function i that sends each element, x of A to x, treated as an element of B:i: A\rightarrow B, \qquad i=x....
and composition of functions is taken in the diagram order.
It is well known from universal algebra
Universal algebra
Universal algebra is the field of mathematics that studies algebraic structures themselves, not examples of algebraic structures....
that
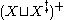 is unique up to isomorphism
is unique up to isomorphismIsomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
s.
If we use
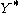 instead of
instead of 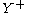 , where
, where
where
 is the empty word (the identity
is the empty word (the identityIdentity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
of the monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
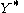 ), we obtain a monoid
), we obtain a monoidMonoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
with involution
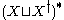 that is the free monoid with involution on
that is the free monoid with involution on 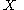 .
.

