
Integration by substitution
Encyclopedia
In calculus
, integration by substitution is a method for finding antiderivative
s and integral
s. Using the fundamental theorem of calculus
often requires finding an antiderivative. For this and other reasons, integration by substitution is an important tool for mathematicians. It is the counterpart to the chain rule
of differentiation
.
Let be an interval and
be an interval and 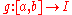 be a continuously differentiable
be a continuously differentiable
function. Suppose that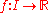 is a continuous function
is a continuous function
. Then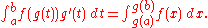
Using Leibniz notation
: the substitution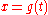 yields
yields  and thus, formally,
and thus, formally, 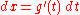 , which is the required substitution for
, which is the required substitution for  . (One could view the method of integration by substitution as a major justification of Leibniz's notation for integrals and derivatives.)
. (One could view the method of integration by substitution as a major justification of Leibniz's notation for integrals and derivatives.)
The formula is used to transform one integral into another integral that is easier to compute. Thus, the formula can be used from left to right or from right to left in order to simplify a given integral. When used in the former manner, it is sometimes known as u-substitution.
as follows. Let ƒ and g be two functions satisfying the above hypothesis that ƒ is continuous on I and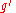 is continuous on the closed interval [a,b]. Then the function
is continuous on the closed interval [a,b]. Then the function  is also continuous on [a,b]. Hence the integrals
is also continuous on [a,b]. Hence the integrals
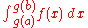
and

in fact exist, and it remains to show that they are equal.
Since ƒ is continuous, it possesses an antiderivative
F. The composite function
 is then defined. Since F and g are differentiable, the chain rule
is then defined. Since F and g are differentiable, the chain rule
gives
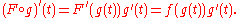
Applying the fundamental theorem of calculus
twice gives
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
, integration by substitution is a method for finding antiderivative
Antiderivative
In calculus, an "anti-derivative", antiderivative, primitive integral or indefinite integralof a function f is a function F whose derivative is equal to f, i.e., F ′ = f...
s and integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
s. Using the fundamental theorem of calculus
Fundamental theorem of calculus
The first part of the theorem, sometimes called the first fundamental theorem of calculus, shows that an indefinite integration can be reversed by a differentiation...
often requires finding an antiderivative. For this and other reasons, integration by substitution is an important tool for mathematicians. It is the counterpart to the chain rule
Chain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
of differentiation
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
.
Let
 be an interval and
be an interval and 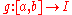 be a continuously differentiable
be a continuously differentiableSmooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
function. Suppose that
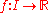 is a continuous function
is a continuous functionContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
. Then
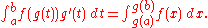
Using Leibniz notation
Leibniz notation
In calculus, Leibniz's notation, named in honor of the 17th-century German philosopher and mathematician Gottfried Wilhelm Leibniz, uses the symbols dx and dy to represent "infinitely small" increments of x and y, just as Δx and Δy represent finite increments of x and y...
: the substitution
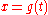 yields
yields  and thus, formally,
and thus, formally, 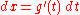 , which is the required substitution for
, which is the required substitution for  . (One could view the method of integration by substitution as a major justification of Leibniz's notation for integrals and derivatives.)
. (One could view the method of integration by substitution as a major justification of Leibniz's notation for integrals and derivatives.)The formula is used to transform one integral into another integral that is easier to compute. Thus, the formula can be used from left to right or from right to left in order to simplify a given integral. When used in the former manner, it is sometimes known as u-substitution.
Relation to the fundamental theorem of calculus
Integration by substitution can be derived from the fundamental theorem of calculusFundamental theorem of calculus
The first part of the theorem, sometimes called the first fundamental theorem of calculus, shows that an indefinite integration can be reversed by a differentiation...
as follows. Let ƒ and g be two functions satisfying the above hypothesis that ƒ is continuous on I and
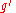 is continuous on the closed interval [a,b]. Then the function
is continuous on the closed interval [a,b]. Then the function  is also continuous on [a,b]. Hence the integrals
is also continuous on [a,b]. Hence the integrals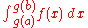
and

in fact exist, and it remains to show that they are equal.
Since ƒ is continuous, it possesses an antiderivative
Antiderivative
In calculus, an "anti-derivative", antiderivative, primitive integral or indefinite integralof a function f is a function F whose derivative is equal to f, i.e., F ′ = f...
F. The composite function
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
 is then defined. Since F and g are differentiable, the chain rule
is then defined. Since F and g are differentiable, the chain ruleChain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
gives
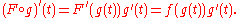
Applying the fundamental theorem of calculus
Fundamental theorem of calculus
The first part of the theorem, sometimes called the first fundamental theorem of calculus, shows that an indefinite integration can be reversed by a differentiation...
twice gives
-
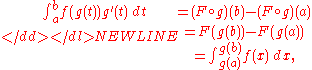
which is the substitution rule.
Examples
Consider the integral
If we make the substitution u = x2 + 1, we obtain du = 2x dx and
-
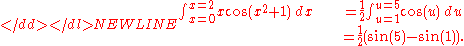
Here we substituted from right to left. It is important to note that since the lower limit x = 0 was replaced with u = 02 + 1 = 1, and the upper limit x = 2 replaced with u = 22 + 1 = 5, a transformation back into terms of x was unnecessary.
For the integral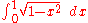
the formula needs to be used from left to right:
the substitution x = sin(u), dx = cos(u) du is useful, because :
:

The resulting integral can be computed using integration by partsIntegration by partsIn calculus, and more generally in mathematical analysis, integration by parts is a rule that transforms the integral of products of functions into other integrals...
or a double angle formula followed by one more substitution. One can also note that the function being integrated is the upper right quarter of a circle with a radius of one, and hence integrating the upper right quarter from zero to one is the geometric equivalent to the area of one quarter of the unit circle, or pi over 4.
Antiderivatives
Substitution can be used to determine antiderivativeAntiderivativeIn calculus, an "anti-derivative", antiderivative, primitive integral or indefinite integralof a function f is a function F whose derivative is equal to f, i.e., F ′ = f...
s. One chooses a relation between x and u, determines the corresponding relation between dx and du by differentiating, and performs the substitutions. An antiderivative for the substituted function can hopefully be determined; the original substitution between u and x is then undone.
Similar to our first example above, we can determine the following antiderivative with this method:
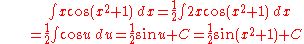
where C is an arbitrary constant of integration.
Note that there were no integral boundaries to transform, but in the last step we had to revert the original substitution u = x2 + 1.
Substitution for multiple variables
One may also use substitution when integrating functions of several variables.
Here the substitution function (v1,...,vn) = φ(u1, ..., un ) needs to be one-to-one and continuously differentiable, and the differentials transform as
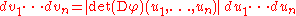
where det(Dφ)(u1, ..., un ) denotes the determinantDeterminantIn linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of the Jacobian matrix containing the partial derivativePartial derivativeIn mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
s of φ . This formula expresses the fact that the absolute valueAbsolute valueIn mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
of the determinant of given vectors equals the volume of the spanned parallelotope.
More precisely, the change of variablesChange of variablesIn mathematics, a change of variables is a basic technique used to simplify problems in which the original variables are replaced with new ones; the new and old variables being related in some specified way...
formula is stated in the next theorem:
Theorem. Let U be an open set in Rn and φ : U → Rn an injectiveInjective functionIn mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
differentiable function with continuous partial derivatives, the Jacobian of which is nonzero for every x in U. Then for any real-valued, compactly supported, continuous function f, with support contained in φ(U),
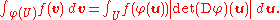
The conditions on the theorem can be weakened in various ways. First, the requirement that φ be continuously differentiable can be replaced by the weaker assumption that φ be merely differentiable and have a continuous inverse . This is guaranteed to hold if φ is continuously differentiable by the inverse function theoremInverse function theoremIn mathematics, specifically differential calculus, the inverse function theorem gives sufficient conditions for a function to be invertible in a neighborhood of a point in its domain...
. Alternatively, the requirement that Det(Dφ)≠0 can be eliminated by applying Sard's theorem .
For Lebesgue measurable functions, the theorem can be stated in the following form :
Theorem. Let U be a measurable subset of Rn and φ : U → Rn an injectiveInjective functionIn mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
function, and suppose for every x in U there exists φ'(x) in Rn,n such that φ(y) = φ(x) + φ'(x) (y − x) + o(||y − x||) as y → x. Then φ(U) is measurable, and for any real-valued function f defined on φ(U),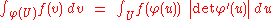
in the sense that if either integral exists (or is properly infinite), then so does the other one, and they have the same value.
Another very general version in measure theory is the following :
Theorem. Let X be a locally compact Hausdorff spaceHausdorff spaceIn topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
equipped with a finite Radon measureRadon measureIn mathematics , a Radon measure, named after Johann Radon, is a measure on the σ-algebra of Borel sets of a Hausdorff topological space X that is locally finite and inner regular.-Motivation:...
μ, and let Y be a σ-compact Hausdorff space with a σ-finite Radon measure ρ. Let φ : X → Y be a continuousContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
and absolutely continuous function (where the latter means that ρ(φ(E)) = 0 whenever μ(E) = 0). Then there exists a real-valued Borel measurable functionBorel algebraIn mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...
w on X such that for every Lebesgue integrable function f : Y → R, the function (f °φ)w is Lebesgue integrable on X, and
Furthermore, it is possible to write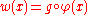
for some Borel measurable function g on Y.
In geometric measure theoryGeometric measure theoryIn mathematics, geometric measure theory is the study of the geometric properties of the measures of sets , including such things as arc lengths and areas. It uses measure theory to generalize differential geometry to surfaces with mild singularities called rectifiable sets...
, integration by substitution is used with Lipschitz functions. A bi-Lipschitz function is a Lipschitz function T : U → Rn which is one-to-one, and such that its inverse function T-1 T(U) → U is also Lipschitz. By Rademacher's theoremRademacher's theoremIn mathematical analysis, Rademacher's theorem, named after Hans Rademacher, states the following: If U is an open subset of Rn andis Lipschitz continuous, then f is Fréchet-differentiable almost everywhere in U In mathematical analysis, Rademacher's theorem, named after Hans Rademacher, states the...
a bi-Lipschitz mapping is differentiable almost everywhereAlmost everywhereIn measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...
. In particular, the Jacobian determinant of a bi-Lipschitz mapping det DT is well-defined almost everywhere. The following result then holds:
Theorem. Let U be an open subset of Rn and T : U → Rn be a bi-Lipschitz mapping. Let f : T(U) → R be measurable. Then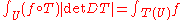
in the sense that if either integral exists (or is properly infinite), then so does the other one, and they have the same value.
The above theorem was first proposed by Euler when he developed the notion of double integrals in 1769. Although generalized to triple integrals by LagrangeLagrangeLa Grange literally means the barn in French. Lagrange may refer to:- People :* Charles Varlet de La Grange , French actor* Georges Lagrange , translator to and writer in Esperanto...
in 1773, and used by LegendreAdrien-Marie LegendreAdrien-Marie Legendre was a French mathematician.The Moon crater Legendre is named after him.- Life :...
, Laplace, GaussGaussGauss may refer to:*Carl Friedrich Gauss, German mathematician and physicist*Gauss , a unit of magnetic flux density or magnetic induction*GAUSS , a software package*Gauss , a crater on the moon...
, and first generalized to n variables by Mikhail Ostrogradski in 1836, it resisted a fully rigorous formal proof for a surprisingly long time, and was first satisfactorily resolved 125 years later, by Élie CartanÉlie CartanÉlie Joseph Cartan was an influential French mathematician, who did fundamental work in the theory of Lie groups and their geometric applications...
in a series of papers beginning in the mid-1890s .
Application in probability
Substitution can be used to answer the following important question in probability: given a random variable with probability density
with probability density  and another random variable
and another random variable  related to
related to  by the equation
by the equation  , what is the probability density for
, what is the probability density for  ?
?
It is easiest to answer this question by first answering a slightly different question: what is the probability that takes a value in some particular subset
takes a value in some particular subset 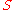 ? Denote this probability
? Denote this probability 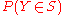 . Of course, if
. Of course, if  has probability density
has probability density 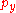 then the answer is
then the answer is

but this isn't really useful because we don't know py; it's what we're trying to find in the first place. We can make progress by considering the problem in the variable .
.  takes a value in S whenever X takes a value in
takes a value in S whenever X takes a value in 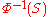 , so
, so
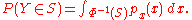
Changing from variable x to y gives

Combining this with our first equation gives
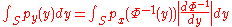
so
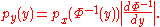
In the case where and
and  depend on several uncorrelated variables, i.e.
depend on several uncorrelated variables, i.e. 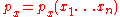 , and
, and  ,
,  can be found by substitution in several variables discussed above. The result is
can be found by substitution in several variables discussed above. The result is
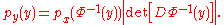
See also
- Substitution of variablesSubstitution of variablesIn mathematics, substitution of variables refers to the substitution of certain variables with other variables....
- Probability density functionProbability density functionIn probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
- Weierstrass substitutionWeierstrass substitutionIn integral calculus, the Weierstrass substitution, named after Karl Weierstrass, is used for finding antiderivatives, and hence definite integrals, of rational functions of trigonometric functions. No generality is lost by taking these to be rational functions of the sine and cosine. The...
- Substitution of variables
-

