Change of variables
Encyclopedia
In mathematics, a change of variables is a basic technique used to simplify problems in which the original variables are replaced with new ones; the new and old variables being related in some specified way. The intent is that the problem expressed in new variables may be simpler, or equivalent to a better understood problem.
A very simple example of a useful variable change can be seen in the problem of finding the roots of the sixth order polynomial:
Sixth order polynomial equations are generally impossible to solve in terms of elementary functions. This particular equation, however, may be simplified by defining a new variable x3 = u. Substituting this into the polynomial:
which is just a quadratic equation
with solutions:
The solution in terms of the original variable is obtained by replacing the original variable:
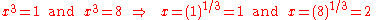
is used to simplify complicated differentiation. For example, to calculate the derivative
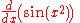
the variable x may be changed by introducing x2 = u. Then, by the chain rule:
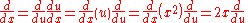
so that
where in the very last step u has been replaced with x2.
and the steps are rarely carried out in full.
The very broad use of variable changes is apparent when considering differential equations, where the independent variables may be changed using the chain rule
or the dependent variables are changed resulting in some differentiation to be carried out. Exotic changes, such as the mingling of dependent and independent variables in point and contact transformations, can be very complicated but allow much freedom.
Very often, a general form for a change is substituted into a problem and parameters picked along the way to best simplify the problem.
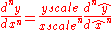
where
This may be shown readily through the chain rule
and linearity of differentiation. This change is very common in practical applications to get physical parameters out of problems, for example, the boundary value problem
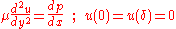
describes parallel fluid flow between flat solid walls separated by a distance δ; µ is the viscosity
and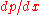
the pressure gradient
, both constants. By scaling the variables the problem becomes
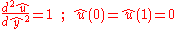
where
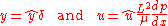
Scaling is useful for many reasons. It simplifies analysis both by reducing the number of parameters and by simply making the problem neater. Proper scaling may normalize variables, that is make them have a sensible unitless range such as 0 to 1. Finally, if a problem mandates numeric solution, the fewer the parameters the fewer the number of computations.
A very simple example of a useful variable change can be seen in the problem of finding the roots of the sixth order polynomial:
Sixth order polynomial equations are generally impossible to solve in terms of elementary functions. This particular equation, however, may be simplified by defining a new variable x3 = u. Substituting this into the polynomial:
which is just a quadratic equation
Quadratic equation
In mathematics, a quadratic equation is a univariate polynomial equation of the second degree. A general quadratic equation can be written in the formax^2+bx+c=0,\,...
with solutions:
The solution in terms of the original variable is obtained by replacing the original variable:
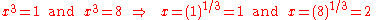
Differentiation
The chain ruleChain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
is used to simplify complicated differentiation. For example, to calculate the derivative
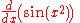
the variable x may be changed by introducing x2 = u. Then, by the chain rule:
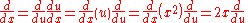
so that
where in the very last step u has been replaced with x2.
Integration
Difficult integrals may often be evaluated by changing variables; this is enabled by the substitution rule and is analogous to the use of the chain rule above.Differential equations
Variable changes for differentiation and integration are taught in elementary calculusCalculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
and the steps are rarely carried out in full.
The very broad use of variable changes is apparent when considering differential equations, where the independent variables may be changed using the chain rule
Chain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
or the dependent variables are changed resulting in some differentiation to be carried out. Exotic changes, such as the mingling of dependent and independent variables in point and contact transformations, can be very complicated but allow much freedom.
Very often, a general form for a change is substituted into a problem and parameters picked along the way to best simplify the problem.
Scaling and shifting
Probably the simplest change is the scaling and shifting of variables, that is replacing them with new variables that are "stretched" and "moved" by constant amounts. This is very common in practical applications to get physical parameters out of problems. For an nth order derivative, the change simply results in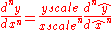where
This may be shown readily through the chain rule
Chain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
and linearity of differentiation. This change is very common in practical applications to get physical parameters out of problems, for example, the boundary value problem
Boundary value problem
In mathematics, in the field of differential equations, a boundary value problem is a differential equation together with a set of additional restraints, called the boundary conditions...
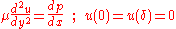
describes parallel fluid flow between flat solid walls separated by a distance δ; µ is the viscosity
Viscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
and
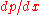the pressure gradientPressure gradient
In atmospheric sciences , the pressure gradient is a physical quantity that describes in which direction and at what rate the pressure changes the most rapidly around a particular location. The pressure gradient is a dimensional quantity expressed in units of pressure per unit length...
, both constants. By scaling the variables the problem becomes
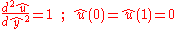
where
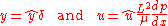
Scaling is useful for many reasons. It simplifies analysis both by reducing the number of parameters and by simply making the problem neater. Proper scaling may normalize variables, that is make them have a sensible unitless range such as 0 to 1. Finally, if a problem mandates numeric solution, the fewer the parameters the fewer the number of computations.