
Substitution of variables
Encyclopedia
In mathematics, substitution of variables (also called variable substitution or coordinate transformation) refers to the substitution of certain variable
s with other variables.
Though the study of how variable substitutions affect a certain problem can be interesting in itself, they are often used when solving mathematical or physical
problems, as the correct substitution may greatly simplify a problem which is hard to solve in the original variables. Under certain conditions the solution to the original problem can be recovered by back-substitution (inverting the substitution).
 ,
,  be smooth manifolds and let
be smooth manifolds and let 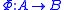 be a
be a 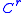 -diffeomorphism
-diffeomorphism
between them, that is: is a
is a  times continuously differentiable, bijective map from
times continuously differentiable, bijective map from  to
to  with
with  times continuously differentiable inverse from
times continuously differentiable inverse from  to
to  . Here
. Here  may be any natural number (or zero),
may be any natural number (or zero),  (smooth
(smooth
) or (analytic
(analytic
).
The map is called a regular coordinate transformation or regular variable substitution, where
is called a regular coordinate transformation or regular variable substitution, where 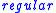 refers to the
refers to the 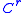 -ness of
-ness of  . Usually one will write
. Usually one will write 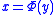 to indicate the replacement of the variable
to indicate the replacement of the variable  by the variable
by the variable  by substituting the value of
by substituting the value of  in
in  for every occurrence of
for every occurrence of  .
.

This may be a potential energy function for some physical problem. If one does not immediately see a solution, one might try the substitution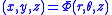 given by
given by 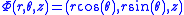 .
.
Note that if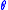 runs outside a
runs outside a  -length interval, for example,
-length interval, for example, 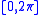 , the map
, the map  is no longer bijective. Therefore
is no longer bijective. Therefore  should be limited to, for example
should be limited to, for example 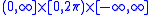 . Notice how
. Notice how  is excluded, for
is excluded, for  is not bijective in the origin (
is not bijective in the origin (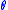 can take any value, the point will be mapped to (0, 0, z)). Then, replacing all occurrences of the original variables by the new expressions prescribed by
can take any value, the point will be mapped to (0, 0, z)). Then, replacing all occurrences of the original variables by the new expressions prescribed by  and using the identity
and using the identity 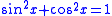 , we get
, we get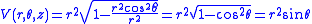 .
.
Now the solutions can be readily found: , so
, so  or
or 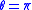 . Applying the inverse of
. Applying the inverse of  shows that this is equivalent to
shows that this is equivalent to  while
while 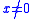 . Indeed we see that for
. Indeed we see that for  the function vanishes, except for the origin.
the function vanishes, except for the origin.
Note that, had we allowed , the origin would also have been a solution, though it is not a solution to the original problem. Here the bijectivity of
, the origin would also have been a solution, though it is not a solution to the original problem. Here the bijectivity of  is crucial.
is crucial.
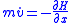
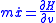
for a given function .
.
The mass can be eliminated by the (trivial) substitution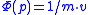 .
.
Clearly this is a bijective map from to
to  . Under the substitution
. Under the substitution 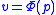 the system becomes
the system becomes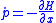
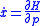
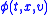 , Newton
, Newton
's equations of motion are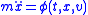 .
.
Lagrange examined how these equations of motion change under an arbitrary substitution of variables ,
,  .
.
He found that the equations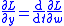
are equivalent to Newton's equations for the function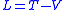 ,
,
where T is the kinetic, and V the potential energy.
In fact, when the substitution is chosen well (exploiting for example symmetries and constraints of the system) these equations are much easier to solve than Newton's equations in Cartesian coordinates.
Variable (mathematics)
In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
s with other variables.
Though the study of how variable substitutions affect a certain problem can be interesting in itself, they are often used when solving mathematical or physical
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
problems, as the correct substitution may greatly simplify a problem which is hard to solve in the original variables. Under certain conditions the solution to the original problem can be recovered by back-substitution (inverting the substitution).
Formal introduction
Let ,
,  be smooth manifolds and let
be smooth manifolds and let 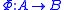 be a
be a 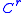 -diffeomorphism
-diffeomorphismDiffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
between them, that is:
 is a
is a  times continuously differentiable, bijective map from
times continuously differentiable, bijective map from  to
to  with
with  times continuously differentiable inverse from
times continuously differentiable inverse from  to
to  . Here
. Here  may be any natural number (or zero),
may be any natural number (or zero),  (smooth
(smoothSmooth
Smooth means having a texture that lacks friction. Not rough.Smooth may also refer to:-In mathematics:* Smooth function, a function that is infinitely differentiable; used in calculus and topology...
) or
 (analytic
(analyticAnalytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
).
The map
 is called a regular coordinate transformation or regular variable substitution, where
is called a regular coordinate transformation or regular variable substitution, where 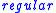 refers to the
refers to the 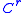 -ness of
-ness of  . Usually one will write
. Usually one will write 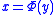 to indicate the replacement of the variable
to indicate the replacement of the variable  by the variable
by the variable  by substituting the value of
by substituting the value of  in
in  for every occurrence of
for every occurrence of  .
.Cylindrical coordinates
Some systems can be more easily solved when switching to cylindrical coordinates. Consider for example the equation
This may be a potential energy function for some physical problem. If one does not immediately see a solution, one might try the substitution
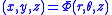 given by
given by 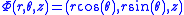 .
.Note that if
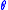 runs outside a
runs outside a  -length interval, for example,
-length interval, for example, 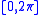 , the map
, the map  is no longer bijective. Therefore
is no longer bijective. Therefore  should be limited to, for example
should be limited to, for example 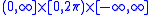 . Notice how
. Notice how  is excluded, for
is excluded, for  is not bijective in the origin (
is not bijective in the origin (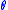 can take any value, the point will be mapped to (0, 0, z)). Then, replacing all occurrences of the original variables by the new expressions prescribed by
can take any value, the point will be mapped to (0, 0, z)). Then, replacing all occurrences of the original variables by the new expressions prescribed by  and using the identity
and using the identity 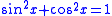 , we get
, we get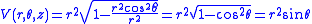 .
.Now the solutions can be readily found:
 , so
, so  or
or 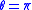 . Applying the inverse of
. Applying the inverse of  shows that this is equivalent to
shows that this is equivalent to  while
while 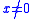 . Indeed we see that for
. Indeed we see that for  the function vanishes, except for the origin.
the function vanishes, except for the origin.Note that, had we allowed
 , the origin would also have been a solution, though it is not a solution to the original problem. Here the bijectivity of
, the origin would also have been a solution, though it is not a solution to the original problem. Here the bijectivity of  is crucial.
is crucial.Integration
Under the proper variable substitution, calculating an integral may become considerably easier. Consult the main article for an example.Momentum vs. velocity
Consider a system of equations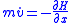
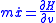
for a given function
 .
.The mass can be eliminated by the (trivial) substitution
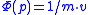 .
.Clearly this is a bijective map from
 to
to  . Under the substitution
. Under the substitution 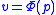 the system becomes
the system becomes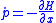
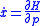
Lagrangian mechanics
Given a force field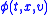 , Newton
, NewtonIsaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
's equations of motion are
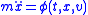 .
.Lagrange examined how these equations of motion change under an arbitrary substitution of variables
 ,
,  .
.He found that the equations
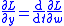
are equivalent to Newton's equations for the function
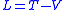 ,
,where T is the kinetic, and V the potential energy.
In fact, when the substitution is chosen well (exploiting for example symmetries and constraints of the system) these equations are much easier to solve than Newton's equations in Cartesian coordinates.
See also
- substitution property of equality
- instantiation of universals

