
Lagrange, Euler and Kovalevskaya tops
Encyclopedia
In classical mechanics, the precession of a top under the influence of gravity is not in general, an integrable problem. There are however three famous cases that are integrable, the Euler, the Lagrange and the Kovalevskaya tops. In addition to the energy, each of these tops involves three additional constants of motion that give rise to the integrability.
The Euler top describes a free top without any particular symmetry, moving in the absence of any external torque. The Lagrange top is a symmetric top, in which the center of gravity lies on the symmetry axis. The Kovalevskaya top is special symmetric top with a unique ratio of the moments of inertia satisfy the relation
 ,
,
and in which the center of gravity is located in the plane perpendicular to the symmetry axis.
 ,
, 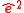 and
and 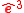 with corresponding moments of inertia
with corresponding moments of inertia 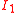 ,
, 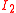 and
and 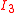 . In a Hamiltonian formulation of classical tops, the conjugate dynamical variables are the components of the angular momentum vector
. In a Hamiltonian formulation of classical tops, the conjugate dynamical variables are the components of the angular momentum vector 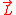 along the principal axes
along the principal axes
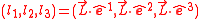
and the z-components of the three principal axes,
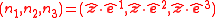
The Poisson algebra of these variables is given by
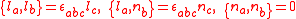
If the position of the center of mass is given by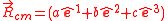 , then the Hamiltonian of a top is given by
, then the Hamiltonian of a top is given by
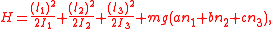
The equations of motion are then determined by

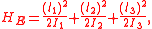
The four constants of motion are the energy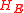 and
and
the three components of angular momentum in the lab frame,
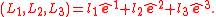
 , with Hamiltonian
, with Hamiltonian
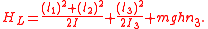
The four constants of motion are the energy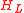 , the angular momentum component along the symmetry axis,
, the angular momentum component along the symmetry axis, 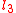 , the angular momentum in the z-direction
, the angular momentum in the z-direction
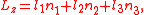
and the magnitude of the n-vector
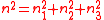
 and the center of mass lies in the plane perpendicular to the symmetry axis
and the center of mass lies in the plane perpendicular to the symmetry axis  . The Hamiltonian is
. The Hamiltonian is
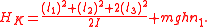
The four constants of motion are the energy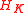 , the Kovalevskaya invariant
, the Kovalevskaya invariant
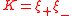
where the variables are defined by
are defined by
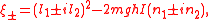
the angular momentum component in the z-direction,

and the magnitude of the n-vector

The Euler top describes a free top without any particular symmetry, moving in the absence of any external torque. The Lagrange top is a symmetric top, in which the center of gravity lies on the symmetry axis. The Kovalevskaya top is special symmetric top with a unique ratio of the moments of inertia satisfy the relation
 ,
,and in which the center of gravity is located in the plane perpendicular to the symmetry axis.
Hamiltonian Formulation of Classical tops
A classical top is defined by three principal axes, defined by the three orthogonal vectors ,
, 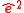 and
and 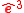 with corresponding moments of inertia
with corresponding moments of inertia 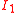 ,
, 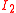 and
and 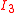 . In a Hamiltonian formulation of classical tops, the conjugate dynamical variables are the components of the angular momentum vector
. In a Hamiltonian formulation of classical tops, the conjugate dynamical variables are the components of the angular momentum vector 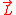 along the principal axes
along the principal axes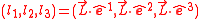
and the z-components of the three principal axes,
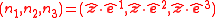
The Poisson algebra of these variables is given by
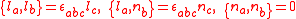
If the position of the center of mass is given by
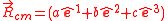 , then the Hamiltonian of a top is given by
, then the Hamiltonian of a top is given by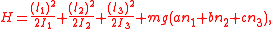
The equations of motion are then determined by

Euler Top
The Euler top is an untorqued top, with Hamiltonian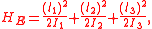
The four constants of motion are the energy
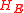 and
andthe three components of angular momentum in the lab frame,
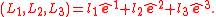
Lagrange Top
The Lagrange top is a symmetric top with the center of mass along the symmetry axis at location, , with Hamiltonian
, with Hamiltonian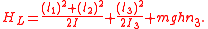
The four constants of motion are the energy
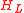 , the angular momentum component along the symmetry axis,
, the angular momentum component along the symmetry axis, 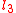 , the angular momentum in the z-direction
, the angular momentum in the z-direction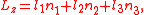
and the magnitude of the n-vector
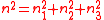
Kovalevskaya Top
The Kovalevskaya top is a symmetric top in which and the center of mass lies in the plane perpendicular to the symmetry axis
and the center of mass lies in the plane perpendicular to the symmetry axis  . The Hamiltonian is
. The Hamiltonian is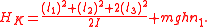
The four constants of motion are the energy
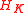 , the Kovalevskaya invariant
, the Kovalevskaya invariant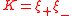
where the variables
 are defined by
are defined by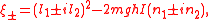
the angular momentum component in the z-direction,

and the magnitude of the n-vector


