
Yang-Baxter equation
Encyclopedia
The Yang–Baxter equation (or star-triangle relation) is an equation which was first introduced in the field of statistical mechanics
. It takes its name from independent work of C. N. Yang from 1968, and R. J. Baxter from 1971. It refers to a principle in integrable systems taking the form of local equivalence transformations which appear in a variety of contexts, such as electric networks, knot theory
and braid groups, and spin
systems, to name just a few.
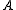 be a unital associative algebra
be a unital associative algebra
. The parameter-dependent Yang–Baxter equation is an equation for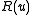 , a parameter-dependent invertible
, a parameter-dependent invertible
element of the tensor product
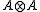 (here,
(here,  is the parameter, which usually ranges over all real numbers in the case of an additive parameter, or over all positive real numbers in the case of a multiplicative parameter). The Yang–Baxter equation is
is the parameter, which usually ranges over all real numbers in the case of an additive parameter, or over all positive real numbers in the case of a multiplicative parameter). The Yang–Baxter equation is
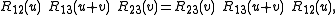
for all values of and
and  , in the case of an additive parameter. At some value of the parameter
, in the case of an additive parameter. At some value of the parameter  can turn into one dimensional projector, this gives rise to quantum determinant. For multiplicative parameter Yang–Baxter equation is
can turn into one dimensional projector, this gives rise to quantum determinant. For multiplicative parameter Yang–Baxter equation is
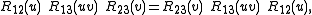
for all values of and
and  , where
, where 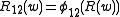 ,
, 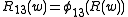 , and
, and 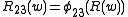 , for all values of the parameter
, for all values of the parameter 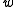 , and
, and 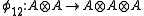 ,
, 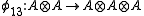 , and
, and 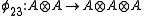 , are algebra morphisms determined by
, are algebra morphisms determined by
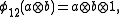
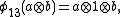
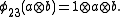
In some cases the determinant of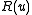 can vanish at specific values of the spectral parameter
can vanish at specific values of the spectral parameter  . Some
. Some 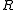 matrices turn into one dimensional projector at
matrices turn into one dimensional projector at
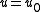 . In this case quantum determinant can be defined.
. In this case quantum determinant can be defined.
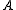 be a unital associative algebra. The parameter-independent Yang–Baxter equation is an equation for
be a unital associative algebra. The parameter-independent Yang–Baxter equation is an equation for  , an invertible element of the tensor product
, an invertible element of the tensor product 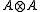 . The Yang–Baxter equation is
. The Yang–Baxter equation is
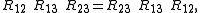
where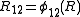 ,
, 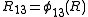 , and
, and 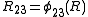 .
.
Let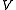 be a module
be a module
of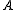 . Let
. Let 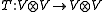 be the linear map satisfying
be the linear map satisfying 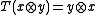 for all
for all 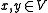 . Then a representation
. Then a representation
of the braid group
,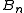 , can be constructed on
, can be constructed on 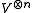 by
by 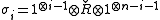 for
for  , where
, where 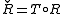 on
on 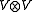 . This representation can be used to determine quasi-invariants of braids
. This representation can be used to determine quasi-invariants of braids
, knots
and links
.
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
. It takes its name from independent work of C. N. Yang from 1968, and R. J. Baxter from 1971. It refers to a principle in integrable systems taking the form of local equivalence transformations which appear in a variety of contexts, such as electric networks, knot theory
Knot theory
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
and braid groups, and spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
systems, to name just a few.
Parameter-dependent Yang–Baxter equation
Let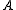 be a unital associative algebra
be a unital associative algebraAlgebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
. The parameter-dependent Yang–Baxter equation is an equation for
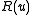 , a parameter-dependent invertible
, a parameter-dependent invertibleInverse element
In abstract algebra, the idea of an inverse element generalises the concept of a negation, in relation to addition, and a reciprocal, in relation to multiplication. The intuition is of an element that can 'undo' the effect of combination with another given element...
element of the tensor product
Tensor product of algebras
In mathematics, the tensor product of two R-algebras is also an R-algebra. This gives us a tensor product of algebras. The special case R = Z gives us a tensor product of rings, since rings may be regarded as Z-algebras....
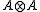 (here,
(here,  is the parameter, which usually ranges over all real numbers in the case of an additive parameter, or over all positive real numbers in the case of a multiplicative parameter). The Yang–Baxter equation is
is the parameter, which usually ranges over all real numbers in the case of an additive parameter, or over all positive real numbers in the case of a multiplicative parameter). The Yang–Baxter equation is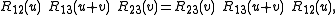
for all values of
 and
and  , in the case of an additive parameter. At some value of the parameter
, in the case of an additive parameter. At some value of the parameter  can turn into one dimensional projector, this gives rise to quantum determinant. For multiplicative parameter Yang–Baxter equation is
can turn into one dimensional projector, this gives rise to quantum determinant. For multiplicative parameter Yang–Baxter equation is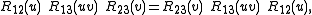
for all values of
 and
and  , where
, where 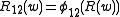 ,
, 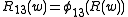 , and
, and 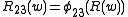 , for all values of the parameter
, for all values of the parameter 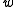 , and
, and 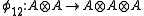 ,
, 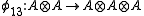 , and
, and 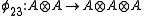 , are algebra morphisms determined by
, are algebra morphisms determined by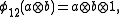
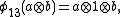
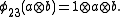
In some cases the determinant of
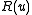 can vanish at specific values of the spectral parameter
can vanish at specific values of the spectral parameter  . Some
. Some 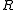 matrices turn into one dimensional projector at
matrices turn into one dimensional projector at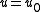 . In this case quantum determinant can be defined.
. In this case quantum determinant can be defined.Parameter-independent Yang–Baxter equation
Let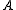 be a unital associative algebra. The parameter-independent Yang–Baxter equation is an equation for
be a unital associative algebra. The parameter-independent Yang–Baxter equation is an equation for  , an invertible element of the tensor product
, an invertible element of the tensor product 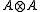 . The Yang–Baxter equation is
. The Yang–Baxter equation is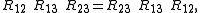
where
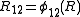 ,
, 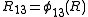 , and
, and 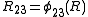 .
.Let
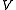 be a module
be a moduleModule (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
of
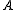 . Let
. Let 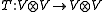 be the linear map satisfying
be the linear map satisfying 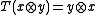 for all
for all 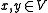 . Then a representation
. Then a representationGroup representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
of the braid group
Braid group
In mathematics, the braid group on n strands, denoted by Bn, is a group which has an intuitive geometrical representation, and in a sense generalizes the symmetric group Sn. Here, n is a natural number; if n > 1, then Bn is an infinite group...
,
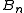 , can be constructed on
, can be constructed on 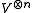 by
by 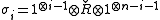 for
for  , where
, where 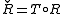 on
on 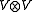 . This representation can be used to determine quasi-invariants of braids
. This representation can be used to determine quasi-invariants of braidsBraid theory
In topology, a branch of mathematics, braid theory is an abstract geometric theory studying the everyday braid concept, and some generalizations. The idea is that braids can be organized into groups, in which the group operation is 'do the first braid on a set of strings, and then follow it with a...
, knots
Knot (mathematics)
In mathematics, a knot is an embedding of a circle in 3-dimensional Euclidean space, R3, considered up to continuous deformations . A crucial difference between the standard mathematical and conventional notions of a knot is that mathematical knots are closed—there are no ends to tie or untie on a...
and links
Link (knot theory)
In mathematics, a link is a collection of knots which do not intersect, but which may be linked together. A knot can be described as a link with one component. Links and knots are studied in a branch of mathematics called knot theory...
.

