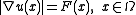Eikonal equation
Encyclopedia
The eikonal equation is a non-linear partial differential equation
encountered in problems of wave propagation
, when the wave equation
is approximated using the WKB theory. It is derivable from Maxwell's equations
of electromagnetics, and provides a link between physical (wave) optics
and geometric (ray) optics.
The eikonal equation is of the form
subject to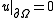
, where 
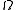is an open set in 
with well-behaved
boundary,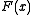
is a function with positive values, 
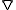denotes the gradient
and |·| is the Euclidean norm. Here, the right-hand side
is typically supplied as known input. Physically, the solution 
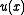is the shortest time needed to travel from the boundary
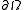to 
inside 
with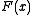 
being the time cost (not speed) at 
.
One fast computational algorithm to approximate the solution to the eikonal equation is the fast marching method
. In the special case when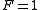
, the solution gives the signed distance from 
.
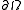where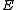
is the electric field intensity and 
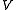is the electric potential. There is a similar equation for velocity potential in fluid flow and temperature in heat transfer. The physical meaning of this equation in the electromagnetic example is that any charge occurring in the region is pushed outward at a right angle from lines of constant potential and this charge travels along lines of constant force given by the field of the E vector. Corresponding variables occur in thermodynamics and fluid flow. Ray optics and electromagnetics are related by the fact that the eikonal equation gives a second electromagnetic formula of the same form as the potential equation above where the line of constant potential has been replaced by a line of constant phase and the force lines have been replaced by normal vectors coming out of the constant phase line at right angles. The magnitude of these normal vectors is given by the square root of the relative permittivity. The line of constant phase can be considered the edge of one of the advancing light waves. The normal vectors are the rays the light is traveling down in ray optics. This explanation is in the RMKS system of units used by electrical engineers.
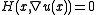
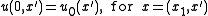
The plane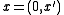
can be thought of as the initial condition, by thinking of 
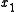as 
We could also solve the equation on a subset of this plane, or on a curved surface, with obvious modifications.
This shows up in geometrical optics
for example, where the equation is
. There it is an equation describing the phase fronts of waves. The lucky thing is that, under reasonable hypothesis on the "initial" data, the eikonal equation admits a local solution. Unfortunately, a global solution (e.g. a solution for all time in the geometrical optics case) is not possible. The reason is that caustics
may develop. In the geometrical optics case, this means that wavefronts cross.
We can solve the eikonal equation using the method of characteristics. Note though that one must make the "non-characteristic" hypothesis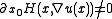
for 
We must also clearly assume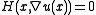 
, for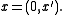 
First, solve the problem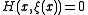
, 
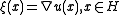. This is done by defining curves (and values of 
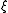on those curves) as
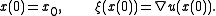Note that even before we have a solution 
, we know 
for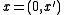 
due to our equation for 
.
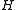That these equations have a solution for some interval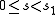
follows from standard ODE theorems (using the non-characteristic hypothesis). These curves fill out an open set
around the plane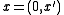
. Thus the curves define the value of 
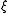in an open set about our initial plane. Once defined as such it is easy to see using the chain rule that 
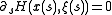, and therefore 
along these curves.
We want our solution
to satisfy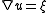 
, or more specifically, for every 
, 
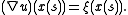Assuming for a minute that this is possible, for any solution 
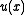we must have
,
and therefore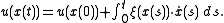
In other words, the solution
will be given in a neighborhood of the initial plane by an explicit equation. However, since the different paths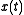 
, starting from different initial points may cross, the solution may become multi-valued, at which point we have developed caustics.
We also have (even before showing that
is a solution)
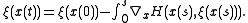
It remains to show that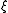
, which we have defined in a neighborhood of our initial plane, is the gradient of some function 
. This will follow if we show that the vector field 
is curl free. Consider the first term in the definition of 
. This term,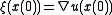 
is curl free as it is the gradient of a function. As for the other term, we note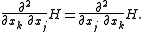
The result follows
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
encountered in problems of wave propagation
Wave propagation
Wave propagation is any of the ways in which waves travel.With respect to the direction of the oscillation relative to the propagation direction, we can distinguish between longitudinal wave and transverse waves....
, when the wave equation
Wave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
is approximated using the WKB theory. It is derivable from Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
of electromagnetics, and provides a link between physical (wave) optics
Physical optics
In physics, physical optics, or wave optics, is the branch of optics which studies interference, diffraction, polarization, and other phenomena for which the ray approximation of geometric optics is not valid...
and geometric (ray) optics.
The eikonal equation is of the form
subject to
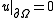, where is an open set in with well-behavedWell-behaved
Mathematicians very frequently speak of whether a mathematical object — a function, a set, a space of one sort or another — is "well-behaved" or not. The term has no fixed formal definition, and is dependent on mathematical interests, fashion, and taste...
boundary,
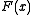is a function with positive values, 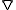denotes the gradientGradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
and |·| is the Euclidean norm. Here, the right-hand side
is typically supplied as known input. Physically, the solution 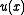is the shortest time needed to travel from the boundaryBoundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
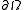to inside with 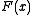being the time cost (not speed) at .One fast computational algorithm to approximate the solution to the eikonal equation is the fast marching method
Fast marching method
The fast marching method is introduced by James A. Sethian as a numerical method for solving boundary value problems of the Eikonal equation:Typically, such a problem describes the evolution of a closed curve as a function of time T with speed F in the normal direction at a point x on the curve...
. In the special case when
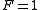, the solution gives the signed distance from 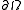.Physical interpretation
The physical meaning of the eikonal equation is related to the formula
where
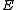is the electric field intensity and 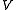is the electric potential. There is a similar equation for velocity potential in fluid flow and temperature in heat transfer. The physical meaning of this equation in the electromagnetic example is that any charge occurring in the region is pushed outward at a right angle from lines of constant potential and this charge travels along lines of constant force given by the field of the E vector. Corresponding variables occur in thermodynamics and fluid flow. Ray optics and electromagnetics are related by the fact that the eikonal equation gives a second electromagnetic formula of the same form as the potential equation above where the line of constant potential has been replaced by a line of constant phase and the force lines have been replaced by normal vectors coming out of the constant phase line at right angles. The magnitude of these normal vectors is given by the square root of the relative permittivity. The line of constant phase can be considered the edge of one of the advancing light waves. The normal vectors are the rays the light is traveling down in ray optics. This explanation is in the RMKS system of units used by electrical engineers.Mathematical description
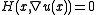
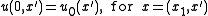
An eikonal equation is one of the formThe plane
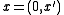can be thought of as the initial condition, by thinking of 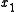as We could also solve the equation on a subset of this plane, or on a curved surface, with obvious modifications.This shows up in geometrical optics
Geometrical optics
Geometrical optics, or ray optics, describes light propagation in terms of "rays". The "ray" in geometric optics is an abstraction, or "instrument", which can be used to approximately model how light will propagate. Light rays are defined to propagate in a rectilinear path as far as they travel in...
for example, where the equation is
. There it is an equation describing the phase fronts of waves. The lucky thing is that, under reasonable hypothesis on the "initial" data, the eikonal equation admits a local solution. Unfortunately, a global solution (e.g. a solution for all time in the geometrical optics case) is not possible. The reason is that causticsCaustic (mathematics)
In differential geometry and geometric optics, a caustic is the envelope of rays either reflected or refracted by a manifold. It is related to the optical concept of caustics...
may develop. In the geometrical optics case, this means that wavefronts cross.
We can solve the eikonal equation using the method of characteristics. Note though that one must make the "non-characteristic" hypothesis
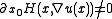for We must also clearly assume 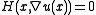, for 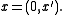First, solve the problem
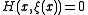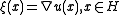, . This is done by defining curves (and values of 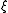on those curves) as 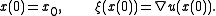Note that even before we have a solution , we know for 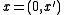due to our equation for 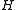.That these equations have a solution for some interval
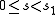follows from standard ODE theorems (using the non-characteristic hypothesis). These curves fill out an open setOpen set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
around the plane
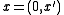. Thus the curves define the value of 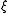in an open set about our initial plane. Once defined as such it is easy to see using the chain rule that 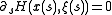, and therefore along these curves.We want our solution
to satisfy 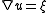, or more specifically, for every , 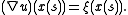Assuming for a minute that this is possible, for any solution 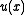we must have,and therefore
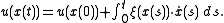
In other words, the solution
will be given in a neighborhood of the initial plane by an explicit equation. However, since the different paths 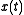, starting from different initial points may cross, the solution may become multi-valued, at which point we have developed caustics.We also have (even before showing that
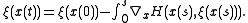
is a solution)It remains to show that
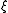, which we have defined in a neighborhood of our initial plane, is the gradient of some function . This will follow if we show that the vector field is curl free. Consider the first term in the definition of . This term, 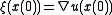is curl free as it is the gradient of a function. As for the other term, we note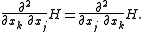The result follows
Applications
- A concrete application is the Computation of radiowave attenuation in the atmosphereComputation of radiowave attenuation in the atmosphereOne of the causes of attenuation of radio propagation is the absorption by the atmosphere. There are many well known facts on the phenomenon and qualitative treatments in textbooks. A document published by the International Telecommunication Union...
. - Finding the Shape from Shading in computer vision.
External links
- The linearized eikonal equation
- The eikonal equation was used for continuum crowd simulation by Treuille, Cooper, and Popović at the University of Washington Animation Research Labs