Generalized dihedral group
Encyclopedia
In mathematics
, the generalized dihedral groups are a family of groups
with algebraic structures similar to that of the dihedral group
s. They include the finite dihedral groups, the infinite dihedral group
, and the orthogonal group
O(2).
H, the generalized dihedral group of H, written Dih(H), is the semidirect product
of H and Z2, with Z2 acting on H by inverting elements. I.e.,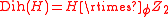
with φ(0) the identity and φ(1) inversion.
Thus we get: * (h2, t2) = (h1 + h2, t2) * (h2, t2) = (h1 − h2, 1 + t2)
for all h1, h2 in H and t2 in Z2.
(Writing Z2 multiplicatively, we have (h1, t1) * (h2, t2) = (h1 + t1h2, t1t2) .)
Note that (h, 0) * (0,1) = (h,1), i.e. first the inversion and then the operation in H. Also (0, 1) * (h, t) = (−h, 1 + t); indeed (0,1) inverts h, and toggles t between "normal" (0) and "inverted" (1) (this combined operation is its own inverse).
The subgroup of Dih(H) of elements (h, 0) is a normal subgroup
of index
2, isomorphic to H, while the elements (h, 1) are all their own inverse.
The conjugacy class
es are:
Thus for every subgroup M of H, the corresponding set of elements (m,0) is also a normal subgroup. We have:
:
etc.
s. Dih(Rn ) consists of two connected
components: the identity component
isomorphic to Rn, and the component with the reflections. Similarly O(2) consists of two connected components: the identity component isomorphic to the circle group, and the component with the reflections.
For the group Dih∞ we can distinguish two cases:
Both topological groups are totally disconnected
, but in the first case the (singleton) components are open, while in the second case they are not. Also, the first topological group is a closed subgroup of Dih(R) but the second is not a closed subgroup of O(2).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the generalized dihedral groups are a family of groups
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
with algebraic structures similar to that of the dihedral group
Dihedral group
In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
s. They include the finite dihedral groups, the infinite dihedral group
Infinite dihedral group
In mathematics, the infinite dihedral group Dih∞ is an infinite group with properties analogous to those of the finite dihedral groups.-Definition:...
, and the orthogonal group
Orthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
O(2).
Definition
For any abelian groupAbelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
H, the generalized dihedral group of H, written Dih(H), is the semidirect product
Semidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
of H and Z2, with Z2 acting on H by inverting elements. I.e.,
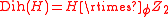with φ(0) the identity and φ(1) inversion.Thus we get: * (h2, t2) = (h1 + h2, t2) * (h2, t2) = (h1 − h2, 1 + t2)
for all h1, h2 in H and t2 in Z2.
(Writing Z2 multiplicatively, we have (h1, t1) * (h2, t2) = (h1 + t1h2, t1t2) .)
Note that (h, 0) * (0,1) = (h,1), i.e. first the inversion and then the operation in H. Also (0, 1) * (h, t) = (−h, 1 + t); indeed (0,1) inverts h, and toggles t between "normal" (0) and "inverted" (1) (this combined operation is its own inverse).
The subgroup of Dih(H) of elements (h, 0) is a normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
of index
Index of a subgroup
In mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
2, isomorphic to H, while the elements (h, 1) are all their own inverse.
The conjugacy class
Conjugacy class
In mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...
es are:
- the sets {(h,0 ), (−h,0 )}
- the sets {(h + k + k, 1) | k in H }
Thus for every subgroup M of H, the corresponding set of elements (m,0) is also a normal subgroup. We have:
-
- Dih(H) / M = Dih ( H / M )
Examples
- Dihn = Dih(Zn) (the dihedral groupDihedral groupIn mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
s)- For even n there are two sets {(h + k + k, 1) | k in H }, and each generates a normal subgroup of type Dihn / 2. As subgroups of the isometry group of the set of vertices of a regular n-gon they are different: the reflections in one subgroup all have two fixed points, while none in the other subgroup has (the rotations of both are the same). However, they are isomorphic as abstract groups.
- For odd n there is only one set {(h + k + k, 1) | k in H }
- Dih∞ = Dih(Z) (the infinite dihedral groupInfinite dihedral groupIn mathematics, the infinite dihedral group Dih∞ is an infinite group with properties analogous to those of the finite dihedral groups.-Definition:...
); there are two sets {(h + k + k, 1) | k in H }, and each generates a normal subgroup of type Dih∞. As subgroups of the isometry group of Z they are different: the reflections in one subgroup all have a fixed point, the mirrors are at the integers, while none in the other subgroup has, the mirrors are in between (the translations of both are the same: by even numbers). However, they are isomorphic as abstract groups. - Dih(S1), or orthogonal groupOrthogonal groupIn mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
O(2,R), or O(2): the isometry group of a circleCircleA circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
, or equivalently, the group of isometries in 2D that keep the origin fixed. The rotations form the circle group S1, or equivalently SO(2,R), also written SO(2), and R/Z ; it is also the multiplicative group of complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s of absolute valueAbsolute valueIn mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
1. In the latter case one of the reflections (generating the others) is complex conjugationComplex conjugateIn mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
. There are no proper normal subgroups with reflections. The discrete normal subgroups are cyclic groups of order n for all positive integers n. The quotient groups are isomorphic with the same group Dih(S1). - Dih(Rn ): the group of isometries of Rn consisting of all translations and inversion in all points; for n = 1 this is the Euclidean groupEuclidean groupIn mathematics, the Euclidean group E, sometimes called ISO or similar, is the symmetry group of n-dimensional Euclidean space...
E(1)Symmetry groups in one dimensionA one-dimensional symmetry group is a mathematical group that describes symmetries in one dimension .A pattern in 1D can be represented as a function f for, say, the color at position x....
; for n > 1 the group Dih(Rn ) is a proper subgroup of E(n ), i.e. it does not contain all isometries. - H can be any subgroup of Rn, e.g. a discrete subgroup; in that case, if it extends in n directions it is a latticeLattice (group)In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...
.- Discrete subgroups of Dih(R2 ) which contain translations in one direction are of frieze groupFrieze groupA frieze group is a mathematical concept to classify designs on two-dimensional surfaces which are repetitive in one direction, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art...
type
and 22
. - Discrete subgroups of Dih(R2 ) which contain translations in two directions are of wallpaper groupWallpaper groupA wallpaper group is a mathematical classification of a two-dimensional repetitive pattern, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art...
type p1 and p2. - Discrete subgroups of Dih(R3 ) which contain translations in three directions are space groupSpace groupIn mathematics and geometry, a space group is a symmetry group, usually for three dimensions, that divides space into discrete repeatable domains.In three dimensions, there are 219 unique types, or counted as 230 if chiral copies are considered distinct...
s of the triclinic crystal systemCrystal systemIn crystallography, the terms crystal system, crystal family, and lattice system each refer to one of several classes of space groups, lattices, point groups, or crystals...
.
- Discrete subgroups of Dih(R2 ) which contain translations in one direction are of frieze group
Properties
Dih(H) is Abelian, with the semidirect product a direct product, if and only if all elements of H are their own inverse, i.e., an elementary abelian 2-groupP-group
In mathematics, given a prime number p, a p-group is a periodic group in which each element has a power of p as its order: each element is of prime power order. That is, for each element g of the group, there exists a nonnegative integer n such that g to the power pn is equal to the identity element...
:
- Dih(Z1) = Dih1 = Z2
- Dih(Z2) = Dih2 = Z2 × Z2 (Klein four-groupKlein four-groupIn mathematics, the Klein four-group is the group Z2 × Z2, the direct product of two copies of the cyclic group of order 2...
) - Dih(Dih2) = Dih2 × Z2 = Z2 × Z2 × Z2
etc.
Topology
Dih(Rn ) and its dihedral subgroups are disconnected topological groupTopological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
s. Dih(Rn ) consists of two connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
components: the identity component
Identity component
In mathematics, the identity component of a topological group G is the connected component G0 of G that contains the identity element of the group...
isomorphic to Rn, and the component with the reflections. Similarly O(2) consists of two connected components: the identity component isomorphic to the circle group, and the component with the reflections.
For the group Dih∞ we can distinguish two cases:
- Dih∞ as the isometry group of Z
- Dih∞ as a 2-dimensional isometry group generated by a rotation by an irrational number of turns, and a reflection
Both topological groups are totally disconnected
Totally disconnected space
In topology and related branches of mathematics, a totally disconnected space is a topological space that is maximally disconnected, in the sense that it has no non-trivial connected subsets...
, but in the first case the (singleton) components are open, while in the second case they are not. Also, the first topological group is a closed subgroup of Dih(R) but the second is not a closed subgroup of O(2).