
Infinite dihedral group
Encyclopedia
In mathematics
, the infinite dihedral group Dih∞ is an infinite group
with properties analogous to those of the finite dihedral group
s.
is a rational multiple of a full rotation, then there is some integer n such that rn is the identity, and we have a finite dihedral group of order 2n. If the rotation is not a rational multiple of a full rotation, then there is no such n and the resulting group has infinitely many elements and is called Dih∞. It has presentations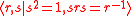

and is isomorphic to a semidirect product
of Z and Z2, and to the free product
Z2 * Z2. It is the automorphism group of the graph consisting of a path infinite to both sides. Correspondingly, it is the isometry group
of Z (see also symmetry groups in one dimension
), the group of all permutations of Z verifying
of Z verifying 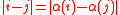 , for each i, j in Z.
, for each i, j in Z.
The infinite dihedral group can also be defined as the holomorph
of the infinite cyclic group.
of real-valued signals; this is realized as follows. If sampling a signal (signal processing
term for a function) at frequency fs, then the functions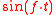 and
and 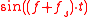 cannot be distinguished (and likewise for
cannot be distinguished (and likewise for  ), which gives the translation (r) element – translation by fs (the detected frequency is periodic). Further, for a real signal,
), which gives the translation (r) element – translation by fs (the detected frequency is periodic). Further, for a real signal,  and
and  so every negative frequency
so every negative frequency
has a corresponding positive frequency (this is not true for complex signals), and gives the reflection (f) element, namely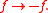 Together these give further reflection symmetries, at fs/2, fs, 1.5fs, etc.; this phenomenon is called folding, as the graph of the detected signal "folds back" on itself, as depicted in the diagram at right.
Together these give further reflection symmetries, at fs/2, fs, 1.5fs, etc.; this phenomenon is called folding, as the graph of the detected signal "folds back" on itself, as depicted in the diagram at right.
Formally, the quotient under aliasing is the orbifold
[0,fs/2], with a Z/2 action at the endpoints (the orbifold points), corresponding to reflection.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the infinite dihedral group Dih∞ is an infinite group
Infinite group
In group theory, an area of mathematics, an infinite group is a group, of which the underlying set contains an infinite number of elements....
with properties analogous to those of the finite dihedral group
Dihedral group
In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
s.
Definition
Every dihedral group is generated by a rotation r and a reflection; if the rotationRotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
is a rational multiple of a full rotation, then there is some integer n such that rn is the identity, and we have a finite dihedral group of order 2n. If the rotation is not a rational multiple of a full rotation, then there is no such n and the resulting group has infinitely many elements and is called Dih∞. It has presentations
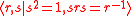

and is isomorphic to a semidirect product
Semidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
of Z and Z2, and to the free product
Free product
In mathematics, specifically group theory, the free product is an operation that takes two groups G and H and constructs a new group G ∗ H. The result contains both G and H as subgroups, is generated by the elements of these subgroups, and is the “most general” group having these properties...
Z2 * Z2. It is the automorphism group of the graph consisting of a path infinite to both sides. Correspondingly, it is the isometry group
Isometry group
In mathematics, the isometry group of a metric space is the set of all isometries from the metric space onto itself, with the function composition as group operation...
of Z (see also symmetry groups in one dimension
Symmetry groups in one dimension
A one-dimensional symmetry group is a mathematical group that describes symmetries in one dimension .A pattern in 1D can be represented as a function f for, say, the color at position x....
), the group of all permutations
 of Z verifying
of Z verifying 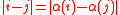 , for each i, j in Z.
, for each i, j in Z.The infinite dihedral group can also be defined as the holomorph
Holomorph (mathematics)
In mathematics, especially in the area of algebra known as group theory, the holomorph of a group is a group which simultaneously contains the group and its automorphism group. The holomorph provides interesting examples of groups, and allows one to treat group elements and group automorphisms in...
of the infinite cyclic group.
Aliasing
A concrete example of infinite dihedral symmetry is in aliasingAliasing
In signal processing and related disciplines, aliasing refers to an effect that causes different signals to become indistinguishable when sampled...
of real-valued signals; this is realized as follows. If sampling a signal (signal processing
Signal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
term for a function) at frequency fs, then the functions
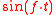 and
and 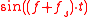 cannot be distinguished (and likewise for
cannot be distinguished (and likewise for  ), which gives the translation (r) element – translation by fs (the detected frequency is periodic). Further, for a real signal,
), which gives the translation (r) element – translation by fs (the detected frequency is periodic). Further, for a real signal,  and
and  so every negative frequency
so every negative frequencyNegative frequency
The concept of negative and positive frequency can be as simple as a wheel rotating one way or the other way. A signed value of frequency indicates both the rate and direction of rotation...
has a corresponding positive frequency (this is not true for complex signals), and gives the reflection (f) element, namely
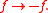 Together these give further reflection symmetries, at fs/2, fs, 1.5fs, etc.; this phenomenon is called folding, as the graph of the detected signal "folds back" on itself, as depicted in the diagram at right.
Together these give further reflection symmetries, at fs/2, fs, 1.5fs, etc.; this phenomenon is called folding, as the graph of the detected signal "folds back" on itself, as depicted in the diagram at right.Formally, the quotient under aliasing is the orbifold
Orbifold
In the mathematical disciplines of topology, geometry, and geometric group theory, an orbifold is a generalization of a manifold...
[0,fs/2], with a Z/2 action at the endpoints (the orbifold points), corresponding to reflection.

