Fermat's principle - AbsoluteAstronomy.com

Optics

Optics is the branch of physics which involves the behavior and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behavior of visible, ultraviolet, and infrared light...

, Fermat
Pierre de Fermat
Pierre de Fermat was a French lawyer at the Parlement of Toulouse, France, and an amateur mathematician who is given credit for early developments that led to infinitesimal calculus, including his adequality...

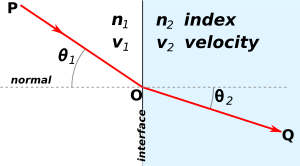
's principle or the principle of least time is the principle that the path taken between two points by a ray

Ray (optics)

In optics, a ray is an idealized narrow beam of light. Rays are used to model the propagation of light through an optical system, by dividing the real light field up into discrete rays that can be computationally propagated through the system by the techniques of ray tracing. This allows even very...

of light is the path that can be traversed in the least time. This principle is sometimes taken as the definition of a ray of light. However, this version of the principle is not general; a more modern statement of the principle is that rays of light traverse the path of stationary optical length.

Fermat's principle can be used to describe the properties of light rays reflected

Reflection (physics)

Reflection is the change in direction of a wavefront at an interface between two differentmedia so that the wavefront returns into the medium from which it originated. Common examples include the reflection of light, sound and water waves...

off mirrors, refracted

Refraction

Refraction is the change in direction of a wave due to a change in its speed. It is essentially a surface phenomenon . The phenomenon is mainly in governance to the law of conservation of energy. The proper explanation would be that due to change of medium, the phase velocity of the wave is changed...

through different media, or undergoing total internal reflection

Total internal reflection

Total internal reflection is an optical phenomenon that happens when a ray of light strikes a medium boundary at an angle larger than a particular critical angle with respect to the normal to the surface. If the refractive index is lower on the other side of the boundary and the incident angle is...

. It follows mathematically from Huygens' principle (at the limit of small wavelength

Wavelength

In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...

), and can be used to derive Snell's law

Snell's law

In optics and physics, Snell's law is a formula used to describe the relationship between the angles of incidence and refraction, when referring to light or other waves passing through a boundary between two different isotropic media, such as water and glass...

of refraction

Refraction

and the law of reflection.

Fermat's principle has the same form as Hamilton's principle

Hamilton's principle

In physics, Hamilton's principle is William Rowan Hamilton's formulation of the principle of stationary action...

and it is the basis of Hamiltonian optics

Hamiltonian optics

Lagrangian optics and Hamiltonian optics are two formulations of geometrical optics which share much of the mathematical formalism with Lagrangian mechanics and Hamiltonian mechanics.-Hamilton's principle:...

. The Hamiltonian formulation of geometrical optics, similar to Winston's formulation, shares much of the mathematical formalism with Hamiltonian mechanics

Hamiltonian mechanics

Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...

Modern version

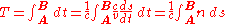
where c is the speed of light

Speed of light

The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...

in vacuum, ds an infinitesimal displacement along the ray, v=ds/dt the speed of light in a medium and n=c/v the refractive index

Refractive index

In optics the refractive index or index of refraction of a substance or medium is a measure of the speed of light in that medium. It is expressed as a ratio of the speed of light in vacuum relative to that in the considered medium....

of that medium. The optical path length of a ray from a point A to a point B is defined by:

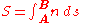
and it is related to the travel time by S=cT. The optical path length is a purely geometrical quantity since time is not considered in its calculation. An extremum in the light travel time between two points A to a point B is equivalent to an extremum of the optical path length between those two points. The historical form proposed by French mathematician Pierre de Fermat

Pierre de Fermat

Pierre de Fermat was a French lawyer at the Parlement of Toulouse, France, and an amateur mathematician who is given credit for early developments that led to infinitesimal calculus, including his adequality...

is incomplete. A complete modern statement of the variational Fermat principle is that In the context of calculus of variations

Calculus of variations

Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...

this can be written as

In general, the refractive index is a scalar field

Scalar field

In mathematics and physics, a scalar field associates a scalar value to every point in a space. The scalar may either be a mathematical number, or a physical quantity. Scalar fields are required to be coordinate-independent, meaning that any two observers using the same units will agree on the...

of position in space, that is,

in 3D

Three-dimensional space

Three-dimensional space is a geometric 3-parameters model of the physical universe in which we live. These three dimensions are commonly called length, width, and depth , although any three directions can be chosen, provided that they do not lie in the same plane.In physics and mathematics, a...

euclidean space

Euclidean space

In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...

. Assuming now that light travels along the x₃ axis, the path of a light ray may be parametrized as

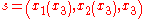and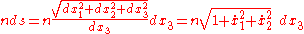

where

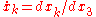. The principle of Fermat can now be written as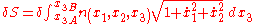

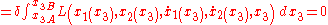
which has the same form as the Hamilton's principle

Hamilton's principle

In physics, Hamilton's principle is William Rowan Hamilton's formulation of the principle of stationary action...

but in which x₃ takes the role of time in classical mechanics

Classical mechanics

In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...

. Function

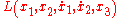is the optical Lagrangian

Lagrangian

The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...

from which the Lagrangian and Hamiltonian (as in Hamiltonian mechanics

Hamiltonian mechanics

) formulations of geometrical optics may be derived.

Derivation

Classically, Fermat's principle can be considered as a mathematical consequence of Huygens' principle. Indeed, of all secondary waves (along all possible paths) the waves with the extrema (stationary) paths contribute most due to constructive interference. Supposing that light waves propagate from A to B by all possible routes AB_j, unrestricted initially by rules of geometrical or physical optics. The various optical paths AB_j will vary by amounts greatly in excess of one wavelength, and so the waves arriving at B will have a large range of phases and will tend to interfere destructively. But if there is a shortest route AB₀, and the optical path varies smoothly through it, then a considerable number of neighboring routes close to AB₀ will have optical paths differing from AB₀ by second-order amounts only and will therefore interfere constructively. Waves along and close to this shortest route will thus dominate and AB₀ will be the route along which the light is seen to travel.

Fermat's principle is the main principle of quantum electrodynamics

Quantum electrodynamics

Quantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved...

where it states that any particle (e.g. a photon or an electron) propagates over all available (unobstructed) paths and the interference (sum, or superposition) of its wavefunction over all those paths (at the point of observer or detector) gives the correct probability of detection of this particle (at this point). Thus the extremal (shortest, longest or stationary) paths contribute into this interference most as they can not be completely canceled out.

In the classic mechanics of waves

WAVES

The WAVES were a World War II-era division of the U.S. Navy that consisted entirely of women. The name of this group is an acronym for "Women Accepted for Volunteer Emergency Service" ; the word "emergency" implied that the acceptance of women was due to the unusual circumstances of the war and...

, Fermat's principle follows from the extremum principle of mechanics (see variational principle

Variational principle

A variational principle is a scientific principle used within the calculus of variations, which develops general methods for finding functions which minimize or maximize the value of quantities that depend upon those functions...

History

Hero of Alexandria

Hero of Alexandria was an ancient Greek mathematician and engineerEnc. Britannica 2007, "Heron of Alexandria" who was active in his native city of Alexandria, Roman Egypt...

(Heron) (c. 60) described a principle of reflection, which stated that a ray of light that goes from point A to point B, suffering any number of reflections on flat mirrors, in the same medium, has a smaller path length than any nearby path.

Ibn al-Haytham (Alhacen), in his Book of Optics
Book of Optics
The Book of Optics ; ; Latin: De Aspectibus or Opticae Thesaurus: Alhazeni Arabis; Italian: Deli Aspecti) is a seven-volume treatise on optics and other fields of study composed by the medieval Muslim scholar Alhazen .-See also:* Science in medieval Islam...

(1021), expanded the principle to both reflection and refraction, and expressed an early version of the principle of least time. His experiments were based on earlier works on refraction carried out by the Greek scientist Ptolemy

Ptolemy

Claudius Ptolemy , was a Roman citizen of Egypt who wrote in Greek. He was a mathematician, astronomer, geographer, astrologer, and poet of a single epigram in the Greek Anthology. He lived in Egypt under Roman rule, and is believed to have been born in the town of Ptolemais Hermiou in the...

The generalized principle of least time in its modern form was stated by Fermat in a letter dated January 1, 1662, to Cureau de la Chambre. It was met with objections made in May 1662 by Claude Clerselier, an expert in optics and leading spokesman for the Cartesians at that time. Amongst his objections, Clerselier states:

... Fermat's principle can not be the cause, for otherwise we would be attributing knowledge to nature: and here, by nature, we understand only that order and lawfulness in the world, such as it is, which acts without foreknowledge, without choice, but by a necessary determination.

The original French, from Mahoney, is as follows:

Le principe que vous prenez pour fondement de votre démonstration, à savoir que la nature agit toujours par les voies les plus courtes et les plus simples, n’est qu’un principe moral et non point physique, qui n’est point et qui ne peut être la cause d’aucun effet de la nature.

Indeed Fermat's principle does not hold standing alone, we now know it can be derived from earlier principles such as Huygens' principle.

Historically, Fermat's principle has served as a guiding principle in the formulation of physical laws with the use of variational calculus (see Principle of least action

Principle of least action

In physics, the principle of least action – or, more accurately, the principle of stationary action – is a variational principle that, when applied to the action of a mechanical system, can be used to obtain the equations of motion for that system...