
Connectedness locus
Encyclopedia
In one-dimensional complex dynamics
, the connectedness
locus
in a parameter space of polynomials or rational functions consists of those parameters for which the corresponding Julia set
is connected.
Without doubt, the most famous connectedness locus is the Mandelbrot set
, which arises from the family
of complex quadratic polynomial
s. The connectedness loci of the higher-degree unicritical families,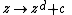
(where ) are often called 'Multibrot set
) are often called 'Multibrot set
s'.
For these families, the bifurcation locus
is the boundary of the connectedness locus. This is no longer true in settings, such as the full parameter space of cubic polynomials, where there is more than one free critical point
. For these families, even maps with disconnected Julia sets may display nontrivial dynamics. Hence here the connectedness locus is generally of less interest.
Complex dynamics
Complex dynamics is the study of dynamical systems defined by iteration of functions on complex number spaces. Complex analytic dynamics is the study of the dynamics of specifically analytic functions.-Techniques:*General** Montel's theorem...
, the connectedness
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
locus
Locus (mathematics)
In geometry, a locus is a collection of points which share a property. For example a circle may be defined as the locus of points in a plane at a fixed distance from a given point....
in a parameter space of polynomials or rational functions consists of those parameters for which the corresponding Julia set
Julia set
In the context of complex dynamics, a topic of mathematics, the Julia set and the Fatou set are two complementary sets defined from a function...
is connected.
Without doubt, the most famous connectedness locus is the Mandelbrot set
Mandelbrot set
The Mandelbrot set is a particular mathematical set of points, whose boundary generates a distinctive and easily recognisable two-dimensional fractal shape...
, which arises from the family

of complex quadratic polynomial
Complex quadratic polynomial
A complex quadratic polynomial is a quadratic polynomial whose coefficients are complex numbers.-Forms:When the quadratic polynomial has only one variable , one can distinguish its 4 main forms:...
s. The connectedness loci of the higher-degree unicritical families,
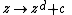
(where
 ) are often called 'Multibrot set
) are often called 'Multibrot setMultibrot set
In mathematics, a multibrot set is the set of values in the complex plane whose absolute value remains below some finite value throughout iterations by a member of the general monic univariate polynomial family of recursions z \mapsto z^d + c . \,...
s'.
For these families, the bifurcation locus
Bifurcation locus
In complex dynamics, the bifurcation locus of a family of holomorphic functions informally is a locus of those maps for which the dynamical behavior changes drastically under a small perturbation of the parameter. Thus the bifurcation locus can be thought of as an analog of the Julia set in...
is the boundary of the connectedness locus. This is no longer true in settings, such as the full parameter space of cubic polynomials, where there is more than one free critical point
Critical point (mathematics)
In calculus, a critical point of a function of a real variable is any value in the domain where either the function is not differentiable or its derivative is 0. The value of the function at a critical point is a critical value of the function...
. For these families, even maps with disconnected Julia sets may display nontrivial dynamics. Hence here the connectedness locus is generally of less interest.

