Axial multipole moments
Encyclopedia
Axial multipole moments are a series expansion
of the electric potential
of a
charge distribution localized close to
the origin
along one
Cartesian axis,
denoted here as the z-axis. However,
the axial multipole expansion can also be applied to
any potential or field that varies inversely
with the distance to the source, i.e., as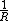
.
For clarity, we first illustrate the expansion for a single point charge,
then generalize to an arbitrary charge density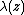
localized to the z-axis.
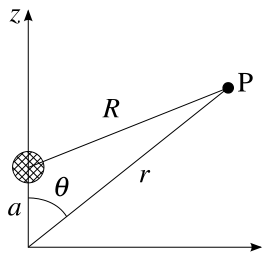
of a point charge q located on
the z-axis at
(Fig. 1) equals
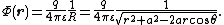
If the radius r of the observation point is greater than a,
we may factor out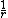
and expand the square root
in powers of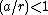
using Legendre polynomials
where the axial multipole moments
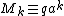contain everything
specific to a given charge distribution; the other parts
of the electric potential
depend only on the coordinates
of the observation point P. Special cases include the axial
monopole
moment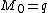
, the axial dipole
moment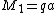
and the axial quadrupole
moment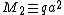
. This
illustrates the general theorem that the lowest
non-zero multipole moment is independent of the
origin
of the coordinate system
,
but higher multipole multipole moments are not (in general).
Conversely, if the radius r is less than a,
we may factor out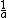
and expand
in powers of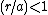
using Legendre polynomials
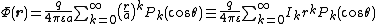
where the interior axial multipole moments
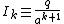contain
everything specific to a given charge distribution;
the other parts depend only on the coordinates of
the observation point P.
point charge of the previous section with an infinitesimal
charge element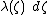
, where
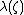represents the charge density at
position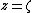
on the z-axis. If the radius r
of the observation point P is greater than the largest
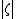for which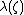 
is significant (denoted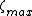
), the electric potential
may be written
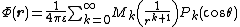
where the axial multipole moments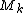
are defined
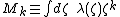
Special cases include the axial monopole
moment (=total charge
)
,
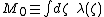the axial dipole
moment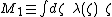
, and
the axial quadrupole
moment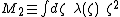
.
Each successive term in the expansion varies inversely with
a greater power of
, e.g., the monopole potential
varies as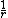
, the dipole potential varies
as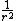
, the quadrupole potential varies
as
, etc. Thus, at large distances
(
), the potential is well-approximated
by the leading nonzero multipole term.
The lowest non-zero axial multipole moment
is invariant under a shift b in
origin
, but higher moments generally
depend on the choice of origin. The shifted multipole moments
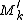would be
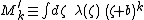
Expanding the polynomial under the integral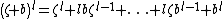
leads to the equation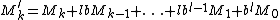
If the lower moments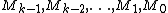
are zero, then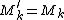
. The same equation shows that multipole moments higher than the first non-zero moment do depend on the choice of origin
(in general).
for which 
is significant (denoted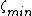
), the electric potential
may be written
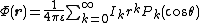
where the interior axial multipole moments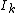
are defined
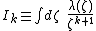
Special cases include the interior axial monopole
moment (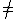
the total charge)
,
the interior axial dipole
moment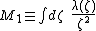
,
etc. Each successive term in the expansion varies with a greater power of
, e.g.,
the interior monopole potential varies as
, the dipole potential varies
as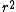
, etc. At short distances (
),
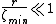the potential is well-approximated by the leading nonzero interior multipole term.
Series expansion
In mathematics, a series expansion is a method for calculating a function that cannot be expressed by just elementary operators . The resulting so-called series often can be limited to a finite number of terms, thus yielding an approximation of the function...
of the electric potential
Electric potential
In classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there...
of a
charge distribution localized close to
the origin
Origin (mathematics)
In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...
along one
Cartesian axis,
denoted here as the z-axis. However,
the axial multipole expansion can also be applied to
any potential or field that varies inversely
with the distance to the source, i.e., as
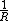.For clarity, we first illustrate the expansion for a single point charge,
then generalize to an arbitrary charge density
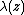
localized to the z-axis.
Axial multipole moments of a point charge
The electric potentialElectric potential
In classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there...
of a point charge q located on
the z-axis at
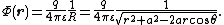
(Fig. 1) equalsIf the radius r of the observation point is greater than a,
we may factor out
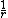and expand the square rootin powers of
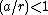using Legendre polynomialswhere the axial multipole moments
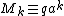contain everythingspecific to a given charge distribution; the other parts
of the electric potential
Electric potential
In classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there...
depend only on the coordinates
of the observation point P. Special cases include the axial
monopole
Monopole
Monopole may refer to:*Magnetic monopole, or Dirac monopole, a hypothetical particle that may be loosely described as a magnet with only one pole, or related concepts in physics and mathematics:...
moment
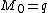, the axial dipoleDipole
In physics, there are several kinds of dipoles:*An electric dipole is a separation of positive and negative charges. The simplest example of this is a pair of electric charges of equal magnitude but opposite sign, separated by some distance. A permanent electric dipole is called an electret.*A...
moment
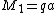and the axial quadrupoleQuadrupole
A quadrupole or quadrapole is one of a sequence of configurations of—for example—electric charge or current, or gravitational mass that can exist in ideal form, but it is usually just part of a multipole expansion of a more complex structure reflecting various orders of complexity.-Mathematical...
moment
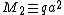. Thisillustrates the general theorem that the lowest
non-zero multipole moment is independent of the
origin
Origin (mathematics)
In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...
of the coordinate system
Coordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
,
but higher multipole multipole moments are not (in general).
Conversely, if the radius r is less than a,
we may factor out
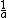and expandin powers of
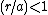using Legendre polynomials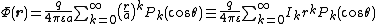where the interior axial multipole moments
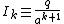containeverything specific to a given charge distribution;
the other parts depend only on the coordinates of
the observation point P.
General axial multipole moments
To get the general axial multipole moments, we replace thepoint charge of the previous section with an infinitesimal
charge element
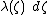, where 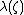represents the charge density atposition
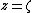on the z-axis. If the radius rof the observation point P is greater than the largest
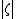for which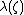 is significant (denoted
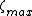), the electric potentialElectric potential
In classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there...
may be written
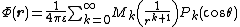
where the axial multipole moments
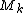are defined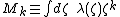Special cases include the axial monopole
Monopole
Monopole may refer to:*Magnetic monopole, or Dirac monopole, a hypothetical particle that may be loosely described as a magnet with only one pole, or related concepts in physics and mathematics:...
moment (=total charge
Electric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
)
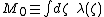,the axial dipole
Dipole
In physics, there are several kinds of dipoles:*An electric dipole is a separation of positive and negative charges. The simplest example of this is a pair of electric charges of equal magnitude but opposite sign, separated by some distance. A permanent electric dipole is called an electret.*A...
moment
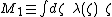, andthe axial quadrupole
Quadrupole
A quadrupole or quadrapole is one of a sequence of configurations of—for example—electric charge or current, or gravitational mass that can exist in ideal form, but it is usually just part of a multipole expansion of a more complex structure reflecting various orders of complexity.-Mathematical...
moment
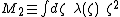.Each successive term in the expansion varies inversely with
a greater power of
, e.g., the monopole potentialvaries as
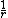, the dipole potential variesas
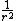, the quadrupole potential variesas
, etc. Thus, at large distances(
), the potential is well-approximatedby the leading nonzero multipole term.
The lowest non-zero axial multipole moment
is invariant under a shift b in
origin
Origin (mathematics)
In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...
, but higher moments generally
depend on the choice of origin. The shifted multipole moments
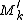would be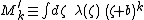Expanding the polynomial under the integral
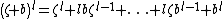
leads to the equation
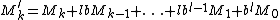
If the lower moments
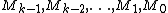
are zero, then
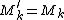. The same equation shows that multipole moments higher than the first non-zero moment do depend on the choice of originOrigin (mathematics)
In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...
(in general).
Interior axial multipole moments
Conversely, if the radius r is smaller than the smallest for which is significant (denoted
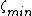), the electric potentialElectric potential
In classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there...
may be written
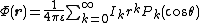
where the interior axial multipole moments
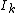are defined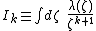Special cases include the interior axial monopole
Monopole
Monopole may refer to:*Magnetic monopole, or Dirac monopole, a hypothetical particle that may be loosely described as a magnet with only one pole, or related concepts in physics and mathematics:...
moment (
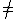the total charge),the interior axial dipole
Dipole
In physics, there are several kinds of dipoles:*An electric dipole is a separation of positive and negative charges. The simplest example of this is a pair of electric charges of equal magnitude but opposite sign, separated by some distance. A permanent electric dipole is called an electret.*A...
moment
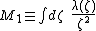,etc. Each successive term in the expansion varies with a greater power of
, e.g.,the interior monopole potential varies as
, the dipole potential variesas
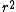, etc. At short distances (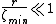),the potential is well-approximated by the leading nonzero interior multipole term.
See also
- Potential theoryPotential theoryIn mathematics and mathematical physics, potential theory may be defined as the study of harmonic functions.- Definition and comments :The term "potential theory" was coined in 19th-century physics, when it was realized that the fundamental forces of nature could be modeled using potentials which...
- Multipole momentsMultipole momentsIn mathematics, especially as applied to physics, multipole moments are the coefficients of a series expansion of a potential due to continuous or discrete sources . A multipole moment usually involves powers of the distance to the origin, as well as some angular dependence...
- Multipole expansionMultipole expansionA multipole expansion is a mathematical series representing a function that depends on angles — usually the two angles on a sphere. These series are useful because they can often be truncated, meaning that only the first few terms need to be retained for a good approximation to the original...
- Legendre polynomials
- Spherical multipole momentsSpherical multipole momentsSpherical multipole moments are the coefficients in a series expansionof a potential that varies inversely with the distance R to a source, i.e., as 1/R...
- Cylindrical multipole momentsCylindrical multipole momentsCylindrical multipole moments are the coefficients in a series expansion of a potential that varies logarithmically with the distance to a source, i.e., as \ln \ R...
- MonopoleMonopoleMonopole may refer to:*Magnetic monopole, or Dirac monopole, a hypothetical particle that may be loosely described as a magnet with only one pole, or related concepts in physics and mathematics:...
- QuadrupoleQuadrupoleA quadrupole or quadrapole is one of a sequence of configurations of—for example—electric charge or current, or gravitational mass that can exist in ideal form, but it is usually just part of a multipole expansion of a more complex structure reflecting various orders of complexity.-Mathematical...
- Solid harmonics
- Laplace expansionLaplace expansion (potential)In physics, the Laplace expansion of a 1/r - type potential is applied to expand Newton's gravitational potential or Coulomb's electrostatic potential. In quantum mechanical calculations on atoms the expansion is used in the evaluation of integrals of the interelectronic repulsion.The Laplace...
- Legendre polynomials