
Solid harmonics
Encyclopedia
In physics
and mathematics
, the solid harmonics are solutions of the Laplace equation in spherical polar coordinates. There are two kinds: the regular solid harmonics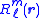 , which vanish at the origin and the irregular solid harmonics
, which vanish at the origin and the irregular solid harmonics  , which are singular at the origin. Both sets of functions play an important role in potential theory
, which are singular at the origin. Both sets of functions play an important role in potential theory
, and are obtained by rescaling spherical harmonics
appropriately:

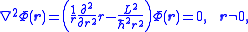
where L2 is the square of the angular momentum operator
,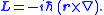
It is known that spherical harmonics
Yml are eigenfunctions of L2,,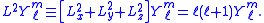
Substitution of Φ(r) = F(r) Yml into the Laplace equation gives, after dividing out the spherical harmonic function, the following radial equation and its general solution,

The particular solutions of the total Laplace equation are regular solid harmonics:
and irregular solid harmonics:
Racah's normalization (also known as Schmidt's semi-normalization) is applied to both functions
(and analogously for the irregular solid harmonic) instead of normalization to unity. This is convenient because in many applications the Racah normalization factor appears unchanged throughout the derivations.

where the Clebsch-Gordan coefficient is given by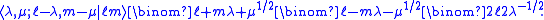
The similar expansion for irregular solid harmonics gives an infinite series,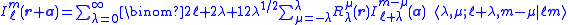
with . The quantity between pointed brackets is again a Clebsch-Gordan coefficient,
. The quantity between pointed brackets is again a Clebsch-Gordan coefficient,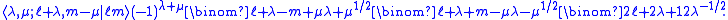
s and real multipole moments
. The explicit cartesian expression of the real regular harmonics will now be derived.

with
where is a Legendre polynomial of order l.
is a Legendre polynomial of order l.
The m dependent phase is known as the Condon-Shortley phase.
The following expression defines the real regular solid harmonics:
and for m = 0:
Since the transformation is by a unitary matrix the normalization of the real and the complex solid harmonics is the same.
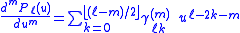
with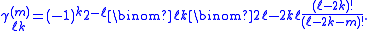
Since z = r cosθ it follows that this derivative, times an appropriate power of r, is a simple polynomial in z,
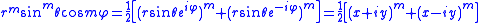
Likewise
Further
and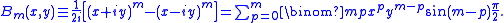

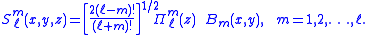
Here
----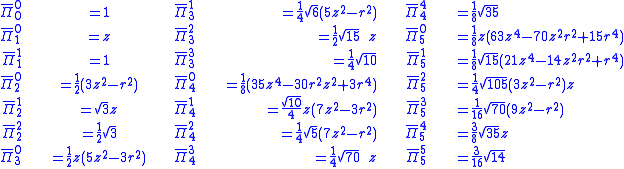
----
The lowest functions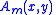 and
and 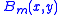 are:
are:
|-
! m
! Am
! Bm
|-
| 0
|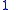
|
|-
| 1
|
|
|-
| 2
|
|
|-
| 3
|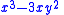
|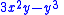
|-
| 4
|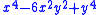
|
|-
| 5
|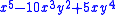
|
|}

One of the 7 components of a real multipole of order 3 (octupole) of a system of N charges qi is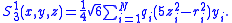

and for m = 0: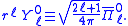
Here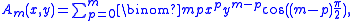
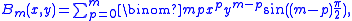
and for m > 0: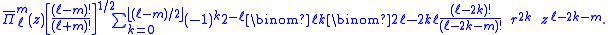
For m = 0:
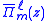 ,
,  , and
, and  listed explicitly above we obtain:
listed explicitly above we obtain: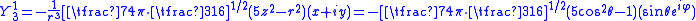
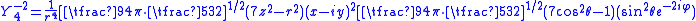
It may be verified that this agrees with the function listed here and here.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
and mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the solid harmonics are solutions of the Laplace equation in spherical polar coordinates. There are two kinds: the regular solid harmonics
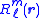 , which vanish at the origin and the irregular solid harmonics
, which vanish at the origin and the irregular solid harmonics  , which are singular at the origin. Both sets of functions play an important role in potential theory
, which are singular at the origin. Both sets of functions play an important role in potential theoryPotential theory
In mathematics and mathematical physics, potential theory may be defined as the study of harmonic functions.- Definition and comments :The term "potential theory" was coined in 19th-century physics, when it was realized that the fundamental forces of nature could be modeled using potentials which...
, and are obtained by rescaling spherical harmonics
Spherical harmonics
In mathematics, spherical harmonics are the angular portion of a set of solutions to Laplace's equation. Represented in a system of spherical coordinates, Laplace's spherical harmonics Y_\ell^m are a specific set of spherical harmonics that forms an orthogonal system, first introduced by Pierre...
appropriately:

Derivation, relation to spherical harmonics
Introducing r, θ, and φ for the spherical polar coordinates of the 3-vector r, we can write the Laplace equation in the following form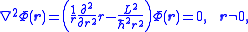
where L2 is the square of the angular momentum operator
Angular momentum operator
In quantum mechanics, the angular momentum operator is an operator analogous to classical angular momentum. The angular momentum operator plays a central role in the theory of atomic physics and other quantum problems involving rotational symmetry...
,
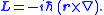
It is known that spherical harmonics
Spherical harmonics
In mathematics, spherical harmonics are the angular portion of a set of solutions to Laplace's equation. Represented in a system of spherical coordinates, Laplace's spherical harmonics Y_\ell^m are a specific set of spherical harmonics that forms an orthogonal system, first introduced by Pierre...
Yml are eigenfunctions of L2,,
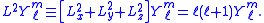
Substitution of Φ(r) = F(r) Yml into the Laplace equation gives, after dividing out the spherical harmonic function, the following radial equation and its general solution,

The particular solutions of the total Laplace equation are regular solid harmonics:

and irregular solid harmonics:

Racah's normalization (also known as Schmidt's semi-normalization) is applied to both functions

(and analogously for the irregular solid harmonic) instead of normalization to unity. This is convenient because in many applications the Racah normalization factor appears unchanged throughout the derivations.
Addition theorems
The translation of the regular solid harmonic gives a finite expansion,
where the Clebsch-Gordan coefficient is given by
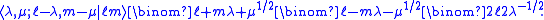
The similar expansion for irregular solid harmonics gives an infinite series,
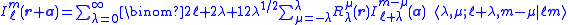
with
 . The quantity between pointed brackets is again a Clebsch-Gordan coefficient,
. The quantity between pointed brackets is again a Clebsch-Gordan coefficient,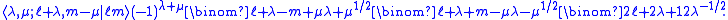
Real form
By a simple linear combination of solid harmonics of ±m these functions are transformed into real functions. The real regular solid harmonics, expressed in cartesian coordinates, are homogeneous polynomials of order l in x, y, z. The explicit form of these polynomials is of some importance. They appear, for example, in the form of spherical atomic orbitalAtomic orbital
An atomic orbital is a mathematical function that describes the wave-like behavior of either one electron or a pair of electrons in an atom. This function can be used to calculate the probability of finding any electron of an atom in any specific region around the atom's nucleus...
s and real multipole moments
Multipole moments
In mathematics, especially as applied to physics, multipole moments are the coefficients of a series expansion of a potential due to continuous or discrete sources . A multipole moment usually involves powers of the distance to the origin, as well as some angular dependence...
. The explicit cartesian expression of the real regular harmonics will now be derived.
Linear combination
We write in agreement with the earlier definition
with

where
 is a Legendre polynomial of order l.
is a Legendre polynomial of order l.The m dependent phase is known as the Condon-Shortley phase.
The following expression defines the real regular solid harmonics:

and for m = 0:

Since the transformation is by a unitary matrix the normalization of the real and the complex solid harmonics is the same.
z-dependent part
Upon writing u = cos θ the mth derivative of the Legendre polynomial can be written as the following expansion in u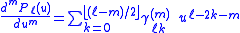
with
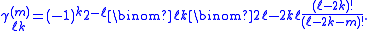
Since z = r cosθ it follows that this derivative, times an appropriate power of r, is a simple polynomial in z,

(x,y)-dependent part
Consider next, recalling that x = r sinθcosφ and y = r sinθsinφ,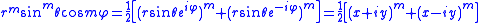
Likewise

Further

and
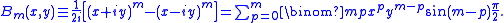
In total

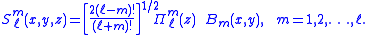
List of lowest functions
We list explicitly the lowest functions up to and including l = 5 .Here

----
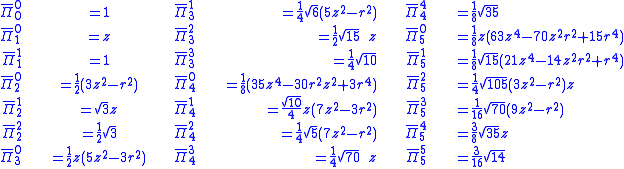
----
The lowest functions
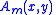 and
and 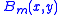 are:
are:-
-
-
- {| class="wikitable"
-
-
|-
! m
! Am
! Bm
|-
| 0
|
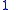
|

|-
| 1
|

|

|-
| 2
|

|

|-
| 3
|
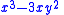
|
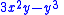
|-
| 4
|
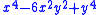
|

|-
| 5
|
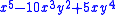
|

|}
Examples
Thus, for example, the angular part of one of the nine normalized spherical g atomic orbitals is:
One of the 7 components of a real multipole of order 3 (octupole) of a system of N charges qi is
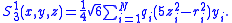
Spherical harmonics in Cartesian form
The following expresses normalized spherical harmonics in Cartesian coordinates (Condon-Shortley phase):
and for m = 0:
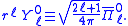
Here
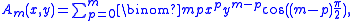
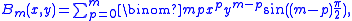
and for m > 0:
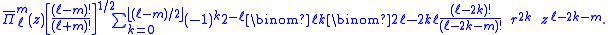
For m = 0:

Examples
Using the expressions for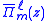 ,
,  , and
, and 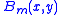 listed explicitly above we obtain:
listed explicitly above we obtain: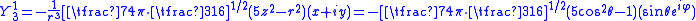
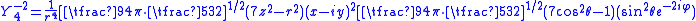
It may be verified that this agrees with the function listed here and here.

