Cylindrical multipole moments
Encyclopedia
Cylindrical multipole moments are the coefficients in a series expansion
of a potential
that varies logarithmically with the distance to a source, i.e., as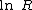
. Such potentials arise in the electric potential
of long line charges, and the analogous sources for the magnetic potential
and gravitational potential.
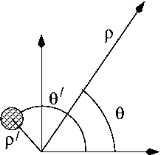
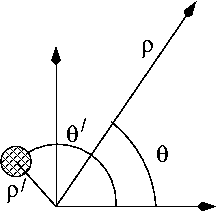
For clarity, we illustrate the expansion for a single line charge, then generalize to an arbitrary distribution of line charges. Through this article, the primed coordinates such
as
refer to the position of the line charge(s), whereas the unprimed coordinates such as 
refer to the point at which the potential is being observed. We use cylindrical coordinates throughout, e.g., an arbitrary vector 
has coordinates 
where
is the radius from the 
axis,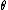 
is the azimuthal angle and 
is the normal Cartesian coordinate. By assumption, the line charges are infinitely long and aligned with the 
axis.
The electric potential
of a line charge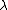
located at 
is given by
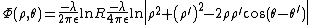
where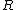
is the shortest distance between the line charge and the observation point.
By symmetry, the electric potential of an infinite linecharge has no
-dependence. The line charge 
is the charge per unit length in the
-direction, and has units of (charge/length). If the radius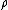 
of the observation point is greater than the radius 
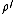of the line charge, we may factor out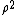 
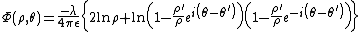
and expand the logarithm
s in powers of
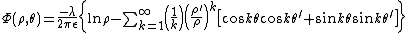
which may be written as
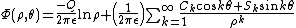
where the multipole moments are defined as
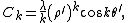
and
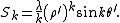
Conversely, if the radius
of the observation point is less than the radius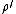 
of the line charge, we may factor out 
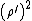and expand the logarithms in powers of 
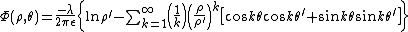
which may be written as
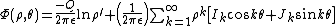
where the interior multipole moments are defined as
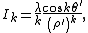
and
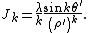
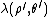is straightforward. The functional form is the same
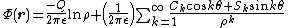
and the moments can be written
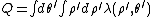
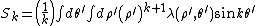
Note that the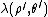
represents the line charge per unit area in the 
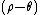plane.
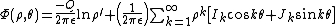
where the moments are defined
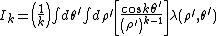
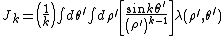
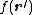be the second charge density, and define 
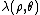as its integral over z
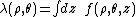
The electrostatic energy is given by the integral of the charge multiplied by the potential due to the cylindrical multipoles
If the cylindrical multipoles are exterior, this equation becomes
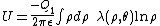
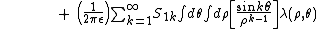
where
, 
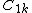and 
are the cylindrical multipole moments of charge distribution 1. This energy formula can be reduced to a remarkably simple form
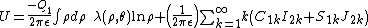
where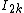
and 
are the interior cylindrical multipoles of the second charge density.
The analogous formula holds if charge density 1 is composed of interior cylindrical multipoles
where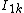
and 
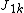are the interior cylindrical multipole moments of charge distribution 1, and 
and 
are the
exterior cylindrical multipoles of the second charge density.
As an example, these formulae could be used to determine the interaction energy of a small protein
in the electrostatic field of a double-stranded DNA
molecule; the latter is relatively straight and bears a constant linear charge density due to the phosphate
groups of its backbone.
Series expansion
In mathematics, a series expansion is a method for calculating a function that cannot be expressed by just elementary operators . The resulting so-called series often can be limited to a finite number of terms, thus yielding an approximation of the function...
of a potential
Potential
*In linguistics, the potential mood*The mathematical study of potentials is known as potential theory; it is the study of harmonic functions on manifolds...
that varies logarithmically with the distance to a source, i.e., as
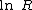. Such potentials arise in the electric potentialElectric potential
In classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there...
of long line charges, and the analogous sources for the magnetic potential
Magnetic potential
The term magnetic potential can be used for either of two quantities in classical electromagnetism: the magnetic vector potential, A, and the magnetic scalar potential, ψ...
and gravitational potential.
For clarity, we illustrate the expansion for a single line charge, then generalize to an arbitrary distribution of line charges. Through this article, the primed coordinates such
as
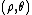refer to the position of the line charge(s), whereas the unprimed coordinates such as refer to the point at which the potential is being observed. We use cylindrical coordinates throughout, e.g., an arbitrary vector has coordinates where
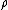is the radius from the axis, 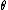is the azimuthal angle and is the normal Cartesian coordinate. By assumption, the line charges are infinitely long and aligned with the axis.Cylindrical multipole moments of a line charge
Electric potential
In classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there...
of a line charge
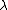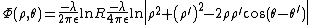
located at is given bywhere
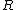is the shortest distance between the line charge and the observation point.By symmetry, the electric potential of an infinite linecharge has no
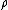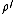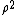
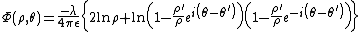
-dependence. The line charge is the charge per unit length in the-direction, and has units of (charge/length). If the radius of the observation point is greater than the radius of the line charge, we may factor out and expand the logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
s in powers of
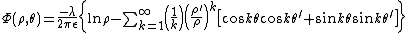
which may be written as
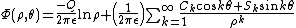
where the multipole moments are defined as
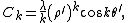
and
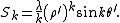
Conversely, if the radius
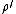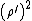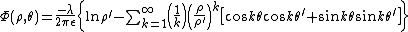
of the observation point is less than the radius of the line charge, we may factor out and expand the logarithms in powers of which may be written as
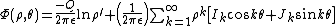
where the interior multipole moments are defined as
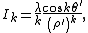
and
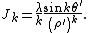
General cylindrical multipole moments
The generalization to an arbitrary distribution of line charges is straightforward. The functional form is the same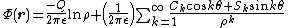and the moments can be written
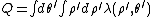
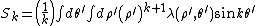
Note that the
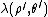represents the line charge per unit area in the 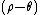plane.Interior cylindrical multipole moments
Similarly, the interior cylindrical multipole expansion has the functional form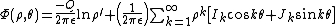where the moments are defined
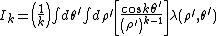
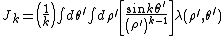
Interaction energies of cylindrical multipoles
A simple formula for the interaction energy of cylindrical multipoles (charge density 1) with a second charge density can be derived. Let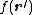 be the second charge density, and define 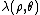as its integral over z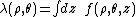The electrostatic energy is given by the integral of the charge multiplied by the potential due to the cylindrical multipoles
If the cylindrical multipoles are exterior, this equation becomes
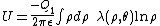
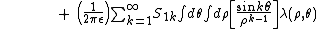
where
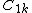, and are the cylindrical multipole moments of charge distribution 1. This energy formula can be reduced to a remarkably simple form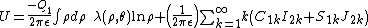where
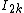and are the interior cylindrical multipoles of the second charge density.The analogous formula holds if charge density 1 is composed of interior cylindrical multipoles
where
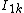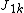and are the interior cylindrical multipole moments of charge distribution 1, and and are theexterior cylindrical multipoles of the second charge density.
As an example, these formulae could be used to determine the interaction energy of a small protein
Protein
Proteins are biochemical compounds consisting of one or more polypeptides typically folded into a globular or fibrous form, facilitating a biological function. A polypeptide is a single linear polymer chain of amino acids bonded together by peptide bonds between the carboxyl and amino groups of...
in the electrostatic field of a double-stranded DNA
DNA
Deoxyribonucleic acid is a nucleic acid that contains the genetic instructions used in the development and functioning of all known living organisms . The DNA segments that carry this genetic information are called genes, but other DNA sequences have structural purposes, or are involved in...
molecule; the latter is relatively straight and bears a constant linear charge density due to the phosphate
Phosphate
A phosphate, an inorganic chemical, is a salt of phosphoric acid. In organic chemistry, a phosphate, or organophosphate, is an ester of phosphoric acid. Organic phosphates are important in biochemistry and biogeochemistry or ecology. Inorganic phosphates are mined to obtain phosphorus for use in...
groups of its backbone.
See also
- Potential theoryPotential theoryIn mathematics and mathematical physics, potential theory may be defined as the study of harmonic functions.- Definition and comments :The term "potential theory" was coined in 19th-century physics, when it was realized that the fundamental forces of nature could be modeled using potentials which...
- Multipole momentsMultipole momentsIn mathematics, especially as applied to physics, multipole moments are the coefficients of a series expansion of a potential due to continuous or discrete sources . A multipole moment usually involves powers of the distance to the origin, as well as some angular dependence...
- Multipole expansionMultipole expansionA multipole expansion is a mathematical series representing a function that depends on angles — usually the two angles on a sphere. These series are useful because they can often be truncated, meaning that only the first few terms need to be retained for a good approximation to the original...
- Axial multipole momentsAxial multipole momentsAxial multipole moments are a series expansionof the electric potential of acharge distribution localized close tothe origin along oneCartesian axis,denoted here as the z-axis...
- Spherical multipole momentsSpherical multipole momentsSpherical multipole moments are the coefficients in a series expansionof a potential that varies inversely with the distance R to a source, i.e., as 1/R...