
Depth of field
Encyclopedia


Optics
Optics is the branch of physics which involves the behavior and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behavior of visible, ultraviolet, and infrared light...
, particularly as it relates to film
Film
A film, also called a movie or motion picture, is a series of still or moving images. It is produced by recording photographic images with cameras, or by creating images using animation techniques or visual effects...
and photography
Photography
Photography is the art, science and practice of creating durable images by recording light or other electromagnetic radiation, either electronically by means of an image sensor or chemically by means of a light-sensitive material such as photographic film...
, depth of field (DOF) is the distance between the nearest and farthest objects in a scene that appear acceptably sharp in an image. Although a lens
Lens (optics)
A lens is an optical device with perfect or approximate axial symmetry which transmits and refracts light, converging or diverging the beam. A simple lens consists of a single optical element...
can precisely focus at only one distance at a time, the decrease in sharpness is gradual on each side of the focused distance, so that within the DOF, the unsharpness is imperceptible under normal viewing conditions.
In some cases, it may be desirable to have the entire image sharp, and a large DOF is appropriate. In other cases, a small DOF may be more effective, emphasizing the subject while de-emphasizing the foreground and background. In cinematography
Cinematography
Cinematography is the making of lighting and camera choices when recording photographic images for cinema. It is closely related to the art of still photography...
, a large DOF is often called deep focus
Deep focus
Deep focus is a photographic and cinematographic technique using a large depth of field. Depth of field is the front-to-back range of focus in an image — that is, how much of it appears sharp and clear. Consequently, in deep focus the foreground, middle-ground and background are all in focus...
, and a small DOF is often called shallow focus
Shallow focus
Shallow focus is a photographic and cinematographic technique incorporating a small depth of field. In shallow focus one plane of the image is in focus while the rest is out of focus. Shallow focus is typically used to emphasize one part of the image over another...
.
The DOF is determined by the camera-to-subject distance, the lens focal length
Focal length
The focal length of an optical system is a measure of how strongly the system converges or diverges light. For an optical system in air, it is the distance over which initially collimated rays are brought to a focus...
, the lens f-number
F-number
In optics, the f-number of an optical system expresses the diameter of the entrance pupil in terms of the focal length of the lens; in simpler terms, the f-number is the focal length divided by the "effective" aperture diameter...
, and the format size
Image sensor format
In digital photography, the image sensor format is the shape and size of the image sensor.The image sensor format of a digital camera determines the angle of view of a particular lens when used with a particular camera...
or circle of confusion
Circle of confusion
In optics, a circle of confusion is an optical spot caused by a cone of light rays from a lens not coming to a perfect focus when imaging a point source...
criterion.
For a given format size, at moderate subject distances, DOF is approximately determined by the subject magnification
Magnification
Magnification is the process of enlarging something only in appearance, not in physical size. This enlargement is quantified by a calculated number also called "magnification"...
and the lens f-number. For a given f-number, increasing the magnification, either by moving closer to the subject or using a lens of greater focal length, decreases the DOF; decreasing magnification increases DOF. For a given subject magnification, increasing the f-number (decreasing the aperture diameter) increases the DOF; decreasing f-number decreases DOF.
When the “same picture” is taken in two different format sizes from the same distance at the same f-number with lenses that give the same angle of view, and the final images (e.g., in prints, or on a projection screen or electronic display) are the same size,
the smaller format has greater DOF.
Many small-format digital SLR camera systems allow using many of the same lenses on both full-frame and “cropped format” cameras. If the subject distance is adjusted to provide the same field of view at the subject, at the same f-number and final-image size, the smaller format has greater DOF, as with the “same picture” comparison above. If pictures are taken from the same distance using the same f-number, and the final images are the same size, the smaller format has less DOF. If pictures taken from the same subject distance are given the same enlargement, both final images will have the same DOF. The final images will, of course, have different sizes.
Cropping an image and enlarging to the same size final image as an uncropped image taken under the same conditions is equivalent to using a smaller format under the same conditions, so the cropped image has less DOF.
When focus is set to the hyperfocal distance
Hyperfocal distance
In optics and photography, hyperfocal distance is a distance beyond which all objects can be brought into an "acceptable" focus. There are two commonly used definitions of hyperfocal distance, leading to values that differ only slightly:...
, the DOF extends from half the hyperfocal distance to infinity, and the DOF is the largest possible for a given f-number.
The advent of digital technology in photography has provided additional means of controlling the extent of image sharpness; some methods allow extended DOF that would be impossible with traditional techniques, and some allow the DOF to be determined after the image is made.
Acceptable sharpness

At any other distance, a point object is defocused, and will produce a blur spot shaped like the aperture
Aperture
In optics, an aperture is a hole or an opening through which light travels. More specifically, the aperture of an optical system is the opening that determines the cone angle of a bundle of rays that come to a focus in the image plane. The aperture determines how collimated the admitted rays are,...
, which for the purpose of analysis is usually assumed to be circular. When this circular spot is sufficiently small, it is indistinguishable from a point, and appears to be in focus; it is rendered as “acceptably sharp”. The diameter of the circle increases with distance from the point of focus; the largest circle that is indistinguishable from a point is known as the acceptable circle of confusion, or informally, simply as the circle of confusion. The acceptable circle of confusion is influenced by visual acuity, viewing conditions, and the amount by which the image is enlarged (Ray 2000, 52–53). The increase of the circle diameter with defocus is gradual, so the limits of depth of field are not hard boundaries between sharp and unsharp.
Several other factors, such as subject matter, movement, and the distance of the subject from the camera, also influence when a given defocus becomes noticeable.
The image format
Film format
A film format is a technical definition of a set of standard characteristics regarding image capture on photographic film, for either stills or movies. It can also apply to projected film, either slides or movies. The primary characteristic of a film format is its size and shape.In the case of...
size affects the depth of field. If the original image is enlarged to make the final image, the circle of confusion in the original image must be smaller than that in the final image by the ratio of enlargement. Moreover, the larger the format size, the longer a lens will need to be to capture the same framing as a smaller format. In motion pictures, for example, a frame with a 12 degree horizontal field of view will require a 50 mm lens on 16 mm film, a 100 mm lens on 35 mm film, and a 250 mm lens on 65 mm film. Conversely, using the same focal length lens with each of these formats will yield a progressively wider image as the film format gets larger: a 50 mm lens has a horizontal field of view of 12 degrees on 16 mm film, 23.6 degrees on 35 mm film, and 55.6 degrees on 65 mm film. What this all means is that because the larger formats require longer lenses than the smaller ones, they will accordingly have a smaller depth of field. Therefore, compensations in exposure, framing, or subject distance need to be made in order to make one format look like it was filmed in another format.
For a 35 mm
35 mm film
35 mm film is the film gauge most commonly used for chemical still photography and motion pictures. The name of the gauge refers to the width of the photographic film, which consists of strips 35 millimeters in width...
motion picture, the image area on the negative is roughly 22 mm by 16 mm (0.87 in by 0.63 in). The limit of tolerable error is usually set at 0.05 mm (0.002 in) diameter. For 16 mm film
16 mm film
16 mm film refers to a popular, economical gauge of film used for motion pictures and non-theatrical film making. 16 mm refers to the width of the film...
, where the image area is smaller, the tolerance is stricter, 0.025 mm (0.001 in). Standard depth-of-field tables are constructed on this basis, although generally 35 mm productions set it at 0.025 mm (0.001 in). Note that the acceptable circle of confusion values for these formats are different because of the relative amount of magnification each format will need in order to be projected on a full-sized movie screen.
(A table for 35 mm still photography would be somewhat different since more of the film is used for each image and the amount of enlargement is usually much less.)
Effect of lens aperture
For a given subject framing and camera position, the DOF is controlled by the lens apertureAperture
In optics, an aperture is a hole or an opening through which light travels. More specifically, the aperture of an optical system is the opening that determines the cone angle of a bundle of rays that come to a focus in the image plane. The aperture determines how collimated the admitted rays are,...
diameter, which is usually specified as the f-number
F-number
In optics, the f-number of an optical system expresses the diameter of the entrance pupil in terms of the focal length of the lens; in simpler terms, the f-number is the focal length divided by the "effective" aperture diameter...
, the ratio of lens focal length
Focal length
The focal length of an optical system is a measure of how strongly the system converges or diverges light. For an optical system in air, it is the distance over which initially collimated rays are brought to a focus...
to aperture diameter. Reducing the aperture diameter (increasing the f-number) increases the DOF; however, it also reduces the amount of light transmitted, and increases diffraction
Diffraction
Diffraction refers to various phenomena which occur when a wave encounters an obstacle. Italian scientist Francesco Maria Grimaldi coined the word "diffraction" and was the first to record accurate observations of the phenomenon in 1665...
, placing a practical limit on the extent to which DOF can be increased by reducing the aperture diameter.
Motion pictures make only limited use of this control; to produce a consistent image quality from shot to shot, cinematographers usually choose a single aperture setting for interiors and another for exteriors, and adjust exposure through the use of camera filters or light levels. Aperture settings are adjusted more frequently in still photography, where variations in depth of field are used to produce a variety of special effects.
Lens DOF scales
Many lenses for small- and medium-format camerasinclude scales that indicate the DOF for a given focus distance and
f-number; the 35 mm lens in the image above is
typical. That lens includes distance scales in feet and meters; when a
marked distance is set opposite the large white index mark, the focus is
set to that distance. The DOF scale below the distance scales includes
markings on either side of the index that correspond to
f-numbers; when the lens is set to a given f-number,
the DOF extends between the distances that align with the
f-number markings.
Zone focusing
When the 35 mm lens above is set to f/11 andfocused at approximately 1.3 m, the DOF (a “zone” of acceptable sharpness)
extends from 1 m to 2 m. Conversely, the required focus and f-number
can be determined from the desired DOF limits by locating the near and far DOF
limits on the lens distance scale and setting focus so that the index mark
is centered between the near and far distance marks; the required
f-number is determined by finding the markings on the DOF scale
that are closest to the near and far distance marks (Ray 1994, 315). For the 35 mm
lens above, if it were desired for the DOF to extend from 1 m to 2 m,
focus would be set so that index mark was centered between the marks for those distances,
and the aperture would be set to f/11.
The focus so determined would be about 1.3 m, the approximate harmonic mean
Harmonic mean
In mathematics, the harmonic mean is one of several kinds of average. Typically, it is appropriate for situations when the average of rates is desired....
of the near and far distances;
see the section Focus and f-number from DOF limits
for additional discussion.
If the marks for the near and far distances fall outside the marks for the largest f-number
on the DOF scale, the desired DOF cannot be obtained; for example, with the 35 mm lens above,
it is not possible to have the DOF extend from 0.7 m to infinity.
The DOF limits can be determined visually, by focusing on the farthest object to be
within the DOF and noting the distance mark on the lens distance scale, and repeating the process
for the nearest object to be within the DOF.
Some distance scales have
markings for only a few distances; for example, the 35 mm lens above
shows only 3 ft and 5 ft on its upper scale. Using other distances
for DOF limits requires visual interpolation between marked distances; because the
distance scale is nonlinear, accurate interpolation can be difficult. In most cases,
English and metric distance markings are not coincident, so using both scales to note
focused distances can sometimes lessen the need for interpolation.
Many autofocus
Autofocus
An autofocus optical system uses a sensor, a control system and a motor to focus fully automatic or on a manually selected point or area. An electronic rangefinder has a display instead of the motor; the adjustment of the optical system has to be done manually until indication...
lenses have smaller distance and DOF scales and fewer
markings than do comparable manual-focus lenses, so that determining focus
and f-number from the scales on an autofocus lens may be more
difficult than with a comparable manual-focus lens. In most cases, determining these settings
using the lens DOF scales on an autofocus lens requires that the lens or camera body be set to manual focus.
On a view camera, the focus and f-number can be obtained by
measuring the focus spread
and performing simple calculations; the procedure is described in more detail in the section
Focus and f-number from DOF limits.
Some view cameras include DOF calculators that indicate focus and f-number without
the need for any calculations by the photographer (Tillmanns 1997, 67–68; Ray 2002, 230–31).
Hyperfocal distance
The hyperfocal distanceHyperfocal distance
In optics and photography, hyperfocal distance is a distance beyond which all objects can be brought into an "acceptable" focus. There are two commonly used definitions of hyperfocal distance, leading to values that differ only slightly:...
is the nearest focus distance at which the DOF extends to infinity; focusing the camera at the hyperfocal distance results in the largest possible depth of field for a given f-number (Ray 2000, 55).
Focusing beyond the hyperfocal distance does not increase the far DOF (which already extends to infinity), but it does decrease the DOF in front of the subject, decreasing the total DOF. Some photographers consider this wasting DOF; however, see Object field methods below for a rationale for doing so.
If the lens includes a DOF scale, the hyperfocal distance can be set by aligning the infinity mark on the distance scale with the mark on the DOF scale corresponding to the f-number to which the lens is set. For example, with the 35 mm lens shown above set to f/11, aligning the infinity mark with the ‘11’ to the left of the index mark on the DOF scale would set the focus to the hyperfocal distance.
Focusing on the hyperfocal distance is a special case of zone focusing in which the far limit of DOF is at infinity.
Object field methods
Traditional depth-of-field formulas and tables assume equal circles ofconfusion for near and far objects. Some authors, such as
Merklinger (1992),
have suggested that distant objects often need to be much sharper to be
clearly recognizable, whereas closer objects, being larger on the film, do
not need to be so sharp. The loss of detail in distant objects may be
particularly noticeable with extreme enlargements. Achieving this additional
sharpness in distant objects usually requires focusing beyond the
hyperfocal distance, sometimes almost at infinity. For example, if
photographing a cityscape with a traffic bollard in the foreground, this
approach, termed the object field method by Merklinger, would recommend
focusing very close to infinity, and stopping down to make the bollard
sharp enough. With this approach, foreground objects cannot always be made
perfectly sharp, but the loss of sharpness in near objects may be
acceptable if recognizability of distant objects is paramount.
Other authors (Adams 1980, 51) have taken the opposite position, maintaining that slight unsharpness in foreground objects is usually more disturbing than slight unsharpness in distant parts of a scene.
Moritz von Rohr
Moritz von Rohr
Moritz von Rohr was an optical scientist at Carl Zeiss in Jena.A street in Jena is named after him: Moritz-von-Rohr-Straße, near Carl-Zeiss-Promenade and Otto-Schott-Straße, reminders of the proud optical heritage of the city.-Life:...
also used an object field method, but unlike Merklinger, he
used the conventional criterion of a maximum circle of confusion diameter in
the image plane, leading to unequal front and rear depths of field.
Limited DOF: selective focus



In some cases, such as landscapes, it may be desirable to have the entire image sharp,
and a large DOF is appropriate. In other cases, artistic considerations may dictate that only
a part of the image be in focus, emphasizing the subject while de-emphasizing the background,
perhaps giving only a suggestion of the environment (Langford 1973, 81).
For example, a common technique in melodrama
Melodrama
The term melodrama refers to a dramatic work that exaggerates plot and characters in order to appeal to the emotions. It may also refer to the genre which includes such works, or to language, behavior, or events which resemble them...
s and horror film
Horror film
Horror films seek to elicit a negative emotional reaction from viewers by playing on the audience's most primal fears. They often feature scenes that startle the viewer through the means of macabre and the supernatural, thus frequently overlapping with the fantasy and science fiction genres...
s is a closeup of a person's face,
with someone just behind that person visible but out of focus. A portrait
Portrait
thumb|250px|right|Portrait of [[Thomas Jefferson]] by [[Rembrandt Peale]], 1805. [[New-York Historical Society]].A portrait is a painting, photograph, sculpture, or other artistic representation of a person, in which the face and its expression is predominant. The intent is to display the likeness,...
or
close-up
Macro photography
Macrophotography is close-up photography, usually of very small subjects. Classically a macrophotograph is one in which the size of the subject on the negative is greater than life size. However in modern use it refers to a finished photograph of a subject at greater than life size...
still photograph might use a small DOF to isolate the subject
from a distracting background. The use of limited DOF to emphasize one part of an image is known
as selective focus, differential focus or shallow focus
Shallow focus
Shallow focus is a photographic and cinematographic technique incorporating a small depth of field. In shallow focus one plane of the image is in focus while the rest is out of focus. Shallow focus is typically used to emphasize one part of the image over another...
.
Although a small DOF implies that other parts of the image will be unsharp, it does not, by itself, determine how unsharp those parts will be. The amount of background (or foreground) blur depends on the distance from the plane of focus, so if a background is close to the subject, it may be difficult to blur sufficiently even with a small DOF. In practice, the lens f-number is usually adjusted until the background or foreground is acceptably blurred, often without direct concern for the DOF.
Sometimes, however, it is desirable to have the entire subject sharp while ensuring that the background is sufficiently unsharp. When the distance between subject and background is fixed, as is the case with many scenes, the DOF and the amount of background blur are not independent. Although it is not always possible to achieve both the desired subject sharpness and the desired background unsharpness, several techniques can be used to increase the separation of subject and background.
For a given scene and subject magnification, the background blur increases with lens focal length. If it is not important that background objects be unrecognizable, background de-emphasis can be increased by using a lens of longer focal length and increasing the subject distance to maintain the same magnification. This technique requires that sufficient space in front of the subject be available; moreover, the perspective of the scene changes because of the different camera position, and this may or may not be acceptable.
The situation is not as simple if it is important that a background object, such as a sign, be unrecognizable. The magnification of background objects also increases with focal length, so with the technique just described, there is little change in the recognizability of background objects.
However, a lens of longer focal length may still be of some help; because of the narrower angle of view, a slight change of camera position may suffice to eliminate the distracting object from the field of view.
Although tilt and swing are normally used to maximize the part of the image that is within the DOF, they also can be used, in combination with a small f-number, to give selective focus to a plane that isn't perpendicular to the lens axis. With this technique, it is possible to have objects at greatly different distances from the camera in sharp focus and yet have a very shallow DOF. The effect can be interesting because it differs from what most viewers are accustomed to seeing.
Near:far distribution
The DOF beyond the subject is always greater than the DOF in front of the subject. When the subject is at the hyperfocal distance or beyond, the far DOF is infinite, so the ratio is 1:∞; as the subject distance decreases, near:far DOF ratio increases, approaching unity at high magnification. For large apertures at typical portrait distances, the ratio is still close to 1:1. The oft-cited rule that 1/3 of the DOF is in front of the subject and 2/3 is beyond (a 1:2 ratio) is true only when the subject distance is 1/3 the hyperfocal distance.DOF vs. format size
The comparative DOFs of two different format sizes depend on the conditions of the comparison;the DOF for the smaller format can be either more than or less than that for the larger format. In the discussion that follows, it is assumed that the final images from both formats are the same size, are viewed from the same distance, and are judged with the same circle of confusion
Circle of confusion
In optics, a circle of confusion is an optical spot caused by a cone of light rays from a lens not coming to a perfect focus when imaging a point source...
criterion.
Derivations of the effects of format size are given under
Derivation of the DOF formulas.
“Same picture” for both formats
For the common “same picture” comparison, i.e., the same camera position and angle of view,
DOF is, to a first approximation, inversely proportional to format size
(Stroebel 1976, 139).
More precisely, if photographs with the same final-image size are taken in
two different camera formats at the same subject distance with the same
angle of view and f-number, the DOF is, to a first
approximation, inversely proportional to the format size. Though commonly used
when comparing formats, the approximation is valid only when the subject
distance is large in comparison with the focal length of the larger format
and small in comparison with the hyperfocal distance of the smaller format.
To maintain the same angle of view, the lens focal lengths must be in
proportion to the format sizes. Assuming, for purposes of comparison, that
the 4×5 format is four times the size of 35 mm format, if a
4×5 camera used a 300 mm lens, a 35 mm camera would need a
75 mm lens for the same field of view. For the same
f-number, the image made with the 35 mm camera would have
four times the DOF of the image made with the 4×5 camera.
Same focal length for both formats
Many small-format digital SLR camera systems allow using many of the same lenses
on both full-frame and “cropped format” cameras.
If the subject distance is adjusted to provide the same field of view at the subject,
at the same f-number and final-image size, the smaller format has more DOF, as
with the “same picture” comparison above. But the pictures
from the two formats will differ because of the different angles of view and the different
viewpoints.
If pictures are taken from the same distance
using the same lens and f-number, and the final images are the same size,
the original image (that recorded on the film or electronic sensor) from the smaller format
requires greater enlargement for the same size
final image, and the smaller format has less DOF. The pictures
from the two formats will differ because of the different angles of view. If the larger format is cropped to the captured area of the smaller format, the final images will have the same angle of view, have been given the same enlargement, and have the same DOF.
Cropping
Cropping an image and enlarging to the same size final image as an uncropped image
taken under the same conditions with a smaller format is equivalent to using the smaller format;
the cropped image has less DOF than the original image from the larger format (Stroebel 1976, 134, 136–37).
Same DOF for both formats
In many cases, the DOF is fixed by the requirements of the desired image.
For a given DOF and field of view, the required f-number is
proportional to the format size. For example, if a 35 mm camera
required 11, a 4×5 camera would require 45 to give the
same DOF. For the same ISO speed, the exposure time on the 4×5 would
be sixteen times as long; if the 35 camera required 1/250 second, the
4×5 camera would require 1/15 second. The longer
exposure time with the larger camera might result in motion blur
Motion blur
Motion blur is the apparent streaking of rapidly moving objects in a still image or a sequence of images such as a movie or animation. It results when the image being recorded changes during the recording of a single frame, either due to rapid movement or long exposure.- Photography :When a camera...
,
especially with windy conditions, a moving subject, or an unsteady camera.
Adjusting the f-number to the camera format is equivalent to
maintaining the same absolute aperture diameter; when set to the same absolute
aperture diameters, both formats have the same DOF.
Advantages and disadvantages of greater DOF
The greater DOF with the smaller format when taking the “same picture” can be either an advantage or a
disadvantage, depending on the desired effect. For the same amount of
foreground and background blur, a small-format camera requires a smaller
f-number and allows a shorter exposure time than a large-format
camera; however, many point-and-shoot digital cameras cannot provide a very shallow
DOF. For example, a point-and-shoot digital camera with a 1/1.8″
sensor (7.18 mm × 5.32 mm) at a normal focal
length and 2.8 has the same DOF as a 35 mm camera with a normal
lens at 13.
Camera movements and DOF
When the lens axis is perpendicular to the image planeFilm plane
A film plane is the area inside any image taking device with a lens and a digital sensor or film; such as a camera. The film plane varies in distance from the lens focal point in each manufacturer...
, as is normally the
case, the plane of focus (POF) is parallel to the image plane, and the DOF
extends between parallel planes on either side of the POF. When the lens
axis is not perpendicular to the image plane, the POF is no longer parallel
to the image plane; the ability to rotate the POF is
known as the Scheimpflug principle
Scheimpflug principle
The Scheimpflug principle is a geometric rule that describes the orientation of the plane of focus of an optical system when the lens plane is not parallel to the image plane. It is commonly applied to the use of camera movements on a view camera...
. Rotation of the POF is
accomplished with camera movements
(tilt, a rotation of the lens about a horizontal axis, or swing, a rotation
about a vertical axis). Tilt and swing are available on most view camera
View camera
The view camera is a type of camera first developed in the era of the Daguerreotype and still in use today, though with many refinements. It comprises a flexible bellows which forms a light-tight seal between two adjustable standards, one of which holds a lens, and the other a viewfinder or a...
s, and
are also available with specific lenses on some small- and medium-format
cameras.
When the POF is rotated, the near and far limits of DOF are no longer
parallel; the DOF becomes wedge-shaped, with the apex of the wedge nearest
the camera (Merklinger 1993, 31–32; Tillmanns 1997, 71). With tilt,
the height of the DOF increases with distance
from the camera; with swing, the width of the DOF increases with distance.
In some cases, rotating the POF can better fit the DOF to the
scene, and achieve the required sharpness at a smaller f-number.
Alternatively, rotating the POF, in combination with a small f-number,
can minimize
Tilted plane focus
"Tilted plane photography" is a method of employing focus as a descriptive, narrative or symbolic artistic device. It is distinct from the more simple uses of selective focus which highlight or emphasise a single point in an image, create an atmospheric bokeh, or miniaturise an obliquely-viewed...
the part of an image that is within the DOF.
DOF formulas
The basis of these formulas is given in the sectionDerivation of the DOF formulas;
refer to the diagram in that section for illustration of the quantities discussed below.
Hyperfocal Distance
Let be the lens focal length
be the lens focal lengthFocal length
The focal length of an optical system is a measure of how strongly the system converges or diverges light. For an optical system in air, it is the distance over which initially collimated rays are brought to a focus...
,
 be the lens f-number
be the lens f-numberF-number
In optics, the f-number of an optical system expresses the diameter of the entrance pupil in terms of the focal length of the lens; in simpler terms, the f-number is the focal length divided by the "effective" aperture diameter...
, and
 be the
be thecircle of confusion
Circle of confusion
In optics, a circle of confusion is an optical spot caused by a cone of light rays from a lens not coming to a perfect focus when imaging a point source...
for a given image format
Film format
A film format is a technical definition of a set of standard characteristics regarding image capture on photographic film, for either stills or movies. It can also apply to projected film, either slides or movies. The primary characteristic of a film format is its size and shape.In the case of...
. The
hyperfocal distance
 is given by
is given by
Moderate-to-large distances
Let be the distance at which the camera is focused (the
be the distance at which the camera is focused (the“subject distance”). When
 is large in comparison with the
is large in comparison with thelens focal length
Focal length
The focal length of an optical system is a measure of how strongly the system converges or diverges light. For an optical system in air, it is the distance over which initially collimated rays are brought to a focus...
, the distance
 from the
from thecamera to the near limit of DOF and the distance

from the camera to the far limit of DOF are

and

The depth of field
 is
is
Substituting for
 and rearranging, DOF can be expressed as
and rearranging, DOF can be expressed as
Thus, for a given image format
Film format
A film format is a technical definition of a set of standard characteristics regarding image capture on photographic film, for either stills or movies. It can also apply to projected film, either slides or movies. The primary characteristic of a film format is its size and shape.In the case of...
, depth of field is determined
by three factors: the focal length
Focal length
The focal length of an optical system is a measure of how strongly the system converges or diverges light. For an optical system in air, it is the distance over which initially collimated rays are brought to a focus...
of the lens, the f-number of the
lens opening (the aperture
Aperture
In optics, an aperture is a hole or an opening through which light travels. More specifically, the aperture of an optical system is the opening that determines the cone angle of a bundle of rays that come to a focus in the image plane. The aperture determines how collimated the admitted rays are,...
), and the camera-to-subject distance.
When the subject distance is the hyperfocal distance,

and

For
 , the far limit of DOF is at infinity and the DOF
, the far limit of DOF is at infinity and the DOFis infinite; of course, only objects at or beyond the near limit of DOF
will be recorded with acceptable sharpness.
Close-up

 approaches the focal length, using
approaches the focal length, usingthe formulas given above can result in significant errors. For close-up
work, the hyperfocal distance has little applicability, and it usually is
more convenient to express DOF in terms of image magnification. Let
 be the magnification; when the subject distance is small in
be the magnification; when the subject distance is small incomparison with the hyperfocal distance,

so that for a given magnification, DOF is independent of focal length.
Stated otherwise, for the same subject magnification, at the same f-number, all focal lengths
used on a given image format
Film format
A film format is a technical definition of a set of standard characteristics regarding image capture on photographic film, for either stills or movies. It can also apply to projected film, either slides or movies. The primary characteristic of a film format is its size and shape.In the case of...
give approximately the same DOF. This statement is true only when
the subject distance is small in comparison with the hyperfocal distance,
however.
The discussion thus far has assumed a symmetrical lens for which the
entrance and exit pupils coincide with the front and rear
nodal planes, and for which the pupil magnification
Pupil magnification
The pupil magnification of an optical system is the ratio of the diameter of the exit pupil to the diameter of the entrance pupil. The pupil magnification is used in calculations of the effective f-number, which affects a number of important elements related to optics, such as exposure,...
(the ratio of exit pupil
Exit pupil
In optics, the exit pupil is a virtual aperture in an optical system. Only rays which pass through this virtual aperture can exit the system. The exit pupil is the image of the aperture stop in the optics that follow it. In a telescope or compound microscope, this image is the image of the...
diameter to that of the
entrance pupil
Entrance pupil
In an optical system, the entrance pupil is the optical image of the physical aperture stop, as 'seen' through the front of the lens system. The corresponding image of the aperture as seen through the back of the lens system is called the exit pupil...
) is unity.
Although this assumption usually is reasonable for large-format lenses, it
often is invalid for medium- and small-format lenses.
When
 , the DOF for an asymmetrical lens is
, the DOF for an asymmetrical lens is
where
 is the pupil magnification. When the
is the pupil magnification. When thepupil magnification is unity, this equation reduces to that for a
symmetrical lens.
Except for close-up and macro photography, the effect of lens asymmetry is
minimal. At unity magnification, however, the errors from neglecting the
pupil magnification can be significant. Consider a telephoto lens with
 and a retrofocus wide-angle lens with
and a retrofocus wide-angle lens with  , at
, at  . The asymmetrical-lens formula gives
. The asymmetrical-lens formula gives and
and  ,
,respectively. The symmetrical-lens formula gives
 in either case. The errors are −33% and 33%, respectively.
in either case. The errors are −33% and 33%, respectively.Focus and f-number from DOF limits
For given nearand far DOF limits
 and
and  ,
,the required f-number
F-number
In optics, the f-number of an optical system expresses the diameter of the entrance pupil in terms of the focal length of the lens; in simpler terms, the f-number is the focal length divided by the "effective" aperture diameter...
is smallest when focus is set to

the harmonic mean
Harmonic mean
In mathematics, the harmonic mean is one of several kinds of average. Typically, it is appropriate for situations when the average of rates is desired....
of the near and far distances. When the subject distance is large in comparison with the lens focal
length, the required f-number is

When the far limit of DOF is at infinity,

and

In practice, these settings usually are determined on the image side of the
lens, using measurements on the bed or rail with a view camera, or using
lens DOF scales on manual-focus lenses for small- and medium-format
cameras. If
 and
and 
are the image distances that correspond to the near and far limits of DOF,
the required f-number is minimized when the image distance
 is
is
In practical terms, focus is set to halfway between the near and far
image distances. The required f-number is

The image distances are measured from the camera's image plane to the
lens's image nodal plane, which is not always easy to locate. In most
cases, focus and f-number can be determined with sufficient
accuracy using the approximate formulas above, which require only the
difference between the near and far image distances;
view camera users sometimes refer to the difference
 as the focus spread
as the focus spread(Hansma 1996, 55). Most lens DOF scales are based on the same concept.
The focus spread is related to the depth of focus
Depth of focus
Depth of focus is a lens optics concept that measures the tolerance of placement of the image plane in relation to the lens...
. Ray (2000, 56)
gives two definitions of the latter. The first is the tolerance of the position of the image plane
for which an object remains acceptably sharp; the second is that the limits of depth of focus
are the image-side conjugates of the near and far limits of DOF. With the first definition,
focus spread and depth of focus are usually close in value though conceptually different.
With the second definition, focus spread and depth of focus are the same.
Foreground and background blur
If a subject is at distance and the foreground or background is at distance
and the foreground or background is at distance , let the distance between the subject and the foreground or background be
, let the distance between the subject and the foreground or background beindicated by

The blur disk diameter
 of a detail at distance
of a detail at distance 
from the subject can be expressed as a function of the focal length
 , subject magnification
, subject magnification  , and
, andf-number
 according to
according to
The minus sign applies to a foreground object, and the plus sign applies to a background object.
The blur increases with the distance from the subject; when
 , the detail
, the detailis within the depth of field, and the blur is imperceptible. If the detail is only slightly
outside the DOF, the blur may be only barely perceptible.
For a given subject magnification, f-number, and distance from the subject
of the foreground or background detail, the degree of detail blur varies with the lens focal length.
For a background detail, the blur increases with focal length; for a foreground detail,
the blur decreases with focal length. For a given scene, the positions of the subject,
foreground, and background usually are fixed, and the distance between subject and the
foreground or background remains constant regardless of the camera position; however, to maintain
constant magnification, the subject distance must vary if the focal length is changed.
For small distance between the foreground or background detail, the effect of focal length is small;
for large distance, the effect can be significant. For a reasonably distant background detail,
the blur disk diameter is

depending only on focal length.
The blur diameter of foreground details is very large if the details are close to the lens.
The magnification of the detail also varies with focal length; for a given detail,
the ratio of the blur disk diameter to imaged size of the detail is independent of focal length,
depending only on the detail size and its distance from the subject. This ratio can be useful
when it is important that the background be recognizable (as usually is the case in evidence or
surveillance photography), or unrecognizable (as might be the case for a pictorial photographer
using selective focus to isolate the subject from a distracting background). As a general rule,
an object is recognizable if the blur disk diameter is one-tenth to one-fifth the size of the object
or smaller (Williams 1990, 205),
and unrecognizable when the blur disk diameter is the object size or greater.
The effect of focal length on background blur is illustrated in van Walree's article on
Depth of field.
Practical complications
The distance scales on most medium- and small-format lenses indicatedistance from the camera’s image plane
Film plane
A film plane is the area inside any image taking device with a lens and a digital sensor or film; such as a camera. The film plane varies in distance from the lens focal point in each manufacturer...
. Most DOF
formulas, including those in this article, use the object distance
 from the lens’s front nodal plane,
from the lens’s front nodal plane,which often is not easy to
locate. Moreover, for many zoom lenses and internal-focusing non-zoom
lenses, the location of the front nodal plane, as well as focal length,
changes with subject distance. When the subject distance is large in
comparison with the lens focal length, the exact location of the front
nodal plane is not critical; the distance is essentially the same whether
measured from the front of the lens, the image plane, or the actual nodal
plane. The same is not true for close-up photography; at unity
magnification, a slight error in the location of the front nodal plane can
result in a DOF error greater than the errors from any approximations in
the DOF equations.
The asymmetrical lens formulas require knowledge of the
pupil magnification
Pupil magnification
The pupil magnification of an optical system is the ratio of the diameter of the exit pupil to the diameter of the entrance pupil. The pupil magnification is used in calculations of the effective f-number, which affects a number of important elements related to optics, such as exposure,...
, which usually is not specified for medium- and
small-format lenses. The pupil magnification can be estimated by looking
into the front and rear of the lens and measuring the diameters of the
apparent apertures, and computing the ratio of rear diameter to front
diameter (Shipman 1977, 144).
However, for many zoom lenses and internal-focusing non-zoom lenses, the
pupil magnification changes with subject distance, and several measurements
may be required.
Limitations
Most DOF formulas, including those discussed in this article, employseveral simplifications:
- ParaxialParaxial approximationIn geometric optics, the paraxial approximation is a small-angle approximation used in Gaussian optics and ray tracing of light through an optical system ....
(GaussianGaussian opticsGaussian optics is a technique in geometrical optics that describes the behaviour of light rays in optical systems by using the paraxial approximation, in which only rays which make small angles with the optical axis of the system are considered. In this approximation, trigonometric functions can...
) optics is assumed, and technically, the formulas are valid only for rays that are infinitesimally close to the lens axis. However, Gaussian optics usually is more than adequate for determining DOF, and non-paraxial formulas are sufficiently complex that requiring their use would make determination of DOF impractical in most cases. - Lens aberrationsAberration in optical systemsAberrations are departures of the performance of an optical system from the predictions of paraxial optics. Aberration leads to blurring of the image produced by an image-forming optical system. It occurs when light from one point of an object after transmission through the system does not converge...
are ignored. Including the effects of aberrations is nearly impossible, because doing so requires knowledge of the specific lens design. Moreover, in well-designed lenses, most aberrations are well corrected, and at least near the optical axisOptical axisAn optical axis is a line along which there is some degree of rotational symmetry in an optical system such as a camera lens or microscope.The optical axis is an imaginary line that defines the path along which light propagates through the system...
, often are almost negligible when the lens is stopped down 2–3 steps from maximum apertureApertureIn optics, an aperture is a hole or an opening through which light travels. More specifically, the aperture of an optical system is the opening that determines the cone angle of a bundle of rays that come to a focus in the image plane. The aperture determines how collimated the admitted rays are,...
. Because lenses usually are stopped down at least to this point when DOF is of interest, ignoring aberrations usually is reasonable. Not all aberrations are reduced by stopping down, however, so actual sharpness may be slightly less than predicted by DOF formulas. - DiffractionDiffractionDiffraction refers to various phenomena which occur when a wave encounters an obstacle. Italian scientist Francesco Maria Grimaldi coined the word "diffraction" and was the first to record accurate observations of the phenomenon in 1665...
is ignored. DOF formulas imply that any arbitrary DOF can be achieved by using a sufficiently large f-numberF-numberIn optics, the f-number of an optical system expresses the diameter of the entrance pupil in terms of the focal length of the lens; in simpler terms, the f-number is the focal length divided by the "effective" aperture diameter...
. Because of diffraction, however, this isn't really true, as is discussed further in the section DOF and diffraction. - For digital capture with color filter array sensors, demosaicingDemosaicingA demosaicing algorithm is a digital image process used to reconstruct a full color image from the incomplete color samples output from an image sensor overlaid with a color filter array...
is ignored. Demosaicing alone would normally decrease sharpness, but the demosaicing algorithm used might also include sharpening. - Post-capture manipulation of the image is ignored. Sharpening via techniques such as deconvolutionDeconvolutionIn mathematics, deconvolution is an algorithm-based process used to reverse the effects of convolution on recorded data. The concept of deconvolution is widely used in the techniques of signal processing and image processing...
or unsharp mask can increase the apparent sharpness in the final image; conversely, image noise reduction can reduce sharpness. - The resolutions of the imaging medium and the display medium are ignored. If the resolution of either medium is of the same order of magnitude as the optical resolution, the sharpness of the final image is reduced, and optical blurring is harder to detect.
The lens designer cannot restrict analysis to Gaussian optics and cannot
ignore lens aberrations. However, the requirements of practical
photography are less demanding than those of lens design, and despite the
simplifications employed in development of most DOF formulas, these
formulas have proven useful in determining camera settings that result in
acceptably sharp pictures. It should be recognized that DOF limits are not
hard boundaries between sharp and unsharp, and that there is little point
in determining DOF limits to a precision of many significant figures.
DOF and diffraction
If the camera position and image framing (i.e., angle of view) have beenchosen, the only means of controlling DOF is the lens aperture. Most DOF formulas imply that any arbitrary DOF can be achieved by using a sufficiently large f-number
F-number
In optics, the f-number of an optical system expresses the diameter of the entrance pupil in terms of the focal length of the lens; in simpler terms, the f-number is the focal length divided by the "effective" aperture diameter...
. Because of diffraction, however, this isn't really true. Once a lens is stopped down to where most aberrations are well corrected, stopping down further will decrease sharpness in the plane of focus. At the DOF limits, however, further stopping down decreases the size of the defocus
Defocus aberration
In optics, defocus is the aberration in which an image is simply out of focus. This aberration is familiar to anyone who has used a camera, videocamera, microscope, telescope, or binoculars. Optically, defocus refers to a translation along the optical axis away from the plane or surface of best...
blur spot, and the overall sharpness may still increase. Eventually, the defocus blur spot becomes negligibly small, and further stopping down serves only to decrease sharpness even at DOF limits (Gibson 1975, 64).
There is thus a tradeoff between sharpness in the POF and sharpness at the DOF limits. But the sharpness in the POF is always greater than that at the DOF limits; if the blur at the DOF limits is imperceptible, the blur in the POF is imperceptible as well.
For general photography, diffraction at DOF limits typically becomes significant only at fairly large f-numbers; because large f-numbers typically require long exposure times, motion blur
Motion blur
Motion blur is the apparent streaking of rapidly moving objects in a still image or a sequence of images such as a movie or animation. It results when the image being recorded changes during the recording of a single frame, either due to rapid movement or long exposure.- Photography :When a camera...
may cause greater loss of sharpness than the loss from diffraction. The size of the diffraction blur spot depends on the effective f-number
 , however, so diffraction is a greater issue in close-up photography, and the tradeoff between DOF and overall sharpness can become quite noticeable (Gibson 1975, 53; Lefkowitz 1979, 84).
, however, so diffraction is a greater issue in close-up photography, and the tradeoff between DOF and overall sharpness can become quite noticeable (Gibson 1975, 53; Lefkowitz 1979, 84).Optimal f-number
As a lens is stopped down, the defocus blur at the DOF limits decreases but diffraction blur increases. The presence of these two opposing factors implies a point at which the combined blur spot is minimized (Gibson 1975, 64); at that point, the f-number is optimal for image sharpness.If the final image is viewed under normal conditions (e.g., an 8″×10″ image viewed at 10″), it may suffice to determine the f-number using criteria for minimum required sharpness, and there may be no practical benefit from further reducing the size of the blur spot. But this may not be true if the final image is viewed under more demanding conditions, e.g., a very large final image viewed at normal distance, or a portion of an image enlarged to normal size (Hansma 1996). Hansma also suggests that the final-image size may not be known when a photograph is taken, and obtaining the maximum practicable sharpness allows the decision to make a large final image to be made at a later time.
Determining combined defocus and diffraction
Hansma (1996) and Peterson (1996)have discussed determining the combined effects of defocus and diffraction
using a root-square combination of the individual blur spots. Hansma's approach determines
the f-number that will give the maximum possible sharpness; Peterson's approach
determines the minimum f-number that will give the desired sharpness in the
final image, and yields a maximum focus spread for which the desired sharpness can be achieved.
In combination, the two methods can be regarded as giving a maximum and minimum
f-number for a given situation, with the photographer free to choose any value within the range, as conditions (e.g., potential motion blur) permit.
Gibson (1975, 64) gives a similar discussion,
additionally considering blurring effects of camera lens aberrations, enlarging lens
diffraction and aberrations, the negative emulsion, and the printing
paper.
Couzin (1982, 1098) gives a formula essentially the same as Hansma’s for optimal f-number, but does not discuss its derivation.
Hopkins (1955),
Stokseth (1969), and
Williams and Becklund (1989)
have discussed the combined effects using the modulation transfer function.
Conrad's Depth of Field in Depth (PDF), and Jacobson's Photographic Lenses Tutorial discuss the use of Hopkins's method specifically in regard to DOF.
Photolithography
In semiconductorSemiconductor
A semiconductor is a material with electrical conductivity due to electron flow intermediate in magnitude between that of a conductor and an insulator. This means a conductivity roughly in the range of 103 to 10−8 siemens per centimeter...
photolithography
Photolithography
Photolithography is a process used in microfabrication to selectively remove parts of a thin film or the bulk of a substrate. It uses light to transfer a geometric pattern from a photomask to a light-sensitive chemical "photoresist", or simply "resist," on the substrate...
applications, depth of field is extremely important as integrated circuit
Integrated circuit
An integrated circuit or monolithic integrated circuit is an electronic circuit manufactured by the patterned diffusion of trace elements into the surface of a thin substrate of semiconductor material...
layout features must be printed with high accuracy at extremely small size. The difficulty is that the wafer
Wafer (electronics)
A wafer is a thin slice of semiconductor material, such as a silicon crystal, used in the fabrication of integrated circuits and other microdevices...
surface is not perfectly flat, but may vary by several micrometre
Micrometre
A micrometer , is by definition 1×10-6 of a meter .In plain English, it means one-millionth of a meter . Its unit symbol in the International System of Units is μm...
s. Even this small variation causes some distortion in the projected image, and results in unwanted variations in the resulting pattern. Thus photolithography engineers take extreme measures to maximize the optical depth of field of the photolithography equipment. To minimize this distortion further, semiconductor manufacturers may use chemical mechanical polishing to make the wafer surface even flatter before lithographic patterning.
Ophthalmology and optometry
A person may sometimes experience better vision in daylight than at night because of an increased depth of field due to constriction of the pupilPupil
The pupil is a hole located in the center of the iris of the eye that allows light to enter the retina. It appears black because most of the light entering the pupil is absorbed by the tissues inside the eye. In humans the pupil is round, but other species, such as some cats, have slit pupils. In...
(i.e., miosis
Miosis
Miosis is the constriction of the pupil of the eye to two millimeters or less...
).
Digital techniques for extending DOF
Focus stacking
Focus stackingFocus stacking
Focus stacking is a digital image processing technique which combines multiple images taken at different focus distances to give a resulting image with a greater depth of field than any of the individual source images...
is a digital image processing
Digital image processing
Digital image processing is the use of computer algorithms to perform image processing on digital images. As a subcategory or field of digital signal processing, digital image processing has many advantages over analog image processing...
technique which combines multiple images taken at different focus distances to give a resulting image with a greater depth of field than any of the individual source images. Available programs for multi-shot DOF enhancement include Adobe Photoshop, Syncroscopy AutoMontage, PhotoAcute Studio, Helicon Focus
Helicon Focus
Helicon Focus is a proprietary commercial digital image processing tool, first released in 2003, developed and published by Helicon Soft Limited...
and CombineZM
CombineZM
CombineZM is an open source image processing software package for creating extended depth of field images. It runs on Windows XP and 2000. CombineZM is based on CombineZ5, a program which runs on older versions of Windows and is no longer maintained...
.
Getting sufficient depth of field can be particularly challenging in macro photography. The images to the right illustrate the extended DOF that can be achieved by combining multiple images.
Wavefront coding
Wavefront codingWavefront coding
In optics and signal processing, wavefront coding is a method for creating optical transfer functions of lenses with specially designed phase masks, encoding, to produce point spread functions of visible light, images, with manipulatable information such as depth of field and distance.Wavefront...
is a method that convolves rays in such a way that it provides an image where fields are in focus simultaneously with all planes out of focus by a constant amount.
Plenoptic cameras
A plenoptic cameraPlenoptic camera
A light-field camera, also called a plenoptic camera, is a camera that uses a microlens array to capture 4D light field information about a scene...
uses a microlens array to capture 4D light field information about a scene.
Derivation of the DOF formulas
DOF limits
A symmetrical lens is illustrated at right. The subject, at distance , is in focus at image distance
, is in focus at image distance  . Point objects
. Point objectsat distances
 and
and  would be
would bein focus at image distances
 and
and  , respectively; at image distance
, respectively; at image distance  , they are imaged
, they are imagedas blur spots. The depth of field is controlled by the aperture stop
diameter
 ; when the blur spot diameter is equal to the
; when the blur spot diameter is equal to theacceptable circle of confusion
Circle of confusion
In optics, a circle of confusion is an optical spot caused by a cone of light rays from a lens not coming to a perfect focus when imaging a point source...
 , the near and far limits
, the near and far limitsof DOF are at
 and
and  . From
. Fromsimilar triangles,

and

It usually is more convenient to work with the lens f-number
than the aperture diameter; the f-number
 is
isrelated to the lens focal length
 and the aperture diameter
and the aperture diameter by
by
substitution into the previous equations gives

Rearranging to solve for
 and
and  gives
gives
and

The image distance
 is related to an object distance
is related to an object distance by the thin lens
by the thin lensThin lens
[Image:Lens1.svg|thumb|A lens can be considered a thin lens if d [Image:Lens1.svg|thumb|A lens can be considered a thin lens if d [Image:Lens1.svg|thumb|A lens can be considered a thin lens if d...
equation

applying this to
 and
and  gives
gives
and

solving for
 ,
,  , and
, and  in these three equations, substituting into the two previous equations, and rearranging gives the near and far limits of DOF:
in these three equations, substituting into the two previous equations, and rearranging gives the near and far limits of DOF:
and

Hyperfocal distance
Solving for the focus distance and setting the far limit of DOF
and setting the far limit of DOF to infinity gives
to infinity gives
where
 is the hyperfocal distance
is the hyperfocal distanceHyperfocal distance
In optics and photography, hyperfocal distance is a distance beyond which all objects can be brought into an "acceptable" focus. There are two commonly used definitions of hyperfocal distance, leading to values that differ only slightly:...
. Setting the subject
distance to the hyperfocal distance and solving for the near limit of DOF
gives

For any practical value of
 , the focal length is negligible
, the focal length is negligiblein comparison, so that

Substituting the approximate expression for hyperfocal distance into the
formulas for the near and far limits of DOF gives

and

Combining, the depth of field
 is
is
Hyperfocal magnification
Magnification can be expressed as
can be expressed as
at the hyperfocal distance, the magnification
 then is
then is
Substituting
 for
for  and simplifying gives
and simplifying gives
DOF in terms of magnification
It is sometimes convenient to express DOF in terms of magnification m. Substituting
and

into the formula for DOF and rearranging gives

after Larmore (1965, 163).
DOF vs. focal length
Multiplying the numerator anddenominator of the exact formula above by

gives

If the f-number and circle of confusion are constant,
decreasing the focal length
 increases the second term in the
increases the second term in thedenominator, decreasing the denominator and increasing the value of the
right-hand side, so that a shorter focal length gives greater DOF.
The term in parentheses in the denominator is the hyperfocal magnification
 , so that
, so that
A subject distance is decreased, the subject magnification increases, and eventually
becomes large in comparison with the hyperfocal magnification.
Thus the effect of focal length is greatest near the hyperfocal distance, and
decreases as subject distance is decreased. However, the near/far
perspective will differ for different focal lengths, so the difference in
DOF may not be readily apparent.
When
 ,
,  , and
, and
so that for a given magnification, DOF is essentially independent of focal length.
Stated otherwise, for the same subject magnification and the same f-number, all focal lengths for
a given image format
Film format
A film format is a technical definition of a set of standard characteristics regarding image capture on photographic film, for either stills or movies. It can also apply to projected film, either slides or movies. The primary characteristic of a film format is its size and shape.In the case of...
give approximately the same DOF. This
statement is true only when the subject distance is small in comparison
with the hyperfocal distance, however.
Moderate-to-large distances
When the subject distance is large in comparison with the lens focal lengthFocal length
The focal length of an optical system is a measure of how strongly the system converges or diverges light. For an optical system in air, it is the distance over which initially collimated rays are brought to a focus...
,

and

so that

For
 , the far limit of DOF is at infinity and the DOF
, the far limit of DOF is at infinity and the DOFis infinite; of course, only objects at or beyond the near limit of DOF
will be recorded with acceptable sharpness.
Close-up
When the subject distance approaches the lens focal length,
approaches the lens focal length,the focal length no longer is negligible, and the approximate formulas
above cannot be used without introducing significant error. At close
distances, the hyperfocal distance has little applicability, and it usually
is more convenient to express DOF in terms of magnification. The distance
is small in comparison with the hyperfocal distance, so the simplified formula

can be used with good accuracy. For a given magnification,
DOF is independent of focal length.
Near:far DOF ratio
From the “exact” equations for near and far limits of DOF, the DOF in front of the subject is
and the DOF beyond the subject is

The near:far DOF ratio is

This ratio is always less than unity; at moderate-to-large subject distances,
 , and
, and
When the subject is at the hyperfocal distance or beyond, the far DOF is infinite, and the near:far ratio is zero. It’s commonly stated that approximately 1/3 of the DOF is in front of the subject and approximately 2/3 is beyond; however, this is true only when
 .
.At closer subject distances, it’s often more convenient to express the DOF ratio in terms of the magnification

substitution into the “exact” equation for DOF ratio gives

As magnification increases, the near:far ratio approaches a limiting value of unity.
DOF vs. format size
When the subject distance is much less than hyperfocal, the total DOF is given to good approximation by
When additionally the magnification is small compared to unity, the value of
 in the numerator can be neglected, and the formula further simplifies to
in the numerator can be neglected, and the formula further simplifies to
The DOF ratio for two different formats is then

Essentially the same approach is described in Stroebel (1976, 136–39).
“Same picture” for both formats
The results of the comparison depend on what is assumed. One approach is to assume that essentially the same picture is taken with each format and enlarged to produce the same size final image, so the subject distance remains the same, the focal length is adjusted to maintain the same angle of view, and to a first approximation, magnification is in direct proportion to some characteristic dimension of each format. If both pictures are enlarged to give the same size final images with the same sharpness criteria, the circle of confusion is also in direct proportion to the format size. Thus if is the characteristic dimension of the format,
is the characteristic dimension of the format,
With the same f-number, the DOF ratio is then

so the DOF ratio is in inverse proportion to the format size. This ratio is approximate, and breaks down in the macro range of the larger format (the value of
 in the numerator is no longer negligible) or as distance approaches the hyperfocal distance for the smaller format (the DOF of the smaller format approaches infinity).
in the numerator is no longer negligible) or as distance approaches the hyperfocal distance for the smaller format (the DOF of the smaller format approaches infinity).If the formats have approximately the same aspect ratios, the characteristic dimensions can be the format diagonals; if the aspect ratios differ considerably (e.g., 4×5 vs. 6×17), the dimensions must be chosen more carefully, and the DOF comparison may not even be meaningful.
If the DOF is to be the same for both formats the required f-number is in direct proportion to the format size:

Adjusting the f-number in proportion to format size is equivalent to using the same absolute aperture diameter for both formats, discussed in detail below in Use of absolute aperture diameter.
Same focal length for both formats
If the same lens focal length is used in both formats, magnifications can be maintained in the ratio of the format sizes by adjusting subject distances; the DOF ratio is the same as that given above, but the images differ because of the different perspectives and angles of view.If the same DOF is required for each format, an analysis similar to that above shows that the required f-number is in direct proportion to the format size.
Another approach is to use the same focal length with both formats at the same subject distance, so the magnification is the same, and with the same f-number,

so the DOF ratio is in direct proportion to the format size. The perspective is the same for both formats, but because of the different angles of view, the pictures are not the same.
Cropping
Cropping an image and enlarging to the same size final image as an uncropped image taken under the same conditions is equivalent to using a smaller format; the cropped image requires greater enlargement and consequently has a smaller circle of confusion. The cropped image has less DOF than the uncropped image.Use of absolute aperture diameter
The aperture diameter is normally given in terms of the f-number because all lenses set to the same f-number give approximately the same image illuminanceIlluminance
In photometry, illuminance is the total luminous flux incident on a surface, per unit area. It is a measure of the intensity of the incident light, wavelength-weighted by the luminosity function to correlate with human brightness perception. Similarly, luminous emittance is the luminous flux per...
(Ray 2002, 130), simplifying exposure settings. In deriving the basic DOF equations, the substitution of
 for the absolute aperture diameter
for the absolute aperture diameter  can be omitted, giving the DOF in terms of the absolute aperture diameter:
can be omitted, giving the DOF in terms of the absolute aperture diameter:
after Larmore (1965, 163). When the subject distance
 is small in comparison with the hyperfocal distance, the second term in the denominator can be neglected, leading to
is small in comparison with the hyperfocal distance, the second term in the denominator can be neglected, leading to
With the same subject distance and angle of view for both formats,
 , and
, and
so the DOFs are in inverse proportion to the absolute aperture diameters. When the diameters are the same, the two formats have the same DOF. Von Rohr (1906) made this same observation, saying “At this point it will be sufficient to note that all these formulae involve quantities relating exclusively to the entrance-pupil and its position with respect to the object-point, whereas the focal length of the transforming system does not enter into them.” Lyon’s Depth of Field Outside the Box describes an approach very similar to that of von Rohr
Moritz von Rohr
Moritz von Rohr was an optical scientist at Carl Zeiss in Jena.A street in Jena is named after him: Moritz-von-Rohr-Straße, near Carl-Zeiss-Promenade and Otto-Schott-Straße, reminders of the proud optical heritage of the city.-Life:...
.
Using the same absolute aperture diameter for both formats with the “same picture” criterion is equivalent to adjusting the f-number in proportion to the format sizes, discussed above under “Same picture” for both formats
Object-side relationships
The equations forthe DOF limits can be combined to eliminate
 and solve for
and solve forthe subject distance. For given near and far DOF limits
 and
and  , the
, thesubject distance is

the harmonic mean
Harmonic mean
In mathematics, the harmonic mean is one of several kinds of average. Typically, it is appropriate for situations when the average of rates is desired....
of the near and far distances. The equations for DOF limits also can be combined to eliminate
 and solve for the required f-number, giving
and solve for the required f-number, giving
When the subject distance is large in comparison with the lens focal
length, this simplifies to

When the far limit of DOF is at infinity, the equations for
 and
and  give indeterminate results. But if all terms in the numerator and denominator on the right-hand side of the equation for
give indeterminate results. But if all terms in the numerator and denominator on the right-hand side of the equation for  are divided by
are divided by  , it is seen that when
, it is seen that when  is at infinity,
is at infinity,
Similarly, if all terms in the numerator and denominator on the right-hand side of the equation for
 are divided by
are divided by  , it is seen that when
, it is seen that when  is at infinity,
is at infinity,
Image-side relationships
Most discussions of DOF concentrate on the object side of the lens,but the formulas are simpler and the measurements usually easier to make on the
image side. If the basic image-side equations

and

are combined and solved for the image distance
 , the result is
, the result is
the harmonic mean of the near and far image distances. The basic image-side equations can also be combined and solved for
 , giving
, giving
The image distances are measured from the camera's image plane to the
lens's image nodal plane, which is not always easy to locate. The harmonic mean is always less than the arithmentic mean, but when the difference between the near and far image distances is reasonably small, the two means are close to equal, and focus can be set with sufficient accuracy using

This formula requires only the difference
 between the near and far image distances.
between the near and far image distances.View camera users often refer to this difference as the focus spread;
it usually is measured on the bed or focusing rail.
Focus is simply set to halfway between the near and far image distances.
Substituting
 into the equation for
into the equation for  and rearranging gives
and rearranging gives
One variant of the thin-lens equation is
 , where
, where  is the magnification; substituting this into the equation for
is the magnification; substituting this into the equation for  gives
gives
At moderate-to-large subject distances,
 is small compared to unity, and the
is small compared to unity, and thef-number can often be determined with sufficient accuracy using

For close-up photography, the magnification cannot be ignored, and the f-number should be determined using the first approximate formula.
As with the approximate formula for
 , the approximate formulas for
, the approximate formulas for require only the focus spread
require only the focus spread rather than the absolute image distances.
rather than the absolute image distances.When the far limit of DOF is at infinity,
 .
.On manual-focus small- and medium-format lenses, the focus and f-number
usually are determined using the lens DOF scales, which
often are based on the approximate equations above.
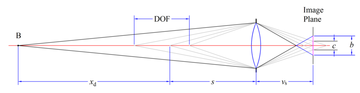
Foreground and background blur
If the equation for the far limit of DOF is solved for , and the far distance
, and the far distancereplaced by an arbitrary distance
 , the blur disk diameter
, the blur disk diameter at that distance is
at that distance is
When the background is at the far limit of DOF, the blur disk diameter is equal to the circle
of confusion
 , and the blur is just imperceptible. The diameter of the background
, and the blur is just imperceptible. The diameter of the backgroundblur disk increases with the distance to the background. A similar relationship holds for the
foreground; the general expression for a defocused object at distance
 is
is
For a given scene, the distance between the subject and a foreground or background object is usually
fixed; let that distance be represented by

then

or, in terms of subject distance,

with the minus sign used for foreground objects and the plus sign used for background objects.
For a relatively distant background object,

In terms of subject magnification, the subject distance is

so that, for a given f-number and subject magnification,

Differentiating
 with respect to
with respect to  gives
gives
With the plus sign, the derivative is everywhere positive,
so that for a background object, the blur disk size increases with focal length.
With the minus sign, the derivative is everywhere negative,
so that for a foreground object, the blur disk size decreases with focal length.
The magnification of the defocused object also varies with focal length; the magnification of the
defocused object is

where
 is the image distance of the subject. For a defocused object
is the image distance of the subject. For a defocused objectwith some characteristic dimension
 , the imaged size of that object is
, the imaged size of that object is
The ratio of the blur disk size to the imaged size of that object then is

so for a given defocused object, the ratio of the blur disk diameter to object size
is independent of focal length, and depends only on the object size and its distance from the subject.
Asymmetrical lenses
The discussion thus far has assumed a symmetrical lens for which theentrance and exit pupil
Pupil
The pupil is a hole located in the center of the iris of the eye that allows light to enter the retina. It appears black because most of the light entering the pupil is absorbed by the tissues inside the eye. In humans the pupil is round, but other species, such as some cats, have slit pupils. In...
s coincide with the object and image
nodal planes, and for which the pupil magnification
Pupil magnification
The pupil magnification of an optical system is the ratio of the diameter of the exit pupil to the diameter of the entrance pupil. The pupil magnification is used in calculations of the effective f-number, which affects a number of important elements related to optics, such as exposure,...
is unity.
Although this assumption usually is reasonable for large-format lenses, it
often is invalid for medium- and small-format lenses.
For an asymmetrical lens, the DOF ahead of the subject distance and the
DOF beyond the subject distance are given by

and

where
 is the pupil magnification.
is the pupil magnification.Combining gives the total DOF:

When
 , the second term in the denominator becomes
, the second term in the denominator becomessmall in comparison with the first, and (Shipman 1977, 147)

When the pupil magnification is unity, the equations for asymmetrical
lenses reduce to those given earlier for symmetrical lenses.
Effect of lens asymmetry
Except for close-up and macro photography, the effect of lens asymmetry isminimal. A slight rearrangement of the last equation gives

As magnification decreases, the
 term becomes smaller in
term becomes smaller incomparison with the
 term, and eventually the effect of
term, and eventually the effect ofpupil magnification becomes negligible.
See also
- Angle of viewAngle of viewIn photography, angle of view describes the angular extent of a given scene that is imaged by a camera. It is used interchangeably with the more general term field of view....
- BokehBokehIn photography, bokeh is the blur, or the aesthetic quality of the blur, in out-of-focus areas of an image, or "the way the lens renders out-of-focus points of light."...
- Circle of confusionCircle of confusionIn optics, a circle of confusion is an optical spot caused by a cone of light rays from a lens not coming to a perfect focus when imaging a point source...
- Rayleigh lengthRayleigh lengthIn optics and especially laser science, the Rayleigh length or Rayleigh range is the distance along the propagation direction of a beam from the waist to the place where the area of the cross section is doubled. A related parameter is the confocal parameter, b, which is twice the Rayleigh length...
- Numerical apertureNumerical apertureIn optics, the numerical aperture of an optical system is a dimensionless number that characterizes the range of angles over which the system can accept or emit light. By incorporating index of refraction in its definition, NA has the property that it is constant for a beam as it goes from one...
- Deep focusDeep focusDeep focus is a photographic and cinematographic technique using a large depth of field. Depth of field is the front-to-back range of focus in an image — that is, how much of it appears sharp and clear. Consequently, in deep focus the foreground, middle-ground and background are all in focus...
- Depth-of-field adapterDepth-of-field adapterA depth-of-field adapter is used to achieve shallow depth of field on a video camera whose fixed lens or interchangeable lens selection is limited or economically prohibitive at providing such effect...
- Depth of focusDepth of focusDepth of focus is a lens optics concept that measures the tolerance of placement of the image plane in relation to the lens...
- Frazier lensFrazier lensThe Frazier lens is a special camera lens designed by photographer Jim Frazier. The Frazier lens provides a massive depth of field, allowing the foreground and background of an image to be in focus. Frazier's lenses have been widely used in Hollywood and wildlife cinematography...
(very deep DOF) - Hyperfocal distanceHyperfocal distanceIn optics and photography, hyperfocal distance is a distance beyond which all objects can be brought into an "acceptable" focus. There are two commonly used definitions of hyperfocal distance, leading to values that differ only slightly:...
- Perspective distortionPerspective distortion (photography)In photography and cinematography, perspective distortion is a warping or transformation of an object and its surrounding area that differs significantly from what the object would look like with a normal focal length, due to the relative scale of nearby and distant features...
- Shallow focusShallow focusShallow focus is a photographic and cinematographic technique incorporating a small depth of field. In shallow focus one plane of the image is in focus while the rest is out of focus. Shallow focus is typically used to emphasize one part of the image over another...
- Tilted plane focusTilted plane focus"Tilted plane photography" is a method of employing focus as a descriptive, narrative or symbolic artistic device. It is distinct from the more simple uses of selective focus which highlight or emphasise a single point in an image, create an atmospheric bokeh, or miniaturise an obliquely-viewed...
(camera movements used to achieve selective focus) - Miniature faking
Further reading
- Hummel, Rob (editor). 2001. American Cinematographer Manual. 8th ed. Hollywood: ASC Press. ISBN 0-935578-15-3
External links
- Depth of Field explanation and comparison photographs
- Depth of Field—the Third Dimension
- DOFMaster Depth of field calculator
- DOFMaster Explanation of why “all focal lengths have approximately the same depth of field” only under certain conditions
- DOFWizard Depth of Field software calculator for iPhone
- Luminous Landscape demonstration that all focal lengths have approximately the same depth of field when f-number and subject image size are maintained
- Carl Zeiss Depth of Field and Bokeh. Camera Lens News #35. April 2010. Accessed 2010-04-13.
- Bob Atkins’s Digital Depth of Field
- Bob Atkins’s DOF and Background Blur Calculator
- Jeff Conrad’s Depth of Field in Depth (PDF). Includes derivations of most DoF formulas
- Joe Englander’s Apparent Depth of Field: Practical Use in Landscape Photography (PDF). Alternative criteria for circle of confusionCircle of confusionIn optics, a circle of confusion is an optical spot caused by a cone of light rays from a lens not coming to a perfect focus when imaging a point source...
- David Jacobson’s Photographic Lenses Tutorial
- Rik Littlefield’s An Introduction to Extended Depth of Field Digital Photography
- Dick Lyon’s Depth of Field Outside the Box (PDF). A format-independent look at DOF
- Justin Snodgrass’s Depth of Field Explained Video.
- Stanford University CS 178 interactive Flash applet on depth of field, with formula and geometric construction.
- Paul van Walree’s Depth of field.
- Paul van Walree’s DOF with Pupil Magnification. Includes derivation
- Kurt Wirz's Depth of Field (Focus stacking)

