
Gassmann triple
Encyclopedia
In mathematics, a Gassmann triple is a group
G together with two faithful actions
on sets X and Y, such that X and Y are not isomorphic
as G-sets but every element of G has the same number of fixed points
on X and Y. They were introduced by .
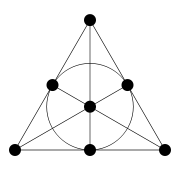 The simple group G = SL3(F2) of order 168 acts on the projective plane of order 2, and the actions on the 7 points and 7 lines give a Gassmann triple.
The simple group G = SL3(F2) of order 168 acts on the projective plane of order 2, and the actions on the 7 points and 7 lines give a Gassmann triple.
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
G together with two faithful actions
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on sets X and Y, such that X and Y are not isomorphic
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
as G-sets but every element of G has the same number of fixed points
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
on X and Y. They were introduced by .
Applications
Gassmann triples have been used to construct examples of pairs of mathematical objects with the same invariants that are not isomorphic, including arithmetically equivalent number fields and isospectral graphs and isospectral Riemannian manifolds.Examples


