.gif)
Cupola (geometry)
Encyclopedia
| Pentagonal cupola (example) | |
|---|---|
 |
|
| Type | Set of cupolas |
| Faces | n triangles, n square Square (geometry) In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles... s 1 n-agon Polygon In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments... , 1 2n-agon |
| Edges | 5n |
| Vertices | 3n |
| Symmetry group Symmetry group The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation... |
Cnv, [1,n], (*nn) |
| Dual polyhedron Dual polyhedron In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another... |
? |
| Properties | convex |
In geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a cupola is a solid formed by joining two polygon
Polygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
s, one (the base) with twice as many edges as the other, by an alternating band of triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
s and rectangle
Rectangle
In Euclidean plane geometry, a rectangle is any quadrilateral with four right angles. The term "oblong" is occasionally used to refer to a non-square rectangle...
s. If the triangles are equilateral and the rectangles are square
Square (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
s, while the base and its opposite face are regular polygons, the triangular
Triangular cupola
In geometry, the triangular cupola is one of the Johnson solids . It can be seen as half a cuboctahedron.The 92 Johnson solids were named and described by Norman Johnson in 1966.-Formulae:...
, square
Square cupola
In geometry, the square cupola, sometimes called lesser dome, is one of the Johnson solids . It can be obtained as a slice of the rhombicuboctahedron...
, and pentagonal
Pentagonal cupola
In geometry, the pentagonal cupola is one of the Johnson solids . It can be obtained as a slice of the rhombicosidodecahedron.The 92 Johnson solids were named and described by Norman Johnson in 1966....
cupolae all count among the Johnson solid
Johnson solid
In geometry, a Johnson solid is a strictly convex polyhedron, each face of which is a regular polygon, but which is not uniform, i.e., not a Platonic solid, Archimedean solid, prism or antiprism. There is no requirement that each face must be the same polygon, or that the same polygons join around...
s, and can be formed by taking sections of the cuboctahedron
Cuboctahedron
In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,...
, rhombicuboctahedron
Rhombicuboctahedron
In geometry, the rhombicuboctahedron, or small rhombicuboctahedron, is an Archimedean solid with eight triangular and eighteen square faces. There are 24 identical vertices, with one triangle and three squares meeting at each. Note that six of the squares only share vertices with the triangles...
, and rhombicosidodecahedron
Rhombicosidodecahedron
In geometry, the rhombicosidodecahedron, or small rhombicosidodecahedron, is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed of two or more types of regular polygon faces....
, respectively.
A cupola can be seen as a prism
Prism (geometry)
In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...
where one of the polygons has been collapsed in half by merging alternate vertices.
Cupolae are a subclass of the prismatoid
Prismatoid
In geometry, a prismatoid is a polyhedron where all vertices lie in two parallel planes....
s.
Examples
 |
|
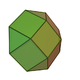 |
 |

Triangular prism
In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides....
might be considered a "cupola" of degree 2 (the cupola of a line segment and a square). However, cupolae of higher-degree polygons may be constructed with irregular triangular and rectangular faces.
Coordinates of the vertices
The definition of the cupola does not require the base (or the side opposite the base, which can be called the top) to be a regular polygon, but it is convenient to consider the case where the cupola has its maximal symmetry, Cnv. In that case, the top is a regular n-gon, while the base is either a regular 2n-gon or a 2n-gon which has two different side lengths alternating and the same angles as a regular 2n-gon. It is convenient to fix the coordinate system so that the base lies in the xy-plane, with the top in a plane parallel to the xy-plane. The z-axis is the n-fold axis, and the mirror planes pass through the z-axis and bisect the sides of the base. They also either bisect the sides or the angles of the top polygon, or both. (If n is even, half of the mirror planes bisect the sides of the top polygon and half bisect the angles, while if n is odd, each mirror plane bisects one side and one angle of the top polygon.) The vertices of the base can be designated V1 through V2n, while the vertices of the top polygon can be designated V2n+1 through V3n. With these conventions, the coordinates of the vertices can be written as:- V2j-1: (rbcos [2π(j-1)/n + α], rbsin [2π(j-1)/n + α], 0)
- V2j: (rbcos (2πj/n - α), rbsin (2πj/n - α), 0)
- V2n+j: (rtcos (πj/n), rtsin (πj/n), h)
where j=1, 2, …, n.
Since the polygons V1V2V2n+2V2n+1, etc. are rectangles, this puts a constraint on the values of rb, rt, and α. The distance V1V2 is equal to
rb{[cos (2π/n - α) – cos α]2 + [sin (2π/n - α) - sin α] 2}1/2
rb{[cos 2 (2π/n - α) – 2cos (2π/n - α)cos α + cos2 α] + [sin 2 (2π/n - α) – 2 sin (2π/n - α)sin α + sin 2α]}1/2
rb{2[1 – cos (2π/n - 2α)]}1/2,
while the distance V2n+1V2n+2 is equal to
rt{[cos (π/n) – 1]2 + sin2(π/n)}1/2
rt{2[1 – cos (π/n)]}1/2.
These are to be equal, and if this common edge is denoted by s,
rb = s/{2[1 – cos (2π/n - 2α)]}1/2
rt= s/{2[1 – cos (π/n)]}1/2
These values are to be inserted into the expressions for the coordinates of the vertices given earlier.
Hypercupolas
The hypercupolas are a family of convex nonuniform polychora (here four-dimensional figures), analogous to the cupolas. Each one's bases are a Platonic solidPlatonic solid
In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
and its expansion
Expansion (geometry)
In geometry, expansion is a polytope operation where facets are separated and moved radially apart, and new facets are formed at separated elements...
.
| Tetrahedral cupola | Cubic cupola | Octahedral cupola | Dodecahedral cupola | Icosahedral cupola | ||||||
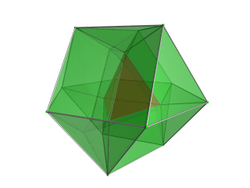 |
 |
 |
||||||||
| Vertices | 16 | 32 | 30 | 80 | 72 | |||||
| Edges | 42 | 84 | 84 | 210 | 210 | |||||
| Faces | 42 | 24 triangle Triangle A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted .... s 18 squares Square (geometry) In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles... |
80 | 32 triangle Triangle A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted .... s 48 squares Square (geometry) In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles... |
82 | 40 triangle Triangle A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted .... s 42 squares Square (geometry) In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles... |
194 | 80 triangle Triangle A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted .... s 90 squares Square (geometry) In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles... 24 pentagon Pentagon In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and... s |
202 | 100 triangle Triangle A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted .... s 90 squares Square (geometry) In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles... 12 pentagon Pentagon In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and... s |
| Cells | 16 | 1 tetrahedron Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... 4 triangular prism Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... s 6 triangular prism Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... s 4 triangular pyramids Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... 1 cuboctahedron Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,... |
28 | 1 cube Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... 6 square prisms Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... 12 triangular prism Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... s 8 triangular pyramids Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... 1 rhombicuboctahedron Rhombicuboctahedron In geometry, the rhombicuboctahedron, or small rhombicuboctahedron, is an Archimedean solid with eight triangular and eighteen square faces. There are 24 identical vertices, with one triangle and three squares meeting at each. Note that six of the squares only share vertices with the triangles... |
28 | 1 octahedron Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... 8 triangular prism Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... s 12 triangular prism Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... s 6 square pyramid Square pyramid In geometry, a square pyramid is a pyramid having a square base. If the apex is perpendicularly above the center of the square, it will have C4v symmetry.- Johnson solid :... s 1 rhombicuboctahedron Rhombicuboctahedron In geometry, the rhombicuboctahedron, or small rhombicuboctahedron, is an Archimedean solid with eight triangular and eighteen square faces. There are 24 identical vertices, with one triangle and three squares meeting at each. Note that six of the squares only share vertices with the triangles... |
64 | 1 dodecahedron 12 pentagonal prism Pentagonal prism In geometry, the pentagonal prism is a prism with a pentagonal base. It is a type of heptahedron with 7 faces, 15 edges, and 10 vertices.- As a semiregular polyhedron :... s 30 triangular prism Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... s 20 triangular pyramids Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... 1 rhombicosidodecahedron Rhombicosidodecahedron In geometry, the rhombicosidodecahedron, or small rhombicosidodecahedron, is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed of two or more types of regular polygon faces.... |
64 | 1 icosahedron Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids.... 20 triangular prism Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... s 30 triangular prism Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... s 12 pentagonal pyramid Pentagonal pyramid In geometry, a pentagonal pyramid is a pyramid with a pentagonal base upon which are erected five triangular faces that meet at a point . Like any pyramid, it is self-dual.... s 1 rhombicosidodecahedron Rhombicosidodecahedron In geometry, the rhombicosidodecahedron, or small rhombicosidodecahedron, is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed of two or more types of regular polygon faces.... |

