
Expansion (geometry)
Encyclopedia
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, expansion is a polytope
Polytope
In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
operation where facets
Facet (mathematics)
A facet of a simplicial complex is a maximal simplex.In the general theory of polyhedra and polytopes, two conflicting meanings are currently jostling for acceptability:...
are separated and moved radially apart, and new facets are formed at separated elements (vertices, edges, etc). Equivalently this operation can be imagined by keeping facets in the same location, but reducing their size.
According to Coxeter, this multidimensional term was defined by Alicia Boole Stott
Alicia Boole Stott
Alicia Boole Stott was the third daughter of George Boole and Mary Everest Boole, born in Cork, Ireland. Before marrying Walter Stott, an actuary, in 1890, she was known as Alicia Boole...
for creating new polytopes, specifically starting from regular polytope
Regular polytope
In mathematics, a regular polytope is a polytope whose symmetry is transitive on its flags, thus giving it the highest degree of symmetry. All its elements or j-faces — cells, faces and so on — are also transitive on the symmetries of the polytope, and are regular polytopes of...
s constructs new uniform polytope
Uniform polytope
A uniform polytope is a vertex-transitive polytope made from uniform polytope facets of a lower dimension. Uniform polytopes of 2 dimensions are the regular polygons....
s.
The expansion operation is symmetric with respects to a regular polytope and its dual. The resulting figure contains the facets of both the regular and regular dual, along with various prismatic facets filling the gaps created between intermediate dimensional elements.
It has somewhat different meanings by dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
, and correspond to reflections from the first and last mirrors in a Wythoff construction
Wythoff construction
In geometry, a Wythoff construction, named after mathematician Willem Abraham Wythoff, is a method for constructing a uniform polyhedron or plane tiling. It is often referred to as Wythoff's kaleidoscopic construction.- Construction process :...
.
By dimension:
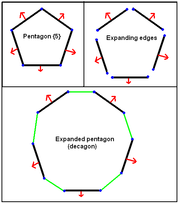
- A regular {p} polygonPolygonIn geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
expands into a regular 2n-gon.- The operation is identical to truncationTruncation (geometry)In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex.- Uniform truncation :...
for polygons, t0,1{p} and has Coxeter-Dynkin diagramCoxeter-Dynkin diagramIn geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
.
- The operation is identical to truncation
- A regular {p,q} polyhedronPolyhedronIn elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
(3-polytope) expands into a polyhedron with vertex figureVertex figureIn geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
p.4.q.4.- This operation for polyhedra is also called cantellationCantellation (geometry)In geometry, a cantellation is an operation in any dimension that cuts a regular polytope at its edges and vertices, creating a new facet in place of each edge and vertex. The operation also applies to regular tilings and honeycombs...
, t0,2{p,q} and has Coxeter-Dynkin diagramCoxeter-Dynkin diagramIn geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
.-
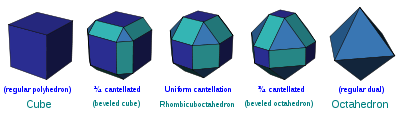
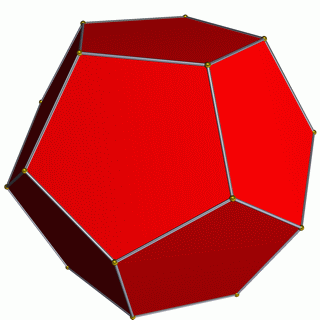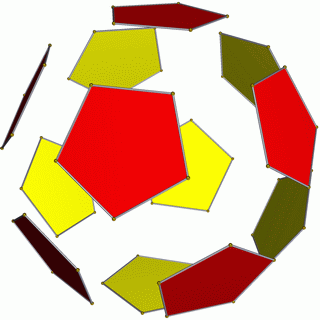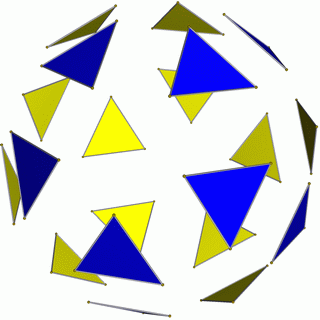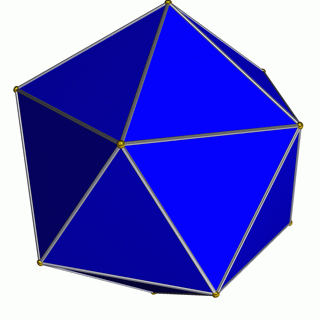
- For example, a rhombicuboctahedron can be called an expanded cube, expanded octahedron, as well as a cantellated cube or cantellated octahedron.
-
- This operation for polyhedra is also called cantellation
- A regular {p,q,r} polychoronPolychoronIn geometry, a polychoron or 4-polytope is a four-dimensional polytope. It is a connected and closed figure, composed of lower dimensional polytopal elements: vertices, edges, faces , and cells...
(4-polytope) expands into a new polychoron with the original {p,q} cells, new cells {r,q} in place of the old vertices, p-gonal prisms in place of the old faces, and r-gonal prisms in place of the old edges.- This operation for polychora is also called runcination, t0,3{p,q,r} and has Coxeter-Dynkin diagramCoxeter-Dynkin diagramIn geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
.
- This operation for polychora is also called runcination, t0,3{p,q,r} and has Coxeter-Dynkin diagram
- Similar a regular {p,q,r,s} polyteron (5-polytope) expands into a new polyteron with facets {p,q,r}, {s,r,q}, {p,q} hyperprisms, {s,r} hyperprisms, and {p}x{s} duoprismDuoprismIn geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher...
s.- This operation is called sterication, t0,4{p,q,r,s} and has Coxeter-Dynkin diagramCoxeter-Dynkin diagramIn geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
.
- This operation is called sterication, t0,4{p,q,r,s} and has Coxeter-Dynkin diagram
The general operator for expansion for an n-polytope is t0,n-1{p,q,r,...}. New simplex
Simplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
facets are added at each vertex, and new prismatic polytopes are added at each divided edge, face, ... ridge
Ridge (geometry)
In geometry, a ridge is an -dimensional element of an n-dimensional polytope. It is also sometimes called a subfacet for having one lower dimension than a facet.By dimension, this corresponds to:*a vertex of a polygon;...
, etc.

