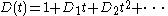Milnor–Thurston kneading theory
Encyclopedia
The Milnor–Thurston kneading theory is a mathematical
theory which analyzes the iterates of piecewise monotone mappings
of an interval
into itself. The emphasis is on understanding the properties of the mapping that are invariant under topological conjugacy.
The theory had been developed by John Milnor
and William Thurston
in two widely circulated and influential Princeton preprints from 1977 that were revised in 1981 and finally published in 1988. Applications of the theory include piecewise linear models, counting of fixed points
, computing the total variation, and constructing an invariant measure
with maximal entropy.
of a piecewise monotone
mapping f of a closed interval I of the real line
into itself. Some quantitative invariants of this discrete dynamical system, such as the lap numbers of the iterates and the Artin–Mazur zeta function of f are expressed in terms of certain matrices
and formal power series
.
The basic invariant of f is its kneading matrix, a rectangular matrix with coefficients in the ring Z
with odd integer coefficients. In the simplest case when the map is unimodal, with a maximum at c, each coefficient Dk is either +1 or −1, according to whether the (k + 1)st iterate f k+1 has local maximum or local minimum at c.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
theory which analyzes the iterates of piecewise monotone mappings
Map (mathematics)
In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
of an interval
Interval
Interval may refer to:* Interval , a range of numbers * Interval measurements or interval variables in statistics is a level of measurement...
into itself. The emphasis is on understanding the properties of the mapping that are invariant under topological conjugacy.
The theory had been developed by John Milnor
John Milnor
John Willard Milnor is an American mathematician known for his work in differential topology, K-theory and dynamical systems. He won the Fields Medal in 1962, the Wolf Prize in 1989, and the Abel Prize in 2011. Milnor is a distinguished professor at Stony Brook University...
and William Thurston
William Thurston
William Paul Thurston is an American mathematician. He is a pioneer in the field of low-dimensional topology. In 1982, he was awarded the Fields Medal for his contributions to the study of 3-manifolds...
in two widely circulated and influential Princeton preprints from 1977 that were revised in 1981 and finally published in 1988. Applications of the theory include piecewise linear models, counting of fixed points
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
, computing the total variation, and constructing an invariant measure
Invariant measure
In mathematics, an invariant measure is a measure that is preserved by some function. Ergodic theory is the study of invariant measures in dynamical systems...
with maximal entropy.
Short description
Kneading theory provides an effective calculus for describing the qualitative behavior of the iteratesIterated function
In mathematics, an iterated function is a function which is composed with itself, possibly ad infinitum, in a process called iteration. In this process, starting from some initial value, the result of applying a given function is fed again in the function as input, and this process is repeated...
of a piecewise monotone
Monotonic function
In mathematics, a monotonic function is a function that preserves the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory....
mapping f of a closed interval I of the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
into itself. Some quantitative invariants of this discrete dynamical system, such as the lap numbers of the iterates and the Artin–Mazur zeta function of f are expressed in terms of certain matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
and formal power series
Formal power series
In mathematics, formal power series are a generalization of polynomials as formal objects, where the number of terms is allowed to be infinite; this implies giving up the possibility to substitute arbitrary values for indeterminates...
.
The basic invariant of f is its kneading matrix, a rectangular matrix with coefficients in the ring Z
with odd integer coefficients. In the simplest case when the map is unimodal, with a maximum at c, each coefficient Dk is either +1 or −1, according to whether the (k + 1)st iterate f k+1 has local maximum or local minimum at c.