Cycle graph
Encyclopedia
In graph theory
, a cycle graph or circular graph is a graph
that consists of a single cycle
, or in other words, some number of vertices connected in a closed chain. The cycle graph with n vertices is called Cn. The number of vertices in Cn equals the number of edges, and every vertex has degree
2; that is, every vertex has exactly two edges incident with it.
s for "cycle graph". These include simple cycle graph and cyclic graph, although the latter term is less often used, because it can also refer to graphs which are merely not acyclic
. Among graph theorists, cycle, polygon, or n-gon are also often used. A cycle with an even number of vertices is called an even cycle; a cycle with an odd number of vertices is called an odd cycle.
In addition:
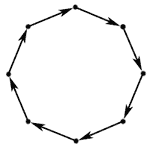A directed cycle graph is a directed version of a cycle graph, with all the edges being oriented in the same direction.
In a directed graph
, a set of edges which contains at least one edge (or arc) from each directed cycle is called a feedback arc set
. Similarly, a set of vertices containing at least one vertex from each directed cycle is called a feedback vertex set
.
A directed cycle graph has uniform in-degree 1 and uniform out-degree 1.
Directed cycle graphs are Cayley graph
s for cyclic group
s (see e.g. Trevisan).
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, a cycle graph or circular graph is a graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
that consists of a single cycle
Path (graph theory)
In graph theory, a path in a graph is a sequence of vertices such that from each of its vertices there is an edge to the next vertex in the sequence. A path may be infinite, but a finite path always has a first vertex, called its start vertex, and a last vertex, called its end vertex. Both of them...
, or in other words, some number of vertices connected in a closed chain. The cycle graph with n vertices is called Cn. The number of vertices in Cn equals the number of edges, and every vertex has degree
Degree (graph theory)
In graph theory, the degree of a vertex of a graph is the number of edges incident to the vertex, with loops counted twice. The degree of a vertex v is denoted \deg. The maximum degree of a graph G, denoted by Δ, and the minimum degree of a graph, denoted by δ, are the maximum and minimum degree...
2; that is, every vertex has exactly two edges incident with it.
Terminology
There are many synonymSynonym
Synonyms are different words with almost identical or similar meanings. Words that are synonyms are said to be synonymous, and the state of being a synonym is called synonymy. The word comes from Ancient Greek syn and onoma . The words car and automobile are synonyms...
s for "cycle graph". These include simple cycle graph and cyclic graph, although the latter term is less often used, because it can also refer to graphs which are merely not acyclic
Directed acyclic graph
In mathematics and computer science, a directed acyclic graph , is a directed graph with no directed cycles. That is, it is formed by a collection of vertices and directed edges, each edge connecting one vertex to another, such that there is no way to start at some vertex v and follow a sequence of...
. Among graph theorists, cycle, polygon, or n-gon are also often used. A cycle with an even number of vertices is called an even cycle; a cycle with an odd number of vertices is called an odd cycle.
Properties
A cycle graph is:- Connected
- 2-regularRegular graphIn graph theory, a regular graph is a graph where each vertex has the same number of neighbors; i.e. every vertex has the same degree or valency. A regular directed graph must also satisfy the stronger condition that the indegree and outdegree of each vertex are equal to each other...
- Eulerian
- Hamiltonian
- 2-vertex colorableBipartite graphIn the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
, if and only if it has an even number of vertices. More generally, a graph is bipartite if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
it has no odd cycles (KőnigDénes KönigDénes Kőnig was a Jewish Hungarian mathematician who worked in and wrote the first textbook on the field of graph theory....
, 1936). - 2-edge colorable, if and only if it has an even number of vertices
- 3-vertex colorable and 3-edge colorable, for any number of vertices
- A unit distance graphUnit distance graphIn mathematics, and particularly geometric graph theory, a unit distance graph is a graph formed from a collection of points in the Euclidean plane by connecting two points by an edge whenever the distance between the two points is exactly one...
In addition:
- As cycle graphs can be drawnGraph drawingGraph drawing is an area of mathematics and computer science combining methods from geometric graph theory and information visualization to derive two-dimensional depictions of graphs arising from applications such as social network analysis, cartography, and bioinformatics...
as regular polygonRegular polygonA regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
s, the symmetries of an n-cycle are the same as those of a regular polygon with n sides, the dihedral groupDihedral groupIn mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
of order 2n. In particular, there exist symmetries taking any vertex to any other vertex, and any edge to any other edge, so the n-cycle is a symmetric graphSymmetric graphIn the mathematical field of graph theory, a graph G is symmetric if, given any two pairs of adjacent vertices u1—v1 and u2—v2 of G, there is an automorphismsuch that...
.
Directed cycle graph
In a directed graph
Directed graph
A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
, a set of edges which contains at least one edge (or arc) from each directed cycle is called a feedback arc set
Feedback arc set
In graph theory, a directed graph may contain directed cycles, a one-way loop of edges. In some applications, such cycles are undesirable, and we wish to eliminate them and obtain a directed acyclic graph . One way to do this is simply to drop edges from the graph to break the cycles...
. Similarly, a set of vertices containing at least one vertex from each directed cycle is called a feedback vertex set
Feedback vertex set
In the mathematical discipline of graph theory, a feedback vertex set of a graph is a set of vertices whose removal leaves a graph without cycles. In other words, each feedback vertex set contains at least one vertex of any cycle in the graph....
.
A directed cycle graph has uniform in-degree 1 and uniform out-degree 1.
Directed cycle graphs are Cayley graph
Cayley graph
In mathematics, a Cayley graph, also known as a Cayley colour graph, Cayley diagram, group diagram, or colour group is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem and uses a specified, usually finite, set of generators for the group...
s for cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
s (see e.g. Trevisan).
See also
- Complete bipartite graphComplete bipartite graphIn the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.- Definition :...
- Path graphPath graphIn the mathematical field of graph theory, a path graph or linear graph is a particularly simple example of a tree, namely a tree with two or more vertices that is not branched at all, that is, contains only vertices of degree 2 and 1...
- Complete graphComplete graphIn the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
- Null graphNull graphIn the mathematical field of graph theory, the null graph may refer either to the order zero graph, or alternatively, to any edgeless graph .-Order zero graph:...
External links
(discussion of both 2-regular cycle graphs and the group-theoretic concept of cycle diagrams)- Luca TrevisanLuca TrevisanLuca Trevisan is a professor of computer science at the University of California, Berkeley. As of winter 2010, he is on leave and an acting professor of computer science at Stanford University....
, Characters and Expansion.