Roulette (curve) - AbsoluteAstronomy.com

Differential geometry of curves

Differential geometry of curves is the branch of geometry that dealswith smooth curves in the plane and in the Euclidean space by methods of differential and integral calculus....

, a roulette is a kind of curve

Curve

In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...

, generalizing cycloid

Cycloid

A cycloid is the curve traced by a point on the rim of a circular wheel as the wheel rolls along a straight line.It is an example of a roulette, a curve generated by a curve rolling on another curve....

s, epicycloid

Epicycloid

In geometry, an epicycloid is a plane curve produced by tracing the path of a chosen point of a circle — called an epicycle — which rolls without slipping around a fixed circle...

s, hypocycloid

Hypocycloid

In geometry, a hypocycloid is a special plane curve generated by the trace of a fixed point on a small circle that rolls within a larger circle...

s, trochoid

Trochoid

thumb|290px|right|A [[cycloid]] generated by a rolling circleTrochoid is the word created by Gilles de Roberval for the curve described by a fixed point as a circle rolls along a straight line...

s, and involute

Involute

In the differential geometry of curves, an involute is a curve obtained from another given curve by attaching an imaginary taut string to the given curve and tracing its free end as it is wound onto that given curve; or in reverse, unwound. It is a roulette wherein the rolling curve is a straight...

s.

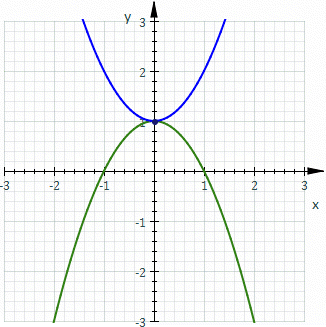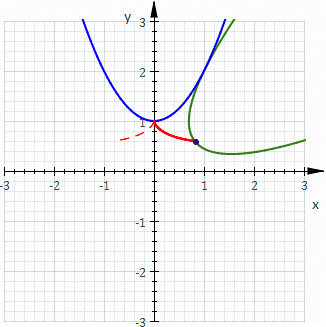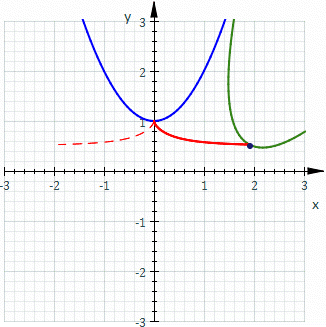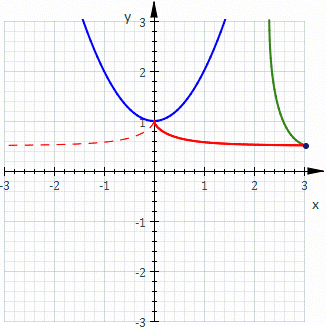
Roughly speaking, it is the curve described by a point (called the generator or pole) attached to a given curve as it rolls without slipping along a second given curve that is fixed. More precisely, given a curve attached to a plane which is moving so that the curve rolls without slipping along a given curve attached to a fixed plane occupying the same space, then a point attached to the moving plane describes a curve in the fixed plane called a roulette.

In the illustration, the fixed curve (blue) is a parabola

Parabola

In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...

, the rolling curve (green) is an equal parabola, and the generator is the vertex of the rolling parabola which describes the roulette (red). In this case the roulette is the cissoid of Diocles

Cissoid of Diocles

In geometry, the cissoid of Diocles is a cubic plane curve notable for the property that it can be used to construct two mean proportionals to a given ratio. In particular, it can be used to double a cube. It can be defined as the cissoid of a circle and a line tangent to it with respect to the...

.

In the case where the rolling curve is a line

Line (geometry)

The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...

and the generator is a point on the line, the roulette is called an involute

Involute

of the fixed curve. If the rolling curve is a circle and the fixed curve is a line then the roulette is a trochoid

Trochoid

thumb|290px|right|A [[cycloid]] generated by a rolling circleTrochoid is the word created by Gilles de Roberval for the curve described by a fixed point as a circle rolls along a straight line...

. If, in this case, the point lies on the circle then the roulette is a cycloid

Cycloid

.

If, instead of a single point being attached to the rolling curve, another given curve is carried along the moving plane, a family of congruent curves is produced. The envelope of this family may also be called a roulette.

A related concept is a glissette, the curve described by a point attached to a given curve as it slides along two (or more) given curves.

Formally speaking, the curves must be differentiable curves in the Euclidean plane. One is kept invariant; the other is subjected to a continuous

Continuous function

In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...

congruence

Congruence (geometry)

In geometry, two figures are congruent if they have the same shape and size. This means that either object can be repositioned so as to coincide precisely with the other object...

transformation such that at all times the curves are tangent

Tangent

In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...

at a point of contact that moves with the same speed when taken along either curve. The resulting roulette is formed by the locus

Locus (mathematics)

In geometry, a locus is a collection of points which share a property. For example a circle may be defined as the locus of points in a plane at a fixed distance from a given point....

of the generator subjected to the same set of congruence transformations.

Modelling the original curves as curves in the complex plane

Complex plane

In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...

, let

be differentiable parametrisations such that r(0)=f(0), r′(0)=f′(0), and |r′(t)|=|f′(t)|≠0 for all t. The roulette of

as r is rolled on f is then given by the mapping:

Roulettes in higher spaces can certainly be imagined but one needs to align more than just the tangents.

Example

If the fixed curve is a catenary

Catenary

In physics and geometry, the catenary is the curve that an idealised hanging chain or cable assumes when supported at its ends and acted on only by its own weight. The curve is the graph of the hyperbolic cosine function, and has a U-like shape, superficially similar in appearance to a parabola...

and the rolling curve is a line

Line (mathematics)

The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...

, we have:

The parameterization of the line is chosen so that

Applying the formula above we obtain:

If p = −i the expression has a constant imaginary part (namely −i) and the roulette is a horizontal line. An interesting application of this is that a square wheel

Square wheel

A square wheel is a wheel that, instead of being circular, has the shape of a square. While literal square wheels exist, a more common use is as a metaphor meaning stereotypically bad or naïve engineering ....

could roll without bouncing on a road that is a matched series of catenary arcs.

List of roulettes

Fixed curve	Rolling curve	Generating point	Roulette
Any curve	Line Line (mathematics) The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...	Point on the line	Involute Involute In the differential geometry of curves, an involute is a curve obtained from another given curve by attaching an imaginary taut string to the given curve and tracing its free end as it is wound onto that given curve; or in reverse, unwound. It is a roulette wherein the rolling curve is a straight... of the curve
Line Line (mathematics) The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...	Circle Circle A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....	Any	Trochoid Trochoid thumb\|290px\|right\|A [[cycloid]] generated by a rolling circleTrochoid is the word created by Gilles de Roberval for the curve described by a fixed point as a circle rolls along a straight line...
Line Line (mathematics) The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...	Circle Circle A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....	Point on the circle	Cycloid Cycloid A cycloid is the curve traced by a point on the rim of a circular wheel as the wheel rolls along a straight line.It is an example of a roulette, a curve generated by a curve rolling on another curve....
Line Line (mathematics) The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...	Conic section Conic section In mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...	Center of the conic	Sturm roulette
Line Line (mathematics) The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...	Conic section Conic section In mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...	Focus Focus (geometry) In geometry, the foci are a pair of special points with reference to which any of a variety of curves is constructed. For example, foci can be used in defining conic sections, the four types of which are the circle, ellipse, parabola, and hyperbola... of the conic	Delaunay roulette
Line Line (mathematics) The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...	Parabola Parabola In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...	Focus Focus (geometry) In geometry, the foci are a pair of special points with reference to which any of a variety of curves is constructed. For example, foci can be used in defining conic sections, the four types of which are the circle, ellipse, parabola, and hyperbola... of the parabola	Catenary Catenary In physics and geometry, the catenary is the curve that an idealised hanging chain or cable assumes when supported at its ends and acted on only by its own weight. The curve is the graph of the hyperbolic cosine function, and has a U-like shape, superficially similar in appearance to a parabola...
Line Line (mathematics) The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...	Ellipse Ellipse In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...	Focus Focus (geometry) In geometry, the foci are a pair of special points with reference to which any of a variety of curves is constructed. For example, foci can be used in defining conic sections, the four types of which are the circle, ellipse, parabola, and hyperbola... of the ellipse	Elliptic catenary
Line Line (mathematics) The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...	Hyperbola Hyperbola In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...	Focus Focus (geometry) In geometry, the foci are a pair of special points with reference to which any of a variety of curves is constructed. For example, foci can be used in defining conic sections, the four types of which are the circle, ellipse, parabola, and hyperbola... of the hyperbola	Hyperbolic catenary
Line Line (mathematics) The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...	Hyperbola Hyperbola In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...	Center Centre (geometry) In geometry, the centre of an object is a point in some sense in the middle of the object. If geometry is regarded as the study of isometry groups then the centre is a fixed point of the isometries.-Circles:... of the hyperbola	Rectangular elastica
Line Line (mathematics) The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...	Epicycloid Epicycloid In geometry, an epicycloid is a plane curve produced by tracing the path of a chosen point of a circle — called an epicycle — which rolls without slipping around a fixed circle... or Hypocycloid Hypocycloid In geometry, a hypocycloid is a special plane curve generated by the trace of a fixed point on a small circle that rolls within a larger circle...	Center	Ellipse Ellipse In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
Circle Circle A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....	Circle Circle A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....	Any	Centered trochoid Centered trochoid In geometry, a centered trochoid is the roulette formed by a circle rolling along another circle. That is, the path traced by a point attached to a circle as the circle rolls without slipping along a fixed circle. The term encompasses both epitrochoid and hypotrochoid...
Parabola Parabola In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...	Equal parabola parameterized in opposite direction	Vertex Vertex (curve) In the geometry of curves, a vertex is a point of where the first derivative of curvature is zero. This is typically a local maximum or minimum of curvature. Other special cases may occur, for instance when the second derivative is also zero, or when the curvature is constant... of the parabola	Cissoid of Diocles Cissoid of Diocles In geometry, the cissoid of Diocles is a cubic plane curve notable for the property that it can be used to construct two mean proportionals to a given ratio. In particular, it can be used to double a cube. It can be defined as the cissoid of a circle and a line tangent to it with respect to the...
Catenary Catenary In physics and geometry, the catenary is the curve that an idealised hanging chain or cable assumes when supported at its ends and acted on only by its own weight. The curve is the graph of the hyperbolic cosine function, and has a U-like shape, superficially similar in appearance to a parabola...	Line Line (mathematics) The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...	See example above	Line

Example

List of roulettes

Further reading