
Caccioppoli set
Encyclopedia
In mathematics
, a Caccioppoli set is a set whose boundary
is measurable and has a (at least locally
) finite measure
. A synonym is set of (locally
) finite perimeter. Basically, a set is a Caccioppoli set if its characteristic function is a function of bounded variation.
in the paper : considering a plane set or a surface
defined on a open set
in the plane
, he defined their measure
or area as the total variation
in the sense of Tonelli
of their defining functions
, i.e. of their parametric equations, provided this quantity was bounded. The measure of the boundary of a set
was defined as a functional
, precisely a set function
, for the first time: also, being defined on open set
s, it can be defined on all Borel set
s and its value can be approximated by the values it takes on an increasing net
of subset
s. Another clearly stated (and demonstrated) property of this functional was its lower semi-continuity
.
In the paper , he made the concept precise by using a triangular mesh
as an increasing net
approximating the open domain, defining positive and negative variations whose sum is the total variation, i.e. the area functional. His inspiring point of view, as he explicitly admitted, was those of Giuseppe Peano
, as expressed by the Peano-Jordan Measure
: associate to every portion of a surface an oriented
plane area in a similar way as an approximating chord
is associated to a curve. Also, another theme found in this theory was the extension of a functional
from a subspace
to the whole ambient space: the use of theorems generalizing the Hahn–Banach theorem
is frequently encountered in Caccioppoli
research. However, the restricted meaning of total variation
in the sense of Tonelli
added much complication to the formal development of the theory, and the use of a parametric description of the sets restricted its scope.
Lamberto Cesari
introduced the "right" generalization of functions of bounded variation
to the case of several variables only in 1936: maybe this was one of the reasons that induced Caccioppoli
to present an improved version of his theory only nearly 24 years later, in the talk at the IV UMI
Congress in October 1951, followed by five notes published in the Rendiconti of the Accademia Nazionale dei Lincei. These notes were sharply criticized by Laurence Chisholm Young
in the Mathematical Reviews
.
In 1952 Ennio de Giorgi
presented to the Salzburg
Congress of the Austrian Mathematical Society his first results related to the ideas of Caccioppoli about the definition of the measure of boundaries of sets: he obtained his results by using a smoothing operator analogous to a mollifier
, constructed from the Gaussian function, proving some results of Caccioppoli
in a different way. Probably he was led to study this theory by his teacher and friend Mauro Picone
, who was also a friend of Caccioppoli
, which he met in 1953 for the first time: Caccioppoli
expressed a profund appreciation of his work, starting a friendship with De Giorgi
. The same year he published his first paper on the topic i.e. : however, this paper and the closely following one did not attracted much interest from the mathematical community. It was only with the paper , reviewed by Laurence Chisholm Young
in the Mathematical Reviews
, that his approach to sets of finite perimeter became widely known and appreciated: also, in the review, Young
revised his previous criticism on the work of Caccioppoli
.
The last paper of De Giorgi
on the theory of perimeter
s was published in 1958: in 1959, after the death of Caccioppoli
, he started to call sets of finite perimeter "Caccioppoli sets". Two years later Herbert Federer
and Wendell Fleming published their paper , changing the approach to the theory. Basically they introduced two new kind of currents
, respectively normal currents and integral currents: in a subsequent series of papers and in the famous treatise Federer
showed that Caccioppoli sets are normal currents
of dimension in
in  -dimensional euclidean space
-dimensional euclidean space
s. However, even if the theory of Caccioppoli sets can be studied within the theory of currents
, it is customary to study it through the "traditional" approach using functions of bounded variation
, as the various sections found in a lot of important monographs in mathematics
and mathematical physics
testify (see the "References" section).
in the -dimensional setting will be used.
-dimensional setting will be used.
 be an open subset of
be an open subset of 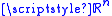 and let
and let  be a Borel set
be a Borel set
. The perimeter
of in
in  is defined as follows
is defined as follows
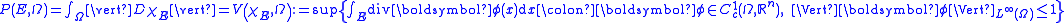
where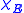 is the characteristic function of
is the characteristic function of  . If
. If 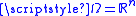 , then
, then 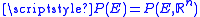 : as one can see from this definition, the perimeter
: as one can see from this definition, the perimeter
of a general Borel set
is the total variation
of its characteristic function.
Definition 2. The Borel set
 is a Caccioppoli set if and only if for every bounded
is a Caccioppoli set if and only if for every bounded
open subset of
of 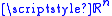 it has a locally finite
it has a locally finite
perimeter, i.e.
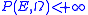
Therefore a Caccioppoli set has a characteristic function whose total variation
is locally bounded: from the theory of functions of bounded variation
it is known that this implies the existence of a vector Radon measure
 such that
such that

As noted for the case of general functions of bounded variation
, this vector measure
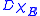 is the distributional or weak
is the distributional or weak
gradient
of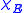 .
.
introduced the following smoothing operator, analogous to the Weierstrass transform
in the one-dimensional case
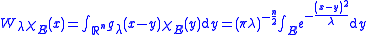
As one can esily prove,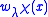 is a smooth function
is a smooth function
for all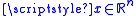 , such that
, such that
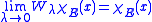
also, its gradient
is everywhere well defined, and so is its absolute value
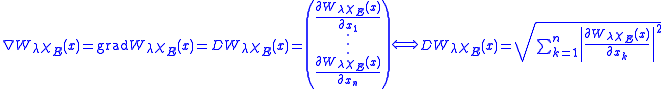
Having defined this function, De Giorgi gives the following definition of perimeter
:
Definition 3. et be an open subset of
be an open subset of  and let
and let  be a Borel set
be a Borel set
. The perimeter
of in
in  is the value
is the value
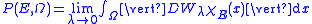
Actually De Giorgi considered the case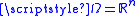 : however, the extension to the general case is not difficult. It can be proved that the two definitions are exactly equivalent: for a proof see the already cited De Giorgi's papers or the book . Now having defined what a perimeter is, De Giorgi gives the same definition 2 of what a set of (locally) finite
: however, the extension to the general case is not difficult. It can be proved that the two definitions are exactly equivalent: for a proof see the already cited De Giorgi's papers or the book . Now having defined what a perimeter is, De Giorgi gives the same definition 2 of what a set of (locally) finite
perimeter is.
is supposed to have:
) of the (vector) Radon measure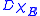 is a subset
is a subset
of the boundary
of ,
, 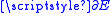 . To see this choose
. To see this choose 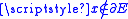 : then
: then  belongs to the open set
belongs to the open set
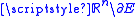 and this implies that it belongs to an open neighborhood
and this implies that it belongs to an open neighborhood  contained in the interior
contained in the interior
of or in the interior of
or in the interior of 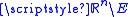 . If
. If 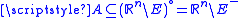 where
where 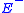 is the closure
is the closure
of , then
, then 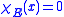 on
on  and
and
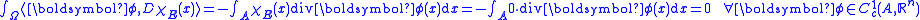
thus does not belong to the support
does not belong to the support 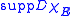 . Otherwise, if
. Otherwise, if 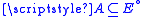 then
then
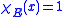 on
on  so
so

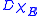 and from the properties of the perimeter, the following formula holds true:
and from the properties of the perimeter, the following formula holds true:
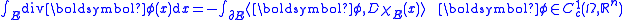
As it is easily seen, this is a version of the divergence theorem
for domains with non smooth boundary
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Caccioppoli set is a set whose boundary
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
is measurable and has a (at least locally
Local property
In mathematics, a phenomenon is sometimes said to occur locally if, roughly speaking, it occurs on sufficiently small or arbitrarily small neighborhoods of points.-Properties of a single space:...
) finite measure
Measure
- Legal :* Measure of the Church of England is a law passed by the General Synod and the UK Parliament equivalent of an Act* Measure of the National Assembly for Wales, a law specific to Wales passed by the Welsh Assembly between 2007 and 2011...
. A synonym is set of (locally
Local property
In mathematics, a phenomenon is sometimes said to occur locally if, roughly speaking, it occurs on sufficiently small or arbitrarily small neighborhoods of points.-Properties of a single space:...
) finite perimeter. Basically, a set is a Caccioppoli set if its characteristic function is a function of bounded variation.
History
The basic concept of a Caccioppoli set was firstly introduced by the Italian mathematician Renato CaccioppoliRenato Caccioppoli
Renato Caccioppoli was an Italian mathematician.- Biography :Born in Naples, Campania, he was the son of Giuseppe Caccioppoli , a surgeon, and his second wife Sofia Bakunin , daughter of the Russian revolutionary Mikhail Bakunin. After earning his diploma in 1921, he enrolled in the department of...
in the paper : considering a plane set or a surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
defined on a open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
in the plane
Plane (mathematics)
In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...
, he defined their measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
or area as the total variation
Total variation
In mathematics, the total variation identifies several slightly different concepts, related to the structure of the codomain of a function or a measure...
in the sense of Tonelli
Leonida Tonelli
Leonida Tonelli was an Italian mathematician, most noted for creating Tonelli's theorem, usually considered a forerunner to Fubini's theorem.-External links:...
of their defining functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
, i.e. of their parametric equations, provided this quantity was bounded. The measure of the boundary of a set
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
was defined as a functional
Functional (mathematics)
In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...
, precisely a set function
Set function
In mathematics, a set function is a function whose input is a set. The output is usually a number. Often the input is a set of real numbers, a set of points in Euclidean space, or a set of points in some measure space.- Examples :...
, for the first time: also, being defined on open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
s, it can be defined on all Borel set
Borel set
In mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...
s and its value can be approximated by the values it takes on an increasing net
Net (mathematics)
In mathematics, more specifically in general topology and related branches, a net or Moore–Smith sequence is a generalization of the notion of a sequence. In essence, a sequence is a function with domain the natural numbers, and in the context of topology, the range of this function is...
of subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s. Another clearly stated (and demonstrated) property of this functional was its lower semi-continuity
Semi-continuity
In mathematical analysis, semi-continuity is a property of extended real-valued functions that is weaker than continuity...
.
In the paper , he made the concept precise by using a triangular mesh
Polygon mesh
A polygon mesh or unstructured grid is a collection of vertices, edges and faces that defines the shape of a polyhedral object in 3D computer graphics and solid modeling...
as an increasing net
Net (mathematics)
In mathematics, more specifically in general topology and related branches, a net or Moore–Smith sequence is a generalization of the notion of a sequence. In essence, a sequence is a function with domain the natural numbers, and in the context of topology, the range of this function is...
approximating the open domain, defining positive and negative variations whose sum is the total variation, i.e. the area functional. His inspiring point of view, as he explicitly admitted, was those of Giuseppe Peano
Giuseppe Peano
Giuseppe Peano was an Italian mathematician, whose work was of philosophical value. The author of over 200 books and papers, he was a founder of mathematical logic and set theory, to which he contributed much notation. The standard axiomatization of the natural numbers is named the Peano axioms in...
, as expressed by the Peano-Jordan Measure
Jordan measure
In mathematics, the Peano–Jordan measure is an extension of the notion of size to shapes more complicated than, for example, a triangle, disk, or parallelepiped....
: associate to every portion of a surface an oriented
Orientation (mathematics)
In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...
plane area in a similar way as an approximating chord
Chord (geometry)
A chord of a circle is a geometric line segment whose endpoints both lie on the circumference of the circle.A secant or a secant line is the line extension of a chord. More generally, a chord is a line segment joining two points on any curve, such as but not limited to an ellipse...
is associated to a curve. Also, another theme found in this theory was the extension of a functional
Functional (mathematics)
In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...
from a subspace
Subspace
-In mathematics:* Euclidean subspace, in linear algebra, a set of vectors in n-dimensional Euclidean space that is closed under addition and scalar multiplication...
to the whole ambient space: the use of theorems generalizing the Hahn–Banach theorem
Hahn–Banach theorem
In mathematics, the Hahn–Banach theorem is a central tool in functional analysis. It allows the extension of bounded linear functionals defined on a subspace of some vector space to the whole space, and it also shows that there are "enough" continuous linear functionals defined on every normed...
is frequently encountered in Caccioppoli
Renato Caccioppoli
Renato Caccioppoli was an Italian mathematician.- Biography :Born in Naples, Campania, he was the son of Giuseppe Caccioppoli , a surgeon, and his second wife Sofia Bakunin , daughter of the Russian revolutionary Mikhail Bakunin. After earning his diploma in 1921, he enrolled in the department of...
research. However, the restricted meaning of total variation
Total variation
In mathematics, the total variation identifies several slightly different concepts, related to the structure of the codomain of a function or a measure...
in the sense of Tonelli
Leonida Tonelli
Leonida Tonelli was an Italian mathematician, most noted for creating Tonelli's theorem, usually considered a forerunner to Fubini's theorem.-External links:...
added much complication to the formal development of the theory, and the use of a parametric description of the sets restricted its scope.
Lamberto Cesari
Lamberto Cesari
Lamberto Cesari was an Italian mathematician naturalized in the United States.- Biography :...
introduced the "right" generalization of functions of bounded variation
Bounded variation
In mathematical analysis, a function of bounded variation, also known as a BV function, is a real-valued function whose total variation is bounded : the graph of a function having this property is well behaved in a precise sense...
to the case of several variables only in 1936: maybe this was one of the reasons that induced Caccioppoli
Renato Caccioppoli
Renato Caccioppoli was an Italian mathematician.- Biography :Born in Naples, Campania, he was the son of Giuseppe Caccioppoli , a surgeon, and his second wife Sofia Bakunin , daughter of the Russian revolutionary Mikhail Bakunin. After earning his diploma in 1921, he enrolled in the department of...
to present an improved version of his theory only nearly 24 years later, in the talk at the IV UMI
Italian Mathematical Union
The Italian Mathematical Union is a mathematics society based in Italy. It was founded on December 7, 1922 by Luigi Bianchi, Vito Volterra, and most notably, Salvatore Pincherle, who became the Union's first President...
Congress in October 1951, followed by five notes published in the Rendiconti of the Accademia Nazionale dei Lincei. These notes were sharply criticized by Laurence Chisholm Young
Laurence Chisholm Young
Laurence Chisholm Young was a mathematician known for his contributions to measure theory, the calculus of variations, optimal control theory, and potential theory...
in the Mathematical Reviews
Mathematical Reviews
Mathematical Reviews is a journal and online database published by the American Mathematical Society that contains brief synopses of many articles in mathematics, statistics and theoretical computer science.- Reviews :...
.
In 1952 Ennio de Giorgi
Ennio de Giorgi
-References:. The first paper about SBV functions and related variational problems.. The first note published by De Giorgi describing his approach to Caccioppoli sets.. The first complete exposition by De Giorgi of the theory of Caccioppoli sets.. An advanced text, oriented to the theory of minimal...
presented to the Salzburg
Salzburg
-Population development:In 1935, the population significantly increased when Salzburg absorbed adjacent municipalities. After World War II, numerous refugees found a new home in the city. New residential space was created for American soldiers of the postwar Occupation, and could be used for...
Congress of the Austrian Mathematical Society his first results related to the ideas of Caccioppoli about the definition of the measure of boundaries of sets: he obtained his results by using a smoothing operator analogous to a mollifier
Mollifier
In mathematics, mollifiers are smooth functions with special properties, used in distribution theory to create sequences of smooth functions approximating nonsmooth functions, via convolution...
, constructed from the Gaussian function, proving some results of Caccioppoli
Renato Caccioppoli
Renato Caccioppoli was an Italian mathematician.- Biography :Born in Naples, Campania, he was the son of Giuseppe Caccioppoli , a surgeon, and his second wife Sofia Bakunin , daughter of the Russian revolutionary Mikhail Bakunin. After earning his diploma in 1921, he enrolled in the department of...
in a different way. Probably he was led to study this theory by his teacher and friend Mauro Picone
Mauro Picone
Mauro Picone was an Italian mathematician. He is known for the Picone identity, for the Sturm-Picone comparison theorem and for being the founder of the Istituto Nazionale per le Applicazioni del Calcolo, presently named after him...
, who was also a friend of Caccioppoli
Renato Caccioppoli
Renato Caccioppoli was an Italian mathematician.- Biography :Born in Naples, Campania, he was the son of Giuseppe Caccioppoli , a surgeon, and his second wife Sofia Bakunin , daughter of the Russian revolutionary Mikhail Bakunin. After earning his diploma in 1921, he enrolled in the department of...
, which he met in 1953 for the first time: Caccioppoli
Renato Caccioppoli
Renato Caccioppoli was an Italian mathematician.- Biography :Born in Naples, Campania, he was the son of Giuseppe Caccioppoli , a surgeon, and his second wife Sofia Bakunin , daughter of the Russian revolutionary Mikhail Bakunin. After earning his diploma in 1921, he enrolled in the department of...
expressed a profund appreciation of his work, starting a friendship with De Giorgi
Ennio de Giorgi
-References:. The first paper about SBV functions and related variational problems.. The first note published by De Giorgi describing his approach to Caccioppoli sets.. The first complete exposition by De Giorgi of the theory of Caccioppoli sets.. An advanced text, oriented to the theory of minimal...
. The same year he published his first paper on the topic i.e. : however, this paper and the closely following one did not attracted much interest from the mathematical community. It was only with the paper , reviewed by Laurence Chisholm Young
Laurence Chisholm Young
Laurence Chisholm Young was a mathematician known for his contributions to measure theory, the calculus of variations, optimal control theory, and potential theory...
in the Mathematical Reviews
Mathematical Reviews
Mathematical Reviews is a journal and online database published by the American Mathematical Society that contains brief synopses of many articles in mathematics, statistics and theoretical computer science.- Reviews :...
, that his approach to sets of finite perimeter became widely known and appreciated: also, in the review, Young
Laurence Chisholm Young
Laurence Chisholm Young was a mathematician known for his contributions to measure theory, the calculus of variations, optimal control theory, and potential theory...
revised his previous criticism on the work of Caccioppoli
Renato Caccioppoli
Renato Caccioppoli was an Italian mathematician.- Biography :Born in Naples, Campania, he was the son of Giuseppe Caccioppoli , a surgeon, and his second wife Sofia Bakunin , daughter of the Russian revolutionary Mikhail Bakunin. After earning his diploma in 1921, he enrolled in the department of...
.
The last paper of De Giorgi
Ennio de Giorgi
-References:. The first paper about SBV functions and related variational problems.. The first note published by De Giorgi describing his approach to Caccioppoli sets.. The first complete exposition by De Giorgi of the theory of Caccioppoli sets.. An advanced text, oriented to the theory of minimal...
on the theory of perimeter
Perimeter
A perimeter is a path that surrounds an area. The word comes from the Greek peri and meter . The term may be used either for the path or its length - it can be thought of as the length of the outline of a shape. The perimeter of a circular area is called circumference.- Practical uses :Calculating...
s was published in 1958: in 1959, after the death of Caccioppoli
Renato Caccioppoli
Renato Caccioppoli was an Italian mathematician.- Biography :Born in Naples, Campania, he was the son of Giuseppe Caccioppoli , a surgeon, and his second wife Sofia Bakunin , daughter of the Russian revolutionary Mikhail Bakunin. After earning his diploma in 1921, he enrolled in the department of...
, he started to call sets of finite perimeter "Caccioppoli sets". Two years later Herbert Federer
Herbert Federer
Herbert Federer was an American mathematician. He is one of the creators of geometric measure theory, at the meeting point of differential geometry and mathematical analysis.-Career:...
and Wendell Fleming published their paper , changing the approach to the theory. Basically they introduced two new kind of currents
Current (mathematics)
In mathematics, more particularly in functional analysis, differential topology, and geometric measure theory, a k-current in the sense of Georges de Rham is a functional on the space of compactly supported differential k-forms, on a smooth manifold M. Formally currents behave like Schwartz...
, respectively normal currents and integral currents: in a subsequent series of papers and in the famous treatise Federer
Herbert Federer
Herbert Federer was an American mathematician. He is one of the creators of geometric measure theory, at the meeting point of differential geometry and mathematical analysis.-Career:...
showed that Caccioppoli sets are normal currents
Current (mathematics)
In mathematics, more particularly in functional analysis, differential topology, and geometric measure theory, a k-current in the sense of Georges de Rham is a functional on the space of compactly supported differential k-forms, on a smooth manifold M. Formally currents behave like Schwartz...
of dimension
 in
in  -dimensional euclidean space
-dimensional euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
s. However, even if the theory of Caccioppoli sets can be studied within the theory of currents
Current (mathematics)
In mathematics, more particularly in functional analysis, differential topology, and geometric measure theory, a k-current in the sense of Georges de Rham is a functional on the space of compactly supported differential k-forms, on a smooth manifold M. Formally currents behave like Schwartz...
, it is customary to study it through the "traditional" approach using functions of bounded variation
Bounded variation
In mathematical analysis, a function of bounded variation, also known as a BV function, is a real-valued function whose total variation is bounded : the graph of a function having this property is well behaved in a precise sense...
, as the various sections found in a lot of important monographs in mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and mathematical physics
Mathematical physics
Mathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...
testify (see the "References" section).
Formal definition
In what follows, the definition and properties of functions of bounded variationBounded variation
In mathematical analysis, a function of bounded variation, also known as a BV function, is a real-valued function whose total variation is bounded : the graph of a function having this property is well behaved in a precise sense...
in the
 -dimensional setting will be used.
-dimensional setting will be used.Caccioppoli definition
Definition 1. Let be an open subset of
be an open subset of 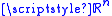 and let
and let  be a Borel set
be a Borel setBorel set
In mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...
. The perimeter
Perimeter
A perimeter is a path that surrounds an area. The word comes from the Greek peri and meter . The term may be used either for the path or its length - it can be thought of as the length of the outline of a shape. The perimeter of a circular area is called circumference.- Practical uses :Calculating...
of
 in
in  is defined as follows
is defined as follows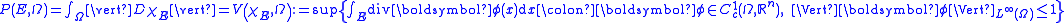
where
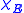 is the characteristic function of
is the characteristic function of  . If
. If 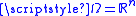 , then
, then 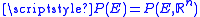 : as one can see from this definition, the perimeter
: as one can see from this definition, the perimeterPerimeter
A perimeter is a path that surrounds an area. The word comes from the Greek peri and meter . The term may be used either for the path or its length - it can be thought of as the length of the outline of a shape. The perimeter of a circular area is called circumference.- Practical uses :Calculating...
of a general Borel set
Borel set
In mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...
is the total variation
Total variation
In mathematics, the total variation identifies several slightly different concepts, related to the structure of the codomain of a function or a measure...
of its characteristic function.
Definition 2. The Borel set
Borel set
In mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...
 is a Caccioppoli set if and only if for every bounded
is a Caccioppoli set if and only if for every boundedBounded set
In mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...
open subset
 of
of 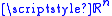 it has a locally finite
it has a locally finiteLocal property
In mathematics, a phenomenon is sometimes said to occur locally if, roughly speaking, it occurs on sufficiently small or arbitrarily small neighborhoods of points.-Properties of a single space:...
perimeter, i.e.
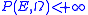
Therefore a Caccioppoli set has a characteristic function whose total variation
Total variation
In mathematics, the total variation identifies several slightly different concepts, related to the structure of the codomain of a function or a measure...
is locally bounded: from the theory of functions of bounded variation
Bounded variation
In mathematical analysis, a function of bounded variation, also known as a BV function, is a real-valued function whose total variation is bounded : the graph of a function having this property is well behaved in a precise sense...
it is known that this implies the existence of a vector Radon measure
Radon measure
In mathematics , a Radon measure, named after Johann Radon, is a measure on the σ-algebra of Borel sets of a Hausdorff topological space X that is locally finite and inner regular.-Motivation:...
 such that
such that
As noted for the case of general functions of bounded variation
Bounded variation
In mathematical analysis, a function of bounded variation, also known as a BV function, is a real-valued function whose total variation is bounded : the graph of a function having this property is well behaved in a precise sense...
, this vector measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
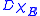 is the distributional or weak
is the distributional or weakWeak derivative
In mathematics, a weak derivative is a generalization of the concept of the derivative of a function for functions not assumed differentiable, but only integrable, i.e. to lie in the Lebesgue space L^1. See distributions for an even more general definition.- Definition :Let u be a function in the...
gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
of
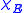 .
.De Giorgi definition
In his papers and , Ennio de GiorgiEnnio de Giorgi
-References:. The first paper about SBV functions and related variational problems.. The first note published by De Giorgi describing his approach to Caccioppoli sets.. The first complete exposition by De Giorgi of the theory of Caccioppoli sets.. An advanced text, oriented to the theory of minimal...
introduced the following smoothing operator, analogous to the Weierstrass transform
Weierstrass transform
In mathematics, the Weierstrass transform of a function f : R → R, named after Karl Weierstrass, is the function F defined by...
in the one-dimensional case
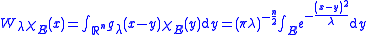
As one can esily prove,
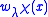 is a smooth function
is a smooth functionSmooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
for all
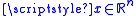 , such that
, such that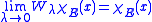
also, its gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
is everywhere well defined, and so is its absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
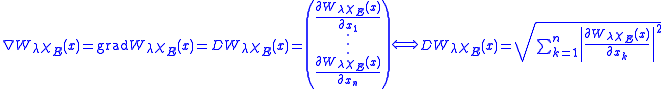
Having defined this function, De Giorgi gives the following definition of perimeter
Perimeter
A perimeter is a path that surrounds an area. The word comes from the Greek peri and meter . The term may be used either for the path or its length - it can be thought of as the length of the outline of a shape. The perimeter of a circular area is called circumference.- Practical uses :Calculating...
:
Definition 3. et
 be an open subset of
be an open subset of 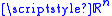 and let
and let  be a Borel set
be a Borel setBorel set
In mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...
. The perimeter
Perimeter
A perimeter is a path that surrounds an area. The word comes from the Greek peri and meter . The term may be used either for the path or its length - it can be thought of as the length of the outline of a shape. The perimeter of a circular area is called circumference.- Practical uses :Calculating...
of
 in
in  is the value
is the value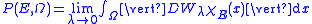
Actually De Giorgi considered the case
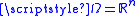 : however, the extension to the general case is not difficult. It can be proved that the two definitions are exactly equivalent: for a proof see the already cited De Giorgi's papers or the book . Now having defined what a perimeter is, De Giorgi gives the same definition 2 of what a set of (locally) finite
: however, the extension to the general case is not difficult. It can be proved that the two definitions are exactly equivalent: for a proof see the already cited De Giorgi's papers or the book . Now having defined what a perimeter is, De Giorgi gives the same definition 2 of what a set of (locally) finiteLocal property
In mathematics, a phenomenon is sometimes said to occur locally if, roughly speaking, it occurs on sufficiently small or arbitrarily small neighborhoods of points.-Properties of a single space:...
perimeter is.
Basic properties
The following properties are the ordinary properties which the general notion of a perimeterPerimeter
A perimeter is a path that surrounds an area. The word comes from the Greek peri and meter . The term may be used either for the path or its length - it can be thought of as the length of the outline of a shape. The perimeter of a circular area is called circumference.- Practical uses :Calculating...
is supposed to have:
- If
 then
then 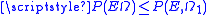 , with equality holding if and only if the closureClosure (topology)In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
, with equality holding if and only if the closureClosure (topology)In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
of is a compact subset of
is a compact subset of 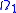 .
. 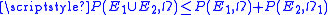 with equality holding if and only if
with equality holding if and only if 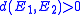 , where
, where 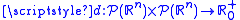 is the distance between sets in euclidean spaceEuclidean spaceIn mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
is the distance between sets in euclidean spaceEuclidean spaceIn mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
.- If the Lebesgue measureLebesgue measureIn measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
of is
is  , then
, then 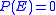 : this implies that if the symmetric differenceSymmetric differenceIn mathematics, the symmetric difference of two sets is the set of elements which are in either of the sets and not in their intersection. The symmetric difference of the sets A and B is commonly denoted by A\,\Delta\,B\,orA \ominus B....
: this implies that if the symmetric differenceSymmetric differenceIn mathematics, the symmetric difference of two sets is the set of elements which are in either of the sets and not in their intersection. The symmetric difference of the sets A and B is commonly denoted by A\,\Delta\,B\,orA \ominus B....
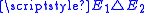 of two sets has zero Lebesgue measure, the two sets have the same perimeter i.e.
of two sets has zero Lebesgue measure, the two sets have the same perimeter i.e. 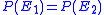 .
.
Support of the perimeter
Lemma 1. The support (in the sense of distributionsDistribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
) of the (vector) Radon measure
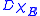 is a subset
is a subsetSubset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of the boundary
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
of
 ,
, 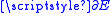 . To see this choose
. To see this choose 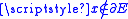 : then
: then  belongs to the open set
belongs to the open setOpen set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
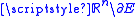 and this implies that it belongs to an open neighborhood
and this implies that it belongs to an open neighborhood  contained in the interior
contained in the interiorInterior (topology)
In mathematics, specifically in topology, the interior of a set S of points of a topological space consists of all points of S that do not belong to the boundary of S. A point that is in the interior of S is an interior point of S....
of
 or in the interior of
or in the interior of 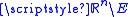 . If
. If 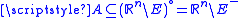 where
where 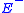 is the closure
is the closureClosure (topology)
In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
of
 , then
, then 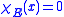 on
on  and
and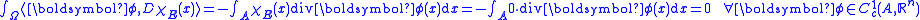
thus
 does not belong to the support
does not belong to the support 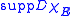 . Otherwise, if
. Otherwise, if 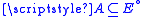 then
then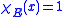 on
on  so
so
A Gauss–Green formula
From the definition of the vector Radon measureRadon measure
In mathematics , a Radon measure, named after Johann Radon, is a measure on the σ-algebra of Borel sets of a Hausdorff topological space X that is locally finite and inner regular.-Motivation:...
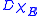 and from the properties of the perimeter, the following formula holds true:
and from the properties of the perimeter, the following formula holds true: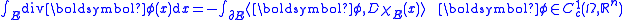
As it is easily seen, this is a version of the divergence theorem
Divergence theorem
In vector calculus, the divergence theorem, also known as Gauss' theorem , Ostrogradsky's theorem , or Gauss–Ostrogradsky theorem is a result that relates the flow of a vector field through a surface to the behavior of the vector field inside the surface.More precisely, the divergence theorem...
for domains with non smooth boundary
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
.

