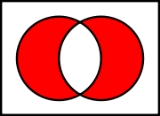
Symmetric difference
Encyclopedia
 |
| Venn diagram Venn diagram Venn diagrams or set diagrams are diagrams that show all possible logical relations between a finite collection of sets . Venn diagrams were conceived around 1880 by John Venn... of  The symmetric difference is the union Union (set theory) In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :... without the intersection Intersection (set theory) In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements.... : 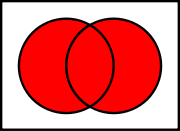  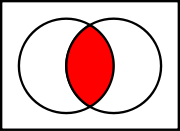   |
In mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the symmetric difference of two sets is the set of elements which are in either of the sets and not in their intersection. The symmetric difference of the sets A and B is commonly denoted by
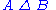
or
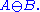
For example, the symmetric difference of the sets {1,2,3} and {3,4} is {1,2,4}. The symmetric difference of the set of all students and the set of all females consists of all male students together with all female non-students.
The power set of any set becomes an abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
under the operation of symmetric difference, with the empty set
Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
as the neutral element of the group and every element in this group being its own inverse
Inverse element
In abstract algebra, the idea of an inverse element generalises the concept of a negation, in relation to addition, and a reciprocal, in relation to multiplication. The intuition is of an element that can 'undo' the effect of combination with another given element...
. The power set of any set becomes a Boolean ring
Boolean ring
In mathematics, a Boolean ring R is a ring for which x2 = x for all x in R; that is, R consists only of idempotent elements....
with symmetric difference as the addition of the ring and intersection
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
as the multiplication of the ring.
Properties
Venn diagram of 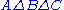   |
The symmetric difference is equivalent to the union
Union (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
of both relative complement
Complement (set theory)
In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
s, that is:
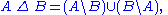
and it can also be expressed as the union of the two sets, minus their intersection
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
:
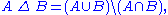
or with the XOR operation:
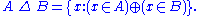
The symmetric difference is commutative
Commutativity
In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
and associative
Associativity
In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
:
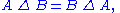
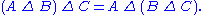
Thus, the repeated symmetric difference is an operation on a multiset
Multiset
In mathematics, the notion of multiset is a generalization of the notion of set in which members are allowed to appear more than once...
of sets giving the set of elements which are in an odd number of sets.
The symmetric difference of two repeated symmetric differences is the repeated symmetric difference of the join of the two multisets, where for each double set both can be removed. In particular:

This implies a sort of triangle inequality
Triangle inequality
In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....
: the symmetric difference of A and C is contained in the union of the symmetric difference of A and B and that of B and C. (But note that for the diameter
Diameter
In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints are on the circle. The diameters are the longest chords of the circle...
of the symmetric difference the triangle inequality does not hold.)
The empty set
Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
is neutral
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
, and every set is its own inverse:


Taken together, we see that the power set of any set X becomes an abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
if we use the symmetric difference as operation. Because every element in this group is its own inverse, this is in fact a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over the field with 2 elements
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
Z2. If X is finite, then the singletons form a basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
of this vector space, and its dimension is therefore equal to the number of elements of X. This construction is used in graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, to define the cycle space
Cycle space
In graph theory, an area of mathematics, a cycle space is a vector space defined from an undirected graph; elements of the cycle space represent formal combinations of cycles in the graph....
of a graph.
Intersection distributes
Distributivity
In mathematics, and in particular in abstract algebra, distributivity is a property of binary operations that generalizes the distributive law from elementary algebra.For example:...
over symmetric difference:
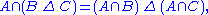
and this shows that the power set of X becomes a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
with symmetric difference as addition and intersection as multiplication. This is the prototypical example of a Boolean ring
Boolean ring
In mathematics, a Boolean ring R is a ring for which x2 = x for all x in R; that is, R consists only of idempotent elements....
.
The symmetric difference can be defined in any Boolean algebra, by writing
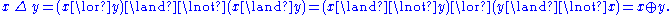
This operation has the same properties as the symmetric difference of sets.
n-ary symmetric difference
As above, the symmetric difference of a collection of sets contains just elements which are in an odd number of the sets in the collection: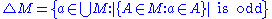 .
.Evidently, this is well-defined only when each element of the union
 is contributed by a finite number of elements of
is contributed by a finite number of elements of  .
.Symmetric difference on measure spaces
As long as there is a notion of "how big" a set is, the symmetric difference between two sets can be considered a measure of how "far apart" they are. Formally, if μ is a σ-finite measure defined on a σ-algebraSigma-algebra
In mathematics, a σ-algebra is a technical concept for a collection of sets satisfying certain properties. The main use of σ-algebras is in the definition of measures; specifically, the collection of sets over which a measure is defined is a σ-algebra...
Σ, the function,
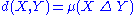
is a pseudometric
Pseudometric space
In mathematics, a pseudometric space is a generalized metric space in which the distance between two distinct points can be zero. In the same way as every normed space is a metric space, every seminormed space is a pseudometric space...
on Σ. d becomes a metric
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
if Σ is considered modulo the equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
X ~ Y if and only if
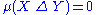 . The resulting metric space is separable if and only if L2(μ) is separable.
. The resulting metric space is separable if and only if L2(μ) is separable.See also
- Algebra of setsAlgebra of setsThe algebra of sets develops and describes the basic properties and laws of sets, the set-theoretic operations of union, intersection, and complementation and the relations of set equality and set inclusion...
- Boolean function
- Difference (set theory)
- Exclusive or
- Fuzzy setFuzzy setFuzzy sets are sets whose elements have degrees of membership. Fuzzy sets were introduced simultaneously by Lotfi A. Zadeh and Dieter Klaua in 1965 as an extension of the classical notion of set. In classical set theory, the membership of elements in a set is assessed in binary terms according to...
- Logical graphLogical graphA logical graph is a special type of diagramatic structure in any one of several systems of graphical syntax that Charles Sanders Peirce developed for logic....
- Minimal negation operator
- Set theorySet theorySet theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
- SymmetrySymmetrySymmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...

