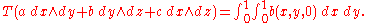Current (mathematics)
Encyclopedia
In mathematics
, more particularly in functional analysis
, differential topology
, and geometric measure theory
, a k-current in the sense of Georges de Rham
is a functional
on the space of compactly supported differential k-forms
, on a smooth manifold M. Formally currents behave like Schwartz distributions on a space of differential forms. In a geometric setting, they can represent integration over a submanifold, generalizing the Dirac delta function
, or more generally even directional derivative
s of delta functions (multipoles) spread out along subsets of M.
denote the space of smooth
m-forms with compact support on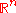
. A current is a linear functional
on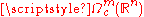
which is continuous in the sense of distribution
s. Thus a linear functional
is an m-current if it is continuous
in the following sense: If a sequence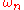
of smooth forms, all supported in the same compact set, is such that all derivatives of all their coefficients tend uniformly to 0 when 
tends to infinity, then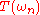 
tends to 0.
The space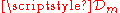
of m-dimensional currents on ℝn is a real
vector space
with operations defined by
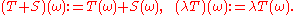
Multiplication by a constant scalar
represents a change in the multiplicity of the surface. In particular multiplication by −1 represents the change of orientation
of the surface.
Much of the theory of distributions carries over to currents with minimal adjustments. For example, one may define the support of a current T as the complement of the biggest open set
U such that T(ω) = 0 whenever the support of ω lies entirely in U.
The linear subspace
of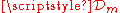
consisting of currents with compact support is denoted 
. It can be naturally identified with the dual space to the space of all smooth m-forms on ℝn.
over a compact rectifiable
oriented
submanifold M (with boundary) of dimension m defines an m-current, denoted by
:
If the boundary
∂M of M is rectifiable, then it too defines a current by integration, and one has Stokes' theorem
:
This relates the exterior derivative
d with the boundary operator ∂ on the homology
of M.
More generally, a boundary operator can be defined on arbitrary currents
by dualizing the exterior derivative
:
for all compactly supported (m−1)-forms ω.
Tk of currents, converges
to a current T if
It is possible to define several norms
on subspaces of the space of all currents. One such norm is the mass norm. If ω is an m-form, then define its comass by
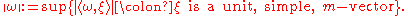
So if ω is a simple m-form, then its mass norm is the usual L∞-norm of its coefficient. The mass of a current T is then defined as
The mass of a current represents the weighted area of the generalized surface. A current such that M(T) < ∞ is representable by integration over a suitably weighted rectifiable submanifold. This is the starting point of homological integration
.
An intermediate norm is Whitney's flat norm, defined by
Two currents are close in the mass norm if they coincide away from a small part. On the other hand they are close in the flat norm if they coincide up to a small deformation.
so that the following defines a 0-current:
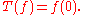
In particular every signed
regular
measure
is a 0-current:
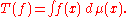
Let (x, y, z) be the coordinates in ℝ3. Then the following defines a 2-current (one of many):
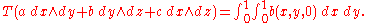
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, more particularly in functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, differential topology
Differential topology
In mathematics, differential topology is the field dealing with differentiable functions on differentiable manifolds. It is closely related to differential geometry and together they make up the geometric theory of differentiable manifolds.- Description :...
, and geometric measure theory
Geometric measure theory
In mathematics, geometric measure theory is the study of the geometric properties of the measures of sets , including such things as arc lengths and areas. It uses measure theory to generalize differential geometry to surfaces with mild singularities called rectifiable sets...
, a k-current in the sense of Georges de Rham
Georges de Rham
Georges de Rham was a Swiss mathematician, known for his contributions to differential topology.He studied at the University of Lausanne and then in Paris for a doctorate, becoming a lecturer in Lausanne in 1931; where he held positions until retirement in 1971; he held positions in Geneva in...
is a functional
Linear functional
In linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
on the space of compactly supported differential k-forms
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
, on a smooth manifold M. Formally currents behave like Schwartz distributions on a space of differential forms. In a geometric setting, they can represent integration over a submanifold, generalizing the Dirac delta function
Dirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
, or more generally even directional derivative
Directional derivative
In mathematics, the directional derivative of a multivariate differentiable function along a given vector V at a given point P intuitively represents the instantaneous rate of change of the function, moving through P in the direction of V...
s of delta functions (multipoles) spread out along subsets of M.
Definition
Let denote the space of smoothSmooth
Smooth means having a texture that lacks friction. Not rough.Smooth may also refer to:-In mathematics:* Smooth function, a function that is infinitely differentiable; used in calculus and topology...
m-forms with compact support on
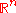. A current is a linear functionalLinear functional
In linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
on
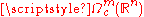which is continuous in the sense of distributionDistribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
s. Thus a linear functional
is an m-current if it is continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
in the following sense: If a sequence
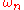of smooth forms, all supported in the same compact set, is such that all derivatives of all their coefficients tend uniformly to 0 when tends to infinity, then 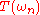tends to 0.The space
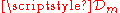of m-dimensional currents on ℝn is a realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
with operations defined by
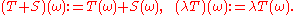
Multiplication by a constant scalar
Scalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
represents a change in the multiplicity of the surface. In particular multiplication by −1 represents the change of orientation
Orientation (geometry)
In geometry the orientation, angular position, or attitude of an object such as a line, plane or rigid body is part of the description of how it is placed in the space it is in....
of the surface.
Much of the theory of distributions carries over to currents with minimal adjustments. For example, one may define the support of a current T as the complement of the biggest open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
U such that T(ω) = 0 whenever the support of ω lies entirely in U.
The linear subspace
Linear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
of
consisting of currents with compact support is denoted . It can be naturally identified with the dual space to the space of all smooth m-forms on ℝn.Homological theory
IntegrationIntegral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
over a compact rectifiable
Rectifiable set
In mathematics, a rectifiable set is a set that is smooth in a certain measure-theoretic sense. It is an extension of the idea of a rectifiable curve to higher dimensions; loosely speaking, a rectifiable set is a rigorous formulation of a piece-wise smooth set...
oriented
Orientation (mathematics)
In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...
submanifold M (with boundary) of dimension m defines an m-current, denoted by
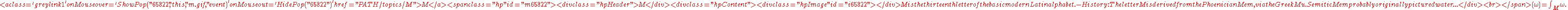
:If the boundary
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
∂M of M is rectifiable, then it too defines a current by integration, and one has Stokes' theorem
Stokes' theorem
In differential geometry, Stokes' theorem is a statement about the integration of differential forms on manifolds, which both simplifies and generalizes several theorems from vector calculus. Lord Kelvin first discovered the result and communicated it to George Stokes in July 1850...
:
This relates the exterior derivative
Exterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
d with the boundary operator ∂ on the homology
Homology (mathematics)
In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...
of M.
More generally, a boundary operator can be defined on arbitrary currents
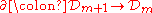
by dualizing the exterior derivative
Exterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
:
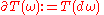
for all compactly supported (m−1)-forms ω.
Topology and norms
The space of currents is naturally endowed with the weak-* topology, which will be further simply called weak convergence. A sequenceSequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
Tk of currents, converges
Limit point
In mathematics, a limit point of a set S in a topological space X is a point x in X that can be "approximated" by points of S in the sense that every neighbourhood of x with respect to the topology on X also contains a point of S other than x itself. Note that x does not have to be an element of S...
to a current T if
It is possible to define several norms
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
on subspaces of the space of all currents. One such norm is the mass norm. If ω is an m-form, then define its comass by
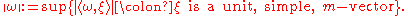
So if ω is a simple m-form, then its mass norm is the usual L∞-norm of its coefficient. The mass of a current T is then defined as
The mass of a current represents the weighted area of the generalized surface. A current such that M(T) < ∞ is representable by integration over a suitably weighted rectifiable submanifold. This is the starting point of homological integration
Homological integration
In the mathematical fields of differential geometry and geometric measure theory, homological integration or geometric integration is a method for extending the notion of the integral to manifolds...
.
An intermediate norm is Whitney's flat norm, defined by
Two currents are close in the mass norm if they coincide away from a small part. On the other hand they are close in the flat norm if they coincide up to a small deformation.
Examples
Recall thatso that the following defines a 0-current:
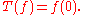
In particular every signed
Signed measure
In mathematics, signed measure is a generalization of the concept of measure by allowing it to have negative values. Some authors may call it a charge, by analogy with electric charge, which is a familiar distribution that takes on positive and negative values.-Definition:There are two slightly...
regular
Regular measure
In mathematics, a regular measure on a topological space is a measure for which every measurable set is "approximately open" and "approximately closed".-Definition:...
measure
Measure
- Legal :* Measure of the Church of England is a law passed by the General Synod and the UK Parliament equivalent of an Act* Measure of the National Assembly for Wales, a law specific to Wales passed by the Welsh Assembly between 2007 and 2011...
is a 0-current: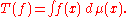Let (x, y, z) be the coordinates in ℝ3. Then the following defines a 2-current (one of many):