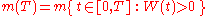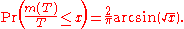Lévy arcsine law
Encyclopedia
In probability theory
, the Lévy arcsine law, found by , states that the probability distribution
of the proportion of the time that a Wiener process
(which models Brownian motion
) is positive is a random variable whose probability distribution
is the arcsine distribution. That distribution has a cumulative distribution function
proportional to arcsin(√x).
Suppose W is the standard Wiener process. For every T > 0, let
be the measure
of the set of times t between 0 and T when W(t) > 0. Then for every x ∈ [0, 1],
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, the Lévy arcsine law, found by , states that the probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
of the proportion of the time that a Wiener process
Wiener process
In mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown...
(which models Brownian motion
Brownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
) is positive is a random variable whose probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
is the arcsine distribution. That distribution has a cumulative distribution function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
proportional to arcsin(√x).
Suppose W is the standard Wiener process. For every T > 0, let
be the measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
of the set of times t between 0 and T when W(t) > 0. Then for every x ∈ [0, 1],