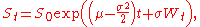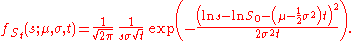Geometric Brownian motion
Encyclopedia
A geometric Brownian motion (GBM) (also known as exponential Brownian motion) is a continuous-time stochastic process
in which the logarithm
of the randomly varying quantity follows a Brownian motion
, also called a Wiener process
. It is used in mathematical finance
to model stock prices in Black–Scholes model.
(SDE):
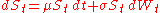
where
is a Wiener process or Brownian motion
and
('the percentage drift') and 
('the percentage volatility') are constants.
):
which is (for any value of t) a log-normally distributed random variable
with expected value
and variance
given by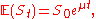
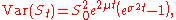
that is the probability density function
of a S_t is:
The correctness of this solution can be checked using Itō's lemma
.
When deriving further properties of GBM, use can be made of the SDE of which GBM is the solution, or the explicit solution given above can be used. For example, consider the stochastic process log(St). This is an interesting process, because in the Black–Scholes model it is related to the log return of the stock price. Using Itō's lemma with f(S) = log(S) gives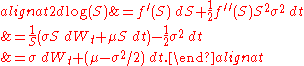
It follows that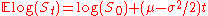
.
This result can also be derived by applying the logarithm to the explicit solution of GBM:
Taking the expectation yields the same result as above: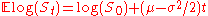
.
Some of the arguments for using GBM to model stock prices are:
However, GBM is not a completely realistic model, in particular it falls short of reality in the following points:
) is constant. If we assume that the volatility is a deterministic function of the stock price and time, this is called a local volatility
model. If instead we assume that the volatility has a randomness of its own—often described by a different equation driven by a different Brownian Motion—the model is called a stochastic volatility
model.
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
in which the logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
of the randomly varying quantity follows a Brownian motion
Brownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
, also called a Wiener process
Wiener process
In mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown...
. It is used in mathematical finance
Mathematical finance
Mathematical finance is a field of applied mathematics, concerned with financial markets. The subject has a close relationship with the discipline of financial economics, which is concerned with much of the underlying theory. Generally, mathematical finance will derive and extend the mathematical...
to model stock prices in Black–Scholes model.
Technical definition
A stochastic process St is said to follow a GBM if it satisfies the following stochastic differential equationStochastic differential equation
A stochastic differential equation is a differential equation in which one or more of the terms is a stochastic process, thus resulting in a solution which is itself a stochastic process....
(SDE):
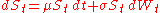
where
is a Wiener process or Brownian motionWiener process
In mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown...
and
('the percentage drift') and ('the percentage volatility') are constants.Properties of GBM
For an arbitrary initial value S0 the above SDE has the analytic solution (under Itō's interpretationIto calculus
Itō calculus, named after Kiyoshi Itō, extends the methods of calculus to stochastic processes such as Brownian motion . It has important applications in mathematical finance and stochastic differential equations....
):
which is (for any value of t) a log-normally distributed random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
with expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
and variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
given by
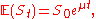
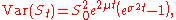
that is the probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
of a S_t is:
The correctness of this solution can be checked using Itō's lemma
Ito's lemma
In mathematics, Itō's lemma is used in Itō stochastic calculus to find the differential of a function of a particular type of stochastic process. It is named after its discoverer, Kiyoshi Itō...
.
When deriving further properties of GBM, use can be made of the SDE of which GBM is the solution, or the explicit solution given above can be used. For example, consider the stochastic process log(St). This is an interesting process, because in the Black–Scholes model it is related to the log return of the stock price. Using Itō's lemma with f(S) = log(S) gives
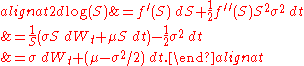
It follows that
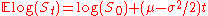.This result can also be derived by applying the logarithm to the explicit solution of GBM:
Taking the expectation yields the same result as above:
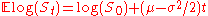.Use of GBM in finance
Geometric Brownian Motion is used to model stock prices in the Black–Scholes model and is the most widely used model of stock price behavior.Some of the arguments for using GBM to model stock prices are:
- The expected returns of GBM are independent of the value of the process (stock price), which agrees with what we would expect in reality.
- A GBM process only assumes positive values, just like real stock prices.
- A GBM process shows the same kind of 'roughness' in its paths as we see in real stock prices.
- Calculations with GBM processes are relatively easy.
However, GBM is not a completely realistic model, in particular it falls short of reality in the following points:
- In real stock prices, volatility changes over time (possibly stochasticallyStochastic volatilityStochastic volatility models are used in the field of mathematical finance to evaluate derivative securities, such as options. The name derives from the models' treatment of the underlying security's volatility as a random process, governed by state variables such as the price level of the...
), but in GBM, volatility is assumed constant. - In real stock prices, returns are usually not normally distributed (real stock returns have higher kurtosisKurtosisIn probability theory and statistics, kurtosis is any measure of the "peakedness" of the probability distribution of a real-valued random variable...
('fatter tails'), which means there is a higher chance of large price changes).
Extensions of GBM
In an attempt to make GBM more realistic as a model for stock prices, one can drop the assumption that the volatility () is constant. If we assume that the volatility is a deterministic function of the stock price and time, this is called a local volatilityLocal volatility
A local volatility model, in mathematical finance and financial engineering, is one which treats volatility as a function of the current asset level S_t and of time t .-Formulation:...
model. If instead we assume that the volatility has a randomness of its own—often described by a different equation driven by a different Brownian Motion—the model is called a stochastic volatility
Stochastic volatility
Stochastic volatility models are used in the field of mathematical finance to evaluate derivative securities, such as options. The name derives from the models' treatment of the underlying security's volatility as a random process, governed by state variables such as the price level of the...
model.