
Lévy process
Encyclopedia
In probability theory
, a Lévy process, named after the French mathematician Paul Lévy
, is any continuous-time stochastic process
that starts at 0, admits càdlàg
modification and has "stationary independent increments" — this phrase will be explained below. It is a stochastic analog of independent and identically distributed random variables
, and the most well-known examples are the Wiener process
and the Poisson process
.
 is said to be a Lévy process if,
is said to be a Lévy process if,
Xt to each point t ≥ 0 in time. In effect it is a random function of t. The increments of such a process are the differences Xs − Xt between its values at different times t < s. To call the increments of a process independent means that increments Xs − Xt and Xu − Xv are independent random variables whenever the two time intervals do not overlap and, more generally, any finite number of increments assigned to pairwise non-overlapping time intervals are mutually (not just pairwise
) independent.
of any increment Xs − Xt depends only on the length s − t of the time interval; increments with equally long time intervals are identically distributed.
In the Wiener process
, the probability distribution of Xs − Xt is normal with expected value
0 and variance
s − t.
In the (homogeneous) Poisson process
, the probability distribution of Xs − Xt is a Poisson distribution
with expected value λ(s − t), where λ > 0 is the "intensity" or "rate" of the process.
:
, the nth moment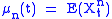 , is a polynomial function of t; these functions satisfy a binomial identity:
, is a polynomial function of t; these functions satisfy a binomial identity:
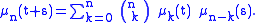
. This leads to the Lévy–Khintchine representation. If is a Lévy process, then its characteristic function satisfies the following relation:
is a Lévy process, then its characteristic function satisfies the following relation:

where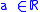 ,
,  and
and 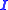 is the indicator function. The Lévy measure
is the indicator function. The Lévy measure  must be such that
must be such that
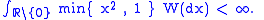
A Lévy process can be seen as having three components: a drift, a diffusion component and a jump component. These three components, and thus the Lévy–Khintchine representation of the process, are fully determined by the Lévy–Khintchine triplet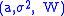 . So one can see that a purely continuous Lévy process is a Brownian motion with drift.
. So one can see that a purely continuous Lévy process is a Brownian motion with drift.
: the drift and diffusion are the absolutely continuous part, while the measure W is the singular measure.
Given a Lévy triplet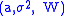 there exists three independent Lévy processes, which lie in the same probability space,
there exists three independent Lévy processes, which lie in the same probability space,  ,
, 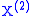 ,
, 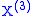 such that:
such that:
The process defined by is a Lévy process with triplet
is a Lévy process with triplet 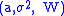 .
.
 with independent increments,
with independent increments,
where the random values occur in, say, a second countable locally compact abelian group .
.
Let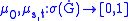 for
for 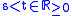
denote the (borel regular) probability measures on the initial position and the increments.
Now for let
let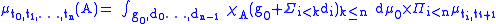 .
.
These define bona fide probability measures which, by the properties of the process,
compute appropriate probabilities for properties of paths depending on only finitely many times.
Now correspond to these measures continuous linear operators
in the obvious way. Then, for any countable set of times (for ease consider the rationals )
)
define a linear functional,
as follows. If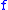 depends only on finitely many times, say
depends only on finitely many times, say 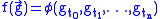
where without loss of generality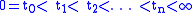 , let
, let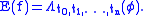
It is straightforward to see that this is well-defined and linear. Moreover it is clearly a positive, bounded operator with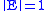 since
since  .
.
By Stone-Weierstrass, extends (uniquely) to a (linear) continuous (positive) operator (with norm 1) on its domain.
extends (uniquely) to a (linear) continuous (positive) operator (with norm 1) on its domain.
By the Riesz representation theorem
, this in turn gives rise to a (unique) (borel regular
) probability measure,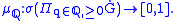
Precisely, this measure is the unique one satisfying the condition that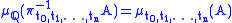
for any ,
, 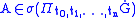 .
.
Whereas initially we knew the probability distributions of a path at given times or over time increments,
and thus could talk about local properties of the paths in the stochastic process,
the constructed measure above allows us to attach a probability distribution
to (almost) the full path space, and thus enables us to talk about global properties.
Roughly we are justified (and compelled to) thinking of the measure as though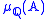
calculates "the probability" that a path occurs in (when projected onto the times
(when projected onto the times  ).
).
As an example of our new ability to talk about global properties, we have that "almost every path is left continuous",
if and only if, for every countable sequence of times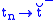 , letting
, letting 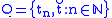 ,
,
we have that for all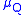 -almost-everywhere
-almost-everywhere 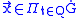 then
then  converges / converges to
converges / converges to  . This makes sense, as it can be shown that
. This makes sense, as it can be shown that
Verifying how global properties of paths over the real line can be translated into properties considering only countably many times, can be a little tricky.
There is no escaping this. Fortunately, the problem of having to change the countable set of times over which the measure is based
can be prevented. If we consider a countable dense subset, , of the reals (e.g. the rationals), we may apply knowledge of the distribution on the increments together with the stochastic measure
, of the reals (e.g. the rationals), we may apply knowledge of the distribution on the increments together with the stochastic measure 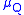 to check these global properties. For example, in the case of the Wiener process
to check these global properties. For example, in the case of the Wiener process
, we are able to check that almost every path is (i) everywhere cts; (ii) has continuity modulus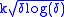 (Lévy); and thus (iii) is nowhere differentiable.
(Lévy); and thus (iii) is nowhere differentiable.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, a Lévy process, named after the French mathematician Paul Lévy
Paul Pierre Lévy
Paul Pierre Lévy was a Jewish French mathematician who was active especially in probability theory, introducing martingales and Lévy flights...
, is any continuous-time stochastic process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
that starts at 0, admits càdlàg
Càdlàg
In mathematics, a càdlàg , RCLL , or corlol function is a function defined on the real numbers that is everywhere right-continuous and has left limits everywhere...
modification and has "stationary independent increments" — this phrase will be explained below. It is a stochastic analog of independent and identically distributed random variables
Independent and identically distributed random variables
In probability theory and statistics, a sequence or other collection of random variables is independent and identically distributed if each random variable has the same probability distribution as the others and all are mutually independent....
, and the most well-known examples are the Wiener process
Wiener process
In mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown...
and the Poisson process
Poisson process
A Poisson process, named after the French mathematician Siméon-Denis Poisson , is a stochastic process in which events occur continuously and independently of one another...
.
Definition
A stochastic processStochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
 is said to be a Lévy process if,
is said to be a Lévy process if,
-
 almost surelyAlmost surelyIn probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...
almost surelyAlmost surelyIn probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory... - Independent increments: For any
 ,
, 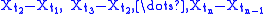 are independent
are independent - Stationary increments: For any
 ,
,  is equal in distribution to
is equal in distribution to 
-
 is almost surelyAlmost surelyIn probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...
is almost surelyAlmost surelyIn probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...
right continuous with left limitsCàdlàgIn mathematics, a càdlàg , RCLL , or corlol function is a function defined on the real numbers that is everywhere right-continuous and has left limits everywhere...
.
Independent increments
A continuous-time stochastic process assigns a random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
Xt to each point t ≥ 0 in time. In effect it is a random function of t. The increments of such a process are the differences Xs − Xt between its values at different times t < s. To call the increments of a process independent means that increments Xs − Xt and Xu − Xv are independent random variables whenever the two time intervals do not overlap and, more generally, any finite number of increments assigned to pairwise non-overlapping time intervals are mutually (not just pairwise
Pairwise independence
In probability theory, a pairwise independent collection of random variables is a set of random variables any two of which are independent. Any collection of mutually independent random variables is pairwise independent, but some pairwise independent collections are not mutually independent...
) independent.
Stationary increments
To call the increments stationary means that the probability distributionProbability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
of any increment Xs − Xt depends only on the length s − t of the time interval; increments with equally long time intervals are identically distributed.
In the Wiener process
Wiener process
In mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown...
, the probability distribution of Xs − Xt is normal with expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
0 and variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
s − t.
In the (homogeneous) Poisson process
Poisson process
A Poisson process, named after the French mathematician Siméon-Denis Poisson , is a stochastic process in which events occur continuously and independently of one another...
, the probability distribution of Xs − Xt is a Poisson distribution
Poisson distribution
In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...
with expected value λ(s − t), where λ > 0 is the "intensity" or "rate" of the process.
Divisibility
Lévy processes correspond to infinitely divisible probability distributionsInfinite divisibility (probability)
The concepts of infinite divisibility and the decomposition of distributions arise in probability and statistics in relation to seeking families of probability distributions that might be a natural choice in certain applications, in the same way that the normal distribution is...
:
- The probability distributions of the increments of any Lévy process are infinitely divisible, since the increment of length t is the sum of n increments of length t/n, which are i.i.d. by assumption (independent increments and stationarity).
- Conversely, there is a Lévy process for each infinitely divisible probability distribution: given such a distribution D, multiples and dividing define a stochastic process for positive rational time, defining it as a Dirac delta distribution for time 0 defines it for time 0, and taking limits defines it for real time. Independent increments and stationarity follow by assumption of divisibility, though one must check continuity and that taking limits gives a well-defined function for irrational time.
Moments
In any Lévy process with finite momentsMoment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
, the nth moment
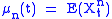 , is a polynomial function of t; these functions satisfy a binomial identity:
, is a polynomial function of t; these functions satisfy a binomial identity: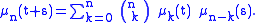
Lévy–Khintchine representation
It is possible to characterise all Lévy processes by looking at their characteristic functionCharacteristic function (probability theory)
In probability theory and statistics, the characteristic function of any random variable completely defines its probability distribution. Thus it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or cumulative...
. This leads to the Lévy–Khintchine representation. If
 is a Lévy process, then its characteristic function satisfies the following relation:
is a Lévy process, then its characteristic function satisfies the following relation:
where
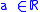 ,
,  and
and 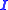 is the indicator function. The Lévy measure
is the indicator function. The Lévy measure  must be such that
must be such that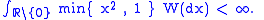
A Lévy process can be seen as having three components: a drift, a diffusion component and a jump component. These three components, and thus the Lévy–Khintchine representation of the process, are fully determined by the Lévy–Khintchine triplet
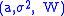 . So one can see that a purely continuous Lévy process is a Brownian motion with drift.
. So one can see that a purely continuous Lévy process is a Brownian motion with drift.Lévy–Itō decomposition
We can also construct a Lévy process from any given characteristic function of the form given in the Lévy–Khintchine representation. This expression corresponds to the decomposition of a measure in Lebesgue's decomposition theoremLebesgue's decomposition theorem
In mathematics, more precisely in measure theory, Lebesgue's decomposition theorem is a theorem which states that given \mu and \nu two σ-finite signed measures on a measurable space , there exist two σ-finite signed measures \nu_0 and \nu_1 such that:* \nu=\nu_0+\nu_1\, * \nu_0\ll\mu *...
: the drift and diffusion are the absolutely continuous part, while the measure W is the singular measure.
Given a Lévy triplet
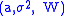 there exists three independent Lévy processes, which lie in the same probability space,
there exists three independent Lévy processes, which lie in the same probability space,  ,
, 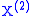 ,
, 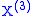 such that:
such that:
-
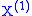 is a Brownian motionBrownian motionBrownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
is a Brownian motionBrownian motionBrownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
with drift, corresponding to the absolutely continuous part of a measure and capturing the drift a and diffusion ;
; -
 is a compound Poisson processCompound Poisson processA compound Poisson process is a continuous-time stochastic process with jumps. The jumps arrive randomly according to a Poisson process and the size of the jumps is also random, with a specified probability distribution...
is a compound Poisson processCompound Poisson processA compound Poisson process is a continuous-time stochastic process with jumps. The jumps arrive randomly according to a Poisson process and the size of the jumps is also random, with a specified probability distribution...
, corresponding to the pure point part of the singular measure W; -
 is a square integrable pure jump martingaleMartingale (probability theory)In probability theory, a martingale is a model of a fair game where no knowledge of past events can help to predict future winnings. In particular, a martingale is a sequence of random variables for which, at a particular time in the realized sequence, the expectation of the next value in the...
is a square integrable pure jump martingaleMartingale (probability theory)In probability theory, a martingale is a model of a fair game where no knowledge of past events can help to predict future winnings. In particular, a martingale is a sequence of random variables for which, at a particular time in the realized sequence, the expectation of the next value in the...
that almost surely has a countable number of jumps on a finite interval, corresponding to the singular continuous part of the singular measure W.
The process defined by
 is a Lévy process with triplet
is a Lévy process with triplet 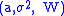 .
.Constructing a stochastic probability measure
Consider a random process; with independent increments,
with independent increments,where the random values occur in, say, a second countable locally compact abelian group
 .
.Let
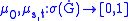 for
for 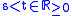
denote the (borel regular) probability measures on the initial position and the increments.
Now for
 let
let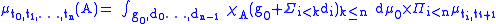 .
.These define bona fide probability measures which, by the properties of the process,
compute appropriate probabilities for properties of paths depending on only finitely many times.
Now correspond to these measures continuous linear operators

in the obvious way. Then, for any countable set of times (for ease consider the rationals
 )
)define a linear functional,

as follows. If
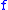 depends only on finitely many times, say
depends only on finitely many times, say 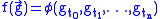
where without loss of generality
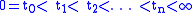 , let
, let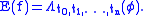
It is straightforward to see that this is well-defined and linear. Moreover it is clearly a positive, bounded operator with
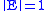 since
since  .
.By Stone-Weierstrass,
 extends (uniquely) to a (linear) continuous (positive) operator (with norm 1) on its domain.
extends (uniquely) to a (linear) continuous (positive) operator (with norm 1) on its domain.By the Riesz representation theorem
Riesz representation theorem
There are several well-known theorems in functional analysis known as the Riesz representation theorem. They are named in honour of Frigyes Riesz.- The Hilbert space representation theorem :...
, this in turn gives rise to a (unique) (borel regular
Borel regular measure
In mathematics, an outer measure μ on n-dimensional Euclidean space Rn is called Borel regular if the following two conditions hold:...
) probability measure,
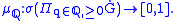
Precisely, this measure is the unique one satisfying the condition that
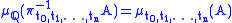
for any
 ,
, 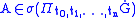 .
.Whereas initially we knew the probability distributions of a path at given times or over time increments,
and thus could talk about local properties of the paths in the stochastic process,
the constructed measure above allows us to attach a probability distribution
to (almost) the full path space, and thus enables us to talk about global properties.
Roughly we are justified (and compelled to) thinking of the measure as though
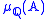
calculates "the probability" that a path occurs in
 (when projected onto the times
(when projected onto the times  ).
).As an example of our new ability to talk about global properties, we have that "almost every path is left continuous",
if and only if, for every countable sequence of times
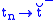 , letting
, letting 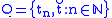 ,
,we have that for all
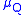 -almost-everywhere
-almost-everywhere 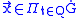 then
then  converges / converges to
converges / converges to  . This makes sense, as it can be shown that
. This makes sense, as it can be shown that
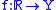 has left limits/is left cts if and only if
has left limits/is left cts if and only if 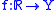 has limits/is cts under the topology on
has limits/is cts under the topology on  generated by
generated by 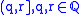 ; and
; and- if
 is second countable then
is second countable then  has limits/is cts if and only if
has limits/is cts if and only if  converges / converges to
converges / converges to 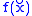 whenever
whenever 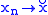 .
.
Verifying how global properties of paths over the real line can be translated into properties considering only countably many times, can be a little tricky.
There is no escaping this. Fortunately, the problem of having to change the countable set of times over which the measure is based
can be prevented. If we consider a countable dense subset,
 , of the reals (e.g. the rationals), we may apply knowledge of the distribution on the increments together with the stochastic measure
, of the reals (e.g. the rationals), we may apply knowledge of the distribution on the increments together with the stochastic measure 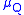 to check these global properties. For example, in the case of the Wiener process
to check these global properties. For example, in the case of the Wiener processWiener process
In mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown...
, we are able to check that almost every path is (i) everywhere cts; (ii) has continuity modulus
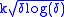 (Lévy); and thus (iii) is nowhere differentiable.
(Lévy); and thus (iii) is nowhere differentiable.See also
- Independent and identically distributed random variablesIndependent and identically distributed random variablesIn probability theory and statistics, a sequence or other collection of random variables is independent and identically distributed if each random variable has the same probability distribution as the others and all are mutually independent....

