
, a sign convention is a choice of the physical significance of sign
s (plus or minus) for a set of quantities, in a case where the choice of sign is arbitrary. "Arbitrary" here means that the same physical system can be correctly described using different choices for the signs, as long as one set of definitions is used consistently. The choices made may differ between authors. Disagreement about sign conventions is a frequent source of confusion, frustration, misunderstandings, and even outright errors. In general, a sign convention is a special case of a choice of coordinate system
for the case of one dimension.
Sometimes, the term "sign convention" is used more broadly to include factors of i
and 2π
, rather than just choices of sign.
Metric signature
In relativity, the metric signature
could either be + − − − or − + + +. A similar dual convention is used in higher-dimensional relativistic theories. The choice of signature is given a variety of names:
+ − − −:
- Timelike convention
- Particle physicsParticle physicsParticle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...
convention - West coastWest Coast of the United StatesWest Coast or Pacific Coast are terms for the westernmost coastal states of the United States. The term most often refers to the states of California, Oregon, and Washington. Although not part of the contiguous United States, Alaska and Hawaii do border the Pacific Ocean but can't be included in...
convention - Mostly minuses
- Landau-Lifshitz sign convention.
− + + +:
- Spacelike convention
- RelativityGeneral relativityGeneral relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
convention - East coastEast Coast of the United StatesThe East Coast of the United States, also known as the Eastern Seaboard, refers to the easternmost coastal states in the United States, which touch the Atlantic Ocean and stretch up to Canada. The term includes the U.S...
convention - Mostly pluses
Regarding the choice of − + + + versus + − − −, a survey of some classic textbooks reveals that Misner, Thorne and Wheeler
(MTW) chose − + + + while Weinberg chose + + + − (with the understanding that the last sign corresponds to "time"). Subsequent authors writing in particle physics have generally followed Weinberg, while authors of papers in classical gravitation and string theory
have generally followed MTW (as do most Wikipedia articles related to relativistic physics). Nevertheless, the Weinberg form is consistent with Hyperbolic quaternion
s, a forerunner of Minkowski space
.
The signature + − − − would correspond to the following metric tensor
:
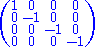
whereas the signature − + + + would correspond to this one:
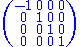
Einstein's "ex cathedra" pronouncement
While in some sense this is a mere notational convention, the choice of the signature has always engendered considerable passion and even some degree of "controversy" (not entirely serious).In an interview given on the campus of University of California, Berkeley
, Wallace Givens
(an applied mathematician
who was active in the early development of computer science) recalled an incident from his experiences as a graduate student at Princeton University
, circa 1955:
Anyway, (VeblenOswald VeblenOswald Veblen was an American mathematician, geometer and topologist, whose work found application in atomic physics and the theory of relativity. He proved the Jordan curve theorem in 1905.-Life:...
) had been trying to persuade me that in the metric for general relativity the signature of the quadratic form was quite clearly three minuses and a plus rather than three pluses and a minus, just a change in sign because it's the foundation of the concept of causality and no other signature will do for that. It really should be called a causality metric rather than a gravitational metric, but after all it was done by a physicist instead of a logician or a mathematician. Anyhow, Veblen had been trying to persuade me that it made a difference which you used, three minuses and a plus, or its negative, three pluses and a minus. Well, he was much too good a mathematician in every respect to tell me authoritatively. That was not the nature of the relationship. Veblen wasn't that kind of a person. He didn't do that to graduate students, and he didn't do it to me. But he was not without guile.
The occasion was that I was in my office waiting for the usual morning call to go into Veblen's office and talk. No one came. Veblen didn't knock, and I guess it was getting along towards lunch, so I thought I had better see what was going on. I stepped out my door and knocked on Veblen's door, and Veblen said come in and I went in. I saw what the difficulty was. He had been having a conversation with Einstein. Well, I'd met Einstein—his office was two or three doors down the hall—but I never knocked on Einstein's office because I had too much respect for his privacy and his time.
Anyway, on this occasion Veblen took the opportunity to fire a big gun on this little question of the signature. Well, both of us knew perfectly well what was going on. I don't know what the subject of the conversation with Einstein had been about. They both agreed that they were concluding it, and Einstein was about to leave. So Veblen said, "Professor Einstein, perhaps you'll decide ex cathedra a little question for us in regard to the signature of the metric." Well, Einstein laughed, quite a hearty laugh; he rumbled in laughter I think would be an appropriate way to describe it. He was flattered a little; he enjoyed it. He understood the question (and its phrasing!) and remarked quietly with some answer. This was more or less the end of the conversation and Einstein left, and I had a quiet, brief conversation with Veblen.
Now the story doesn't quite end there. Someone is supposed to ask which signature Einstein chose. Well, as a matter of fact, I don't remember, but the nature of the work at that time was of the following character. Einstein didn't give his reasons, so why did it matter which he said. That was the way things were done at Princeton in those days. Actually of course the question is easily answered by looking in Einstein's little book called Relativity, and I think it's three minuses and a plus. I think that's what he said, but I can't even be absolutely sure of that. But as I point out, I don't really think it matters very much. At least I wasn't convinced, even as a graduate student that it mattered very much.
Curvature
The Ricci tensor is defined as the contraction of the Riemann tensor. Some authors use the contraction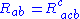 , whereas others use the alternative
, whereas others use the alternative  . Due to the symmetries of the Riemann tensor, these two definitions differ by a minus sign.
. Due to the symmetries of the Riemann tensor, these two definitions differ by a minus sign.In fact the second definition of the Ricci tensor is
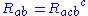 . The sign of the Ricci tensor does not change, because the two sign conventions concern the sign of the Riemann tensor. The second definition just compensates the sign and it works together with the second definition of the Riemann tensor (see e.g. Barrett O'Neill's Semi-riemannian geometry).
. The sign of the Ricci tensor does not change, because the two sign conventions concern the sign of the Riemann tensor. The second definition just compensates the sign and it works together with the second definition of the Riemann tensor (see e.g. Barrett O'Neill's Semi-riemannian geometry).Other sign conventions
- The sign choice for timeArrow of timeThe arrow of time, or time’s arrow, is a term coined in 1927 by the British astronomer Arthur Eddington to describe the "one-way direction" or "asymmetry" of time...
in frames of reference and proper time: + for future and − for past is universally accepted. - The choice of
 in the Dirac equationDirac equationThe Dirac equation is a relativistic quantum mechanical wave equation formulated by British physicist Paul Dirac in 1928. It provided a description of elementary spin-½ particles, such as electrons, consistent with both the principles of quantum mechanics and the theory of special relativity, and...
in the Dirac equationDirac equationThe Dirac equation is a relativistic quantum mechanical wave equation formulated by British physicist Paul Dirac in 1928. It provided a description of elementary spin-½ particles, such as electrons, consistent with both the principles of quantum mechanics and the theory of special relativity, and...
. - The sign of the electric chargeElectric chargeElectric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
, field strength tensorElectromagnetic tensorThe electromagnetic tensor or electromagnetic field tensor is a mathematical object that describes the electromagnetic field of a physical system in Maxwell's theory of electromagnetism...
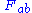 in gauge theoriesGauge theoryIn physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
in gauge theoriesGauge theoryIn physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
and classical electrodynamicsMaxwell's equationsMaxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
. - Time dependence of a positive-frequency wave (see, e.g., the electromagnetic wave equationElectromagnetic wave equationThe electromagnetic wave equation is a second-order partial differential equation that describes the propagation of electromagnetic waves through a medium or in a vacuum...
):-
 (mainly used by physicists)
(mainly used by physicists) -
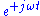 (mainly used by engineers)
(mainly used by engineers)
-
- The sign for the imaginary part of permittivity (in fact dictated by the choice of sign for time-dependence)
- The signs of distances and radii of curvatureRadius of curvature (optics)Radius of curvature has specific meaning and sign convention in optical design. A spherical lens or mirror surface has a center of curvature located in either along or decentered from the system local optical axis. The vertex of the lens surface is located on the local optical axis...
of optical surfaces in opticsOpticsOptics is the branch of physics which involves the behavior and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behavior of visible, ultraviolet, and infrared light... - The sign of work in the first law of thermodynamicsFirst law of thermodynamicsThe first law of thermodynamics is an expression of the principle of conservation of work.The law states that energy can be transformed, i.e. changed from one form to another, but cannot be created nor destroyed...
.
It is often considered good form to state explicitly which sign convention is to be used at the beginning of each book or article.

