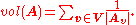Bass–Serre theory
Encyclopedia
Bass–Serre theory is a part of the mathematical
subject of group theory
that deals with analyzing the algebraic structure of groups acting
by automorphisms on simplicial trees
. The theory relates group actions on trees with decomposing groups as iterated applications of the operations of free product with amalgamation and HNN extension
, via the notion of the fundamental group of a graph of groups
.
Bass–Serre theory can be regarded as one-dimensional version of the orbifold theory
.
in 1970s and formalized in Trees, Serre's seminal 1977 monograph (developed in collaboration with Hyman Bass
) on the subject. Serre's original motivation was to understand the structure of certain algebraic group
s whose Bruhat–Tits building
s are trees. However, the theory quickly became a standard tool of geometric group theory
and geometric topology
, particularly the study of 3-manifold
s. Subsequent work of Hyman Bass
contributed substantially to the formalization and development of basic tools of the theory and currently the term "Bass–Serre theory" is widely used to describe the subject.
Mathematically, Bass–Serre theory builds on exploiting and generalizing the properties of two older group-theoretic constructions: free product with amalgamation and HNN extension
. However, unlike the traditional algebraic study of these two constructions, Bass–Serre theory uses the geometric language of covering theory and fundamental group
s. Graphs of groups, which are the basic objects of Bass–Serre theory, can be viewed as one-dimensional versions of orbifold
s.
Apart from Serre's book, the basic treatment of Bass–Serre theory is available in the article of Bass, the article of Scott and Wall and the books of Hatcher
, Baumslag
, Dicks and Dunwoody
and Cohen.
is slightly different from the standard set-up of graph theory
. Here a graph A consists of a vertex set V, an edge set E, an edge reversal map such that
such that 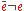 and
and  for every
for every  , and an initial vertex map
, and an initial vertex map  . Thus in A every edge e comes equipped with its formal inverse
. Thus in A every edge e comes equipped with its formal inverse 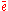 . The vertex o(e) is called the origin or the initial vertex of e and the vertex
. The vertex o(e) is called the origin or the initial vertex of e and the vertex  is called the terminus of e and is denoted t(e). Both loop-edges (that is, edges e such that o(e) = t(e)) and multiple edges are allowed. An orientation on A is a partition of E into the union of two disjoint subsets E+ and E− so that for every edge e exactly one of the edges from the pair
is called the terminus of e and is denoted t(e). Both loop-edges (that is, edges e such that o(e) = t(e)) and multiple edges are allowed. An orientation on A is a partition of E into the union of two disjoint subsets E+ and E− so that for every edge e exactly one of the edges from the pair  belongs to E+ and the other belongs to E−.
belongs to E+ and the other belongs to E−.
A consists of the following data:
For every e∈E the map is also denoted by ωe.
is also denoted by ωe.
s), and the second using the language of groupoid
s.
The algebraic definition is easier to state:
First, choose a spanning tree
T in A. The fundamental group of A with respect to T, denoted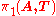 , is defined as the quotient of the free product
, is defined as the quotient of the free product
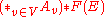
where F(E) is a free group
with free basis E, subject to the following relations:
There is also a notion of the fundamental group of A with respect to a base-vertex , denoted
, denoted 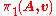 , which is defined using the formalism of groupoid
, which is defined using the formalism of groupoid
s. It turns out that for every choice of a base-vertex v and every spanning tree T in A the groups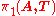 and
and 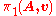 are naturally isomorphic
are naturally isomorphic
.
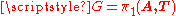 defined above admits an algebraic description in terms of iterated amalgamated free products and HNN extension
defined above admits an algebraic description in terms of iterated amalgamated free products and HNN extension
s. First, form a group B as a quotient of the free product

subject to the relations
This presentation can be rewritten as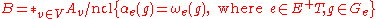
which shows that B is an iterated amalgamated free product of the vertex groups Av.
Then the group has the presentation
has the presentation
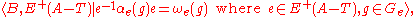
which shows that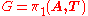 is a multiple HNN extension
is a multiple HNN extension
of B with stable letters .
.
Thus a splitting where all edge groups are finite is called a splitting over finite groups.
Algebraically, a splitting of G with trivial edge groups corresponds to a free product decomposition
where F(X) is a free group
with free basis X=E+(A-T) consisting of all positively oriented edges (with respect to some orientation on A) in the complement of some spanning tree T of A.
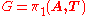 represented as a product of the form
represented as a product of the form
where e1,..., en is a closed edge-path in A with the vertex sequence v0, v1,...,vn=v0 (that is v0=o(e1), vn=t(en) and vi=t(ei)=o(ei+1) for 0 < i < n) and where for i = 0, ..., n.
for i = 0, ..., n.
Suppose that g = 1 in G. Then
The normal forms theorem immediately implies that the canonical homomorphisms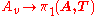 are injective, so that we can think of the vertex groups Av as subgroups of G.
are injective, so that we can think of the vertex groups Av as subgroups of G.
Higgins has given a nice version of the normal form using the fundamental groupoid
of a graph of groups. This avoids choosing a base point or tree, and has been exploited in.
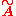 , which is a tree that comes equipped with a natural group action
, which is a tree that comes equipped with a natural group action
of the fundamental group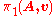 without edge-inversions.
without edge-inversions.
Moreover, the quotient graph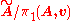 is isomorphic to A.
is isomorphic to A.
Similarly, if G is a group acting on a tree X without edge-inversions (that is, so that for every edge e of X and every g in G we have ), one can define the natural notion of a quotient graph of groups A. The underlying graph A of A is the quotient graph X/G. The vertex groups of A are isomorphic to vertex stabilizers in G of vertices of X and the edge groups of A are isomorphic to edge stabilizers in G of edges of X.
), one can define the natural notion of a quotient graph of groups A. The underlying graph A of A is the quotient graph X/G. The vertex groups of A are isomorphic to vertex stabilizers in G of vertices of X and the edge groups of A are isomorphic to edge stabilizers in G of edges of X.
Moreover, if X was the Bass–Serre covering tree of a graph of groups A and if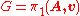 then the quotient graph of groups for the action of G on X can be chosen to be naturally isomorphic to A.
then the quotient graph of groups for the action of G on X can be chosen to be naturally isomorphic to A.
 and there is an equivariant isomorphism between the tree X and the Bass–Serre covering tree
and there is an equivariant isomorphism between the tree X and the Bass–Serre covering tree 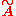 . More precisely, there is a group isomorphism
. More precisely, there is a group isomorphism
 and a graph isomorphism
and a graph isomorphism 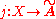 such that for every g in G, for every vertex x of X and for every edge e of X we have j(gx) = g j(x) and j(ge) = g j(e).
such that for every g in G, for every vertex x of X and for every edge e of X we have j(gx) = g j(x) and j(ge) = g j(e).
One of the immediate consequences of the above result is the classic Kurosh subgroup theorem
describing the algebraic structure of subgroups of free product
s.
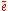 ) with two distinct end-vertices u = o(e) and v = t(e), vertex groups H=Au, K=Av, an edge group C=Ae and the boundary monomorphisms
) with two distinct end-vertices u = o(e) and v = t(e), vertex groups H=Au, K=Av, an edge group C=Ae and the boundary monomorphisms 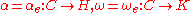 .
.
Then T = A is a spanning tree in A and the fundamental group is isomorphic to the amalgamated free product
is isomorphic to the amalgamated free product

In this case the Bass–Serre tree can be described as follows. The vertex set of X is the set of coset
can be described as follows. The vertex set of X is the set of coset
s

Two vertices gK and fH are adjacent in X whenever there exists k ∈ K such that fH = gkH (or, equivalently, whenever there is h ∈ H such that gK = fhK).
The G-stabilizer of every vertex of X of type gK is equal to gKg−1 and the G-stabilizer of every vertex of X of type gH is equal to gHg−1. For an edge [gH, ghK] of X its G-stabilizer is equal to ghα(C)h−1g−1.
For every c ∈ C and h ∈ 'k ∈ K' the edges [gH, ghK] and [gH, ghα(c)K] are equal and the degree of the vertex gH in X is equal to the index
[H:α(C)].
Similarly, every vertex of type gK has degree [K:ω(C)] in X.
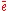 ), a single vertex v = o(e) = t(e), a vertex group B = Av, an edge group C = Ae and the boundary monomorphisms
), a single vertex v = o(e) = t(e), a vertex group B = Av, an edge group C = Ae and the boundary monomorphisms 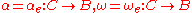 .
.
Then T = v is a spanning tree in A and the fundamental group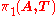 is isomorphic to the HNN extension
is isomorphic to the HNN extension
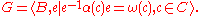
with the base group B, stable letter e and the associated subgroups H = α(C), K = ω(C) in B.
The composition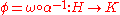 is an isomorphism and the above HNN-extension presentation of G can be rewritten as
is an isomorphism and the above HNN-extension presentation of G can be rewritten as
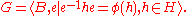
In this case the Bass–Serre tree can be described as follows. The vertex set of X is the set of coset
can be described as follows. The vertex set of X is the set of coset
s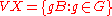 .
.
Two vertices gB and fB are adjacent in X whenever there exists such that either fB = gbeB or fB = gbe−1B. The G-stabilizer of every vertex of X is conjugate to B in G and the stabilizer of every edge of X is conjugate to H in G. Every vertex of X has degree equal to [B : H] + [B : K].
such that either fB = gbeB or fB = gbe−1B. The G-stabilizer of every vertex of X is conjugate to B in G and the stabilizer of every edge of X is conjugate to H in G. Every vertex of X has degree equal to [B : H] + [B : K].
π1(A,v) of the underlying graph A in the standard sense of algebraic topology and the Bass–Serre covering tree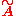 is equal to the standard universal covering space
is equal to the standard universal covering space 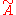 of A. Moreover, the action of π1(A,v) on
of A. Moreover, the action of π1(A,v) on 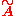 is exactly the standard action of π1(A,v) on
is exactly the standard action of π1(A,v) on 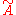 by deck transformations.
by deck transformations.
 . This is equivalent to the condition that A is a tree and that for every edge e = [u, z] of A (with o(e) = u, t(e) = z) such that u is closer to v than z we have [Az : ωe(Ae)] = 1, that is Az = ωe(Ae).
. This is equivalent to the condition that A is a tree and that for every edge e = [u, z] of A (with o(e) = u, t(e) = z) such that u is closer to v than z we have [Az : ωe(Ae)] = 1, that is Az = ωe(Ae).
An action of a group G on a tree X without edge-inversions is called trivial if there exists a vertex x of X that is fixed by G, that is such that Gx = x. It is known that an action of G on X is trivial if and only if the quotient graph of groups for that action is trivial.
Typically, only nontrivial actions on trees are studied in Bass–Serre theory since trivial graphs of groups do not carry any interesting algebraic information, although trivial actions in the above sense (e. g. actions of groups by automorphisms on rooted trees) may also be interesting for other mathematical reasons.
One of the classic and still important results of the theory is a theorem of Stallings about ends of groups. The theorem states that a finitely generated group has more than one end if and only if this group admits a nontrivial splitting over finite subroups that is, if and only if the group admits a nontrivial action without inversions on a tree with finite edge stabilizers.
An important general result of the theory states that if G is a group with Kazhdan's property (T)
then G does not admit any nontrivial splitting, that is, that any action of G on a tree X without edge-inversions has a global fixed vertex.
For every g∈G put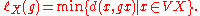
Then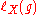 is called the translation length of g on X.
is called the translation length of g on X.
The function
is called the hyperbolic length function or the translation length function for the action of G on X.
The length-function is said to be abelian if it is a group homomorphism
is said to be abelian if it is a group homomorphism
from G to and non-abelian otherwise. Similarly, the action of G on X is said to be abelian if the associated hyperbolic length function is abelian and is said to be non-abelian otherwise.
and non-abelian otherwise. Similarly, the action of G on X is said to be abelian if the associated hyperbolic length function is abelian and is said to be non-abelian otherwise.
In general, an action of G on a tree X without edge-inversions is said to be minimal if there are no proper G-invariant subtrees in X.
An important fact in the theory says that minimal non-abelian tree actions are uniquely determined by their hyperbolic length functions:
f : X → Y which is G-equivariant, that is f(gx) = g f(x) for every g ∈ G and every x ∈ VX.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
subject of group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
that deals with analyzing the algebraic structure of groups acting
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
by automorphisms on simplicial trees
Tree (graph theory)
In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
. The theory relates group actions on trees with decomposing groups as iterated applications of the operations of free product with amalgamation and HNN extension
HNN extension
In mathematics, the HNN extension is a basic construction of combinatorial group theory.Introduced in a 1949 paper Embedding Theorems for Groups by Graham Higman, B. H...
, via the notion of the fundamental group of a graph of groups
Graph of groups
In geometric group theory, a graph of groups is an object consisting of a collection of groups indexed by the vertices and edges of a graph, together with a family of monomorphisms of the edge groups into the vertex groups....
.
Bass–Serre theory can be regarded as one-dimensional version of the orbifold theory
Orbifold
In the mathematical disciplines of topology, geometry, and geometric group theory, an orbifold is a generalization of a manifold...
.
History
Bass–Serre theory was developed by Jean-Pierre SerreJean-Pierre Serre
Jean-Pierre Serre is a French mathematician. He has made contributions in the fields of algebraic geometry, number theory, and topology.-Early years:...
in 1970s and formalized in Trees, Serre's seminal 1977 monograph (developed in collaboration with Hyman Bass
Hyman Bass
Hyman Bass is an American mathematician, known for work in algebra and in mathematics education. From 1959-1998 he was Professor in the Mathematics Department at Columbia University, where he is now professor emeritus...
) on the subject. Serre's original motivation was to understand the structure of certain algebraic group
Algebraic group
In algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
s whose Bruhat–Tits building
Bruhat–Tits building
In mathematics, a building is a combinatorial and geometric structure which simultaneously generalizes certain aspects of flag manifolds, finite projective planes, and Riemannian symmetric spaces...
s are trees. However, the theory quickly became a standard tool of geometric group theory
Geometric group theory
Geometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act .Another important...
and geometric topology
Geometric topology
In mathematics, geometric topology is the study of manifolds and maps between them, particularly embeddings of one manifold into another.- Topics :...
, particularly the study of 3-manifold
3-manifold
In mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
s. Subsequent work of Hyman Bass
Hyman Bass
Hyman Bass is an American mathematician, known for work in algebra and in mathematics education. From 1959-1998 he was Professor in the Mathematics Department at Columbia University, where he is now professor emeritus...
contributed substantially to the formalization and development of basic tools of the theory and currently the term "Bass–Serre theory" is widely used to describe the subject.
Mathematically, Bass–Serre theory builds on exploiting and generalizing the properties of two older group-theoretic constructions: free product with amalgamation and HNN extension
HNN extension
In mathematics, the HNN extension is a basic construction of combinatorial group theory.Introduced in a 1949 paper Embedding Theorems for Groups by Graham Higman, B. H...
. However, unlike the traditional algebraic study of these two constructions, Bass–Serre theory uses the geometric language of covering theory and fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
s. Graphs of groups, which are the basic objects of Bass–Serre theory, can be viewed as one-dimensional versions of orbifold
Orbifold
In the mathematical disciplines of topology, geometry, and geometric group theory, an orbifold is a generalization of a manifold...
s.
Apart from Serre's book, the basic treatment of Bass–Serre theory is available in the article of Bass, the article of Scott and Wall and the books of Hatcher
Allen Hatcher
Allen Edward Hatcher is an American topologist and also a noted author. His book Algebraic Topology, which is the first in a series, is considered by many to be one of the best introductions to the subject....
, Baumslag
Gilbert Baumslag
Gilbert Baumslag is a Distinguished Professor at the City College of New York, with joint appointments in mathematics, computer science, and electrical engineering. He is director of the Center for Algorithms and Interactive Scientific Software, which grew out of the MAGNUS computational group...
, Dicks and Dunwoody
Martin Dunwoody
Martin John Dunwoody is an Emeritus Professor of mathematics at the University of Southampton, England.He earned his Ph.D. in 1964 from the Australian National University. He held positions at the University of Sussex before becoming full Professor at the University of Southampton in 1992...
and Cohen.
Graphs in the sense of Serre
Serre's formalism of graphsGraph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
is slightly different from the standard set-up of graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
. Here a graph A consists of a vertex set V, an edge set E, an edge reversal map
 such that
such that 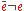 and
and  for every
for every  , and an initial vertex map
, and an initial vertex map  . Thus in A every edge e comes equipped with its formal inverse
. Thus in A every edge e comes equipped with its formal inverse 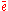 . The vertex o(e) is called the origin or the initial vertex of e and the vertex
. The vertex o(e) is called the origin or the initial vertex of e and the vertex  is called the terminus of e and is denoted t(e). Both loop-edges (that is, edges e such that o(e) = t(e)) and multiple edges are allowed. An orientation on A is a partition of E into the union of two disjoint subsets E+ and E− so that for every edge e exactly one of the edges from the pair
is called the terminus of e and is denoted t(e). Both loop-edges (that is, edges e such that o(e) = t(e)) and multiple edges are allowed. An orientation on A is a partition of E into the union of two disjoint subsets E+ and E− so that for every edge e exactly one of the edges from the pair  belongs to E+ and the other belongs to E−.
belongs to E+ and the other belongs to E−.Graphs of groups
A graph of groupsGraph of groups
In geometric group theory, a graph of groups is an object consisting of a collection of groups indexed by the vertices and edges of a graph, together with a family of monomorphisms of the edge groups into the vertex groups....
A consists of the following data:
- A connected graph A;
- An assignment of a vertex group Av to every vertex v of A.
- An assignment of an edge group Ae to every edge e of A so that we have
 for every e ∈ E.
for every e ∈ E. - Boundary monomorphisms
 for all edges e of A, so that each αe is an injective group homomorphismGroup homomorphismIn mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
for all edges e of A, so that each αe is an injective group homomorphismGroup homomorphismIn mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
.
For every e∈E the map
 is also denoted by ωe.
is also denoted by ωe.Fundamental group of a graph of groups
There are two equivalent definitions of the notion of the fundamental group of a graph of groups: the first is a direct algebraic definition via an explicit group presentation (as a certain iterated application of amalgamated free products and HNN extensionHNN extension
In mathematics, the HNN extension is a basic construction of combinatorial group theory.Introduced in a 1949 paper Embedding Theorems for Groups by Graham Higman, B. H...
s), and the second using the language of groupoid
Groupoid
In mathematics, especially in category theory and homotopy theory, a groupoid generalises the notion of group in several equivalent ways. A groupoid can be seen as a:...
s.
The algebraic definition is easier to state:
First, choose a spanning tree
Spanning tree (mathematics)
In the mathematical field of graph theory, a spanning tree T of a connected, undirected graph G is a tree composed of all the vertices and some of the edges of G. Informally, a spanning tree of G is a selection of edges of G that form a tree spanning every vertex...
T in A. The fundamental group of A with respect to T, denoted
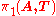 , is defined as the quotient of the free product
, is defined as the quotient of the free productFree product
In mathematics, specifically group theory, the free product is an operation that takes two groups G and H and constructs a new group G ∗ H. The result contains both G and H as subgroups, is generated by the elements of these subgroups, and is the “most general” group having these properties...
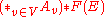
where F(E) is a free group
Free group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
with free basis E, subject to the following relations:
 for every e in E and every
for every e in E and every  . (The so-called Bass–Serre relation.)
. (The so-called Bass–Serre relation.) for every
for every  .
. for every edge e of the spanning tree T.
for every edge e of the spanning tree T.
There is also a notion of the fundamental group of A with respect to a base-vertex
 , denoted
, denoted 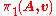 , which is defined using the formalism of groupoid
, which is defined using the formalism of groupoidGroupoid
In mathematics, especially in category theory and homotopy theory, a groupoid generalises the notion of group in several equivalent ways. A groupoid can be seen as a:...
s. It turns out that for every choice of a base-vertex v and every spanning tree T in A the groups
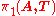 and
and 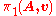 are naturally isomorphic
are naturally isomorphicGroup isomorphism
In abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
.
Fundamental groups of graphs of groups as iterations of amalgamated products and HNN-extensions
The group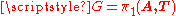 defined above admits an algebraic description in terms of iterated amalgamated free products and HNN extension
defined above admits an algebraic description in terms of iterated amalgamated free products and HNN extensionHNN extension
In mathematics, the HNN extension is a basic construction of combinatorial group theory.Introduced in a 1949 paper Embedding Theorems for Groups by Graham Higman, B. H...
s. First, form a group B as a quotient of the free product

subject to the relations
- e-1αe(g)e=ωe(g) for every e in E+T and every
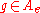 .
. - e=1 for every e in E+T.
This presentation can be rewritten as
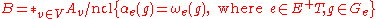
which shows that B is an iterated amalgamated free product of the vertex groups Av.
Then the group
 has the presentation
has the presentation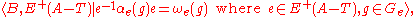
which shows that
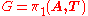 is a multiple HNN extension
is a multiple HNN extensionHNN extension
In mathematics, the HNN extension is a basic construction of combinatorial group theory.Introduced in a 1949 paper Embedding Theorems for Groups by Graham Higman, B. H...
of B with stable letters
 .
.Splittings
An isomorphism between a group G and the fundamental group of a graph of groups is called a splitting of G. If the edge groups in the splitting come from a particular class of groups (e.g. finite, cyclic, abelian, etc.), the splitting is said to be a splitting over that class.Thus a splitting where all edge groups are finite is called a splitting over finite groups.
Algebraically, a splitting of G with trivial edge groups corresponds to a free product decomposition

where F(X) is a free group
Free group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
with free basis X=E+(A-T) consisting of all positively oriented edges (with respect to some orientation on A) in the complement of some spanning tree T of A.
The normal forms theorem
Let g be an element of represented as a product of the form
represented as a product of the form
where e1,..., en is a closed edge-path in A with the vertex sequence v0, v1,...,vn=v0 (that is v0=o(e1), vn=t(en) and vi=t(ei)=o(ei+1) for 0 < i < n) and where
 for i = 0, ..., n.
for i = 0, ..., n.Suppose that g = 1 in G. Then
- either n=0 and a0=1 in
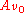 ,
, - or n > 0 and there is some 0 < i < n such that
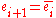 and
and 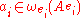 .
.
The normal forms theorem immediately implies that the canonical homomorphisms
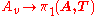 are injective, so that we can think of the vertex groups Av as subgroups of G.
are injective, so that we can think of the vertex groups Av as subgroups of G.Higgins has given a nice version of the normal form using the fundamental groupoid
Groupoid
In mathematics, especially in category theory and homotopy theory, a groupoid generalises the notion of group in several equivalent ways. A groupoid can be seen as a:...
of a graph of groups. This avoids choosing a base point or tree, and has been exploited in.
Bass–Serre covering trees
To every graph of groups A, with a specified choice of a base-vertex, one can associate a Bass–Serre covering tree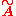 , which is a tree that comes equipped with a natural group action
, which is a tree that comes equipped with a natural group actionGroup action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
of the fundamental group
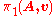 without edge-inversions.
without edge-inversions.Moreover, the quotient graph
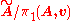 is isomorphic to A.
is isomorphic to A.Similarly, if G is a group acting on a tree X without edge-inversions (that is, so that for every edge e of X and every g in G we have
 ), one can define the natural notion of a quotient graph of groups A. The underlying graph A of A is the quotient graph X/G. The vertex groups of A are isomorphic to vertex stabilizers in G of vertices of X and the edge groups of A are isomorphic to edge stabilizers in G of edges of X.
), one can define the natural notion of a quotient graph of groups A. The underlying graph A of A is the quotient graph X/G. The vertex groups of A are isomorphic to vertex stabilizers in G of vertices of X and the edge groups of A are isomorphic to edge stabilizers in G of edges of X.Moreover, if X was the Bass–Serre covering tree of a graph of groups A and if
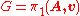 then the quotient graph of groups for the action of G on X can be chosen to be naturally isomorphic to A.
then the quotient graph of groups for the action of G on X can be chosen to be naturally isomorphic to A.Fundamental theorem of Bass–Serre theory
Let G be a group acting on a tree X without inversions. Let A be the quotient graph of groups and let v be a base-vertex in A. Then G is isomorphic to the group and there is an equivariant isomorphism between the tree X and the Bass–Serre covering tree
and there is an equivariant isomorphism between the tree X and the Bass–Serre covering tree 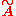 . More precisely, there is a group isomorphism
. More precisely, there is a group isomorphismGroup isomorphism
In abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
 and a graph isomorphism
and a graph isomorphism 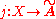 such that for every g in G, for every vertex x of X and for every edge e of X we have j(gx) = g j(x) and j(ge) = g j(e).
such that for every g in G, for every vertex x of X and for every edge e of X we have j(gx) = g j(x) and j(ge) = g j(e).One of the immediate consequences of the above result is the classic Kurosh subgroup theorem
Kurosh subgroup theorem
In the mathematical field of group theory, the Kurosh subgroup theorem describes the algebraic structure of subgroups of free products of groups. The theorem was obtained by Alexander Kurosh, a Russian mathematician, in 1934...
describing the algebraic structure of subgroups of free product
Free product
In mathematics, specifically group theory, the free product is an operation that takes two groups G and H and constructs a new group G ∗ H. The result contains both G and H as subgroups, is generated by the elements of these subgroups, and is the “most general” group having these properties...
s.
Amalgamated free product
Consider a graph of groups A consisting of a single non-loop edge e (together with its formal inverse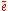 ) with two distinct end-vertices u = o(e) and v = t(e), vertex groups H=Au, K=Av, an edge group C=Ae and the boundary monomorphisms
) with two distinct end-vertices u = o(e) and v = t(e), vertex groups H=Au, K=Av, an edge group C=Ae and the boundary monomorphisms 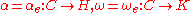 .
.Then T = A is a spanning tree in A and the fundamental group
 is isomorphic to the amalgamated free product
is isomorphic to the amalgamated free product
In this case the Bass–Serre tree
 can be described as follows. The vertex set of X is the set of coset
can be described as follows. The vertex set of X is the set of cosetCoset
In mathematics, if G is a group, and H is a subgroup of G, and g is an element of G, thenA coset is a left or right coset of some subgroup in G...
s

Two vertices gK and fH are adjacent in X whenever there exists k ∈ K such that fH = gkH (or, equivalently, whenever there is h ∈ H such that gK = fhK).
The G-stabilizer of every vertex of X of type gK is equal to gKg−1 and the G-stabilizer of every vertex of X of type gH is equal to gHg−1. For an edge [gH, ghK] of X its G-stabilizer is equal to ghα(C)h−1g−1.
For every c ∈ C and h ∈ 'k ∈ K' the edges [gH, ghK] and [gH, ghα(c)K] are equal and the degree of the vertex gH in X is equal to the index
Index of a subgroup
In mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
[H:α(C)].
Similarly, every vertex of type gK has degree [K:ω(C)] in X.
HNN extension
Let A be a graph of groups consisting of a single loop-edge e (together with its formal inverse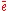 ), a single vertex v = o(e) = t(e), a vertex group B = Av, an edge group C = Ae and the boundary monomorphisms
), a single vertex v = o(e) = t(e), a vertex group B = Av, an edge group C = Ae and the boundary monomorphisms 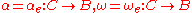 .
.Then T = v is a spanning tree in A and the fundamental group
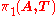 is isomorphic to the HNN extension
is isomorphic to the HNN extensionHNN extension
In mathematics, the HNN extension is a basic construction of combinatorial group theory.Introduced in a 1949 paper Embedding Theorems for Groups by Graham Higman, B. H...
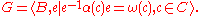
with the base group B, stable letter e and the associated subgroups H = α(C), K = ω(C) in B.
The composition
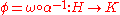 is an isomorphism and the above HNN-extension presentation of G can be rewritten as
is an isomorphism and the above HNN-extension presentation of G can be rewritten as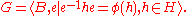
In this case the Bass–Serre tree
 can be described as follows. The vertex set of X is the set of coset
can be described as follows. The vertex set of X is the set of cosetCoset
In mathematics, if G is a group, and H is a subgroup of G, and g is an element of G, thenA coset is a left or right coset of some subgroup in G...
s
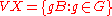 .
.Two vertices gB and fB are adjacent in X whenever there exists
 such that either fB = gbeB or fB = gbe−1B. The G-stabilizer of every vertex of X is conjugate to B in G and the stabilizer of every edge of X is conjugate to H in G. Every vertex of X has degree equal to [B : H] + [B : K].
such that either fB = gbeB or fB = gbe−1B. The G-stabilizer of every vertex of X is conjugate to B in G and the stabilizer of every edge of X is conjugate to H in G. Every vertex of X has degree equal to [B : H] + [B : K].A graph with the trivial graph of groups structure
Let A be a graph of groups with underlying graph A such that all the vertex and edge groups in A are trivial. Let v be a base-vertex in A. Then π1(A,v) is equal to the fundamental groupFundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
π1(A,v) of the underlying graph A in the standard sense of algebraic topology and the Bass–Serre covering tree
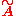 is equal to the standard universal covering space
is equal to the standard universal covering space 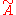 of A. Moreover, the action of π1(A,v) on
of A. Moreover, the action of π1(A,v) on 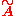 is exactly the standard action of π1(A,v) on
is exactly the standard action of π1(A,v) on 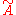 by deck transformations.
by deck transformations.Basic facts and properties
- If A is a graph of groups with a spanning tree T and if
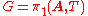 , then for every vertex v of A the canonical homomorphism from Av to G is injective.
, then for every vertex v of A the canonical homomorphism from Av to G is injective. - If
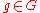 is an element of finite order then g is conjugate in G to an element of finite order in some vertex group Av.
is an element of finite order then g is conjugate in G to an element of finite order in some vertex group Av. - If
 is a finite subgroup then F is conjugate in G to a subgroup of some vertex group Av.
is a finite subgroup then F is conjugate in G to a subgroup of some vertex group Av. - If the graph A is finite and all vertex groups Av are finite then the group G is virtually free, that is, G contains a free subgroup of finite index.
- If A is finite and all the vertex groups Av are finitely generated then G is finitely generated.
- If A is finite and all the vertex groups Av are finitely presented and all the edge groups Ae are finitely generated then G is finitely presented.
Trivial and nontrivial actions
A graph of groups A is called trivial if A = T is already a tree and there is some vertex v of A such that . This is equivalent to the condition that A is a tree and that for every edge e = [u, z] of A (with o(e) = u, t(e) = z) such that u is closer to v than z we have [Az : ωe(Ae)] = 1, that is Az = ωe(Ae).
. This is equivalent to the condition that A is a tree and that for every edge e = [u, z] of A (with o(e) = u, t(e) = z) such that u is closer to v than z we have [Az : ωe(Ae)] = 1, that is Az = ωe(Ae).An action of a group G on a tree X without edge-inversions is called trivial if there exists a vertex x of X that is fixed by G, that is such that Gx = x. It is known that an action of G on X is trivial if and only if the quotient graph of groups for that action is trivial.
Typically, only nontrivial actions on trees are studied in Bass–Serre theory since trivial graphs of groups do not carry any interesting algebraic information, although trivial actions in the above sense (e. g. actions of groups by automorphisms on rooted trees) may also be interesting for other mathematical reasons.
One of the classic and still important results of the theory is a theorem of Stallings about ends of groups. The theorem states that a finitely generated group has more than one end if and only if this group admits a nontrivial splitting over finite subroups that is, if and only if the group admits a nontrivial action without inversions on a tree with finite edge stabilizers.
An important general result of the theory states that if G is a group with Kazhdan's property (T)
Kazhdan's property (T)
In mathematics, a locally compact topological group G has property if the trivial representation is an isolated point in its unitary dual equipped with the Fell topology. Informally, this means that if G acts unitarily on a Hilbert space and has "almost invariant vectors", then it has a nonzero...
then G does not admit any nontrivial splitting, that is, that any action of G on a tree X without edge-inversions has a global fixed vertex.
Hyperbolic length functions
Let G be a group acting on a tree X without edge-inversions.For every g∈G put
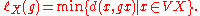
Then
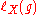 is called the translation length of g on X.
is called the translation length of g on X.The function

is called the hyperbolic length function or the translation length function for the action of G on X.
Basic facts regarding hyperbolic length functions
- For g ∈ G exactly one of the following holds:
 and g fixes a vertex of G. In this case g is called an elliptic element of G.
and g fixes a vertex of G. In this case g is called an elliptic element of G.  and there is a unique bi-infinite embedded line in X, called the axis of g and denoted Lg which is g-invariant. In this case g acts on Lg by translation of magnitude
and there is a unique bi-infinite embedded line in X, called the axis of g and denoted Lg which is g-invariant. In this case g acts on Lg by translation of magnitude 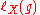 and the element g ∈ G is called hyperbolic.
and the element g ∈ G is called hyperbolic. - If
 then there exists a unique minimal G-invariant subtree XG of X. Moreover XG is equal to the union of axes of hyperbolic elements of G.
then there exists a unique minimal G-invariant subtree XG of X. Moreover XG is equal to the union of axes of hyperbolic elements of G.
The length-function
 is said to be abelian if it is a group homomorphism
is said to be abelian if it is a group homomorphismGroup homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
from G to
 and non-abelian otherwise. Similarly, the action of G on X is said to be abelian if the associated hyperbolic length function is abelian and is said to be non-abelian otherwise.
and non-abelian otherwise. Similarly, the action of G on X is said to be abelian if the associated hyperbolic length function is abelian and is said to be non-abelian otherwise.In general, an action of G on a tree X without edge-inversions is said to be minimal if there are no proper G-invariant subtrees in X.
An important fact in the theory says that minimal non-abelian tree actions are uniquely determined by their hyperbolic length functions:
Uniqueness theorem
Let G be a group with two nonabelian minimal actions without edge-inversions on trees X and Y. Suppose that the hyperbolic length functions ℓX and ℓY on G are equal, that is ℓX(g) = ℓY(g) for every g ∈ G. Then the actions of G on X and Y are equal in the sense that there exists a graph isomorphismGraph isomorphism
In graph theory, an isomorphism of graphs G and H is a bijection between the vertex sets of G and H f \colon V \to V \,\!such that any two vertices u and v of G are adjacent in G if and only if ƒ and ƒ are adjacent in H...
f : X → Y which is G-equivariant, that is f(gx) = g f(x) for every g ∈ G and every x ∈ VX.
Important developments in Bass–Serre theory
Important developments in Bass–Serre theory in the last 30 years include:- Various accessibility results for finitely presented groups that bound the complexity (that is, the number of edges) in a graph of groups decomposition of a finitely presented group, where some algebraic or geometric restrictions on the types of groups considered are imposed. These results include:
- Dunwoody'sMartin DunwoodyMartin John Dunwoody is an Emeritus Professor of mathematics at the University of Southampton, England.He earned his Ph.D. in 1964 from the Australian National University. He held positions at the University of Sussex before becoming full Professor at the University of Southampton in 1992...
theorem about accessibility of finitely presented groups stating that for any finitely presented group G there exists a bound on the complexity of splittings of G over finite subgroups (the splittings are required to satisfy a technical assumption of being "reduced"); - Bestvina–Feighn generalized accessibility theorem stating that for any finitely presented group G there is a bound on the complexity of reduced splittings of G over small subgroups (the class of small groups includes, in particular, all groups that do not contain non-abelian free subgroups);
- Acylindrical accessibility results for finitely presented (Sela, Delzant) and finitely generated (Weidmann) groups which bound the complexity of the so-called acylindrical splittings, that is splittings where for their Bass–Serre covering trees the diameters of fixed subsets of nontrivial elements of G are uniformly bounded.
- Dunwoody's
- The theory of JSJ-decompositions for finitely presented groups. This theory was motivated by the classic notion of JSJ decompositionJSJ decompositionIn mathematics, the JSJ decomposition, also known as the toral decomposition, is a topological construct given by the following theorem:The acronym JSJ is for William Jaco, Peter Shalen, and Klaus Johannson...
in 3-manifold topology3-manifoldIn mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
and was initiated, in the context of word-hyperbolic groups, by the work of Sela. JSJ decompositions are splittings of finitely presented groups over some classes of small subgroups (cyclic, abelian, noetherian, etc., depending on the version of the theory) that provide a canonical descriptions, in terms of some standard moves, of all splittings of the group over subgroups of the class. There are a number of versions of JSJ-decomposition theories:- The initial version of Sela for cyclic splittings of torsion-free word-hyperbolic groups.
- Bowditch'sBrian BowditchBrian Hayward Bowditch is a British mathematician known for his contributions to geometry and topology, particularly in the areas of geometric group theory and low-dimensional topology. He is also known for solving the angel problem...
version of JSJ theory for word-hyperbolic groups (with possible torsion) encoding their splittings over virtually cyclic subgroups. - The version of Rips and Sela of JSJ decompositions of torsion-free finitely presented groups encoding their splittings over free abelian subgroupsFree abelian groupIn abstract algebra, a free abelian group is an abelian group that has a "basis" in the sense that every element of the group can be written in one and only one way as a finite linear combination of elements of the basis, with integer coefficients. Hence, free abelian groups over a basis B are...
. - The version of Dunwoody and Sageev of JSJ decompositions of finitely presented groups over noetherian subgroups.
- The version of Fujiwara and Papasoglu, also of JSJ decompositions of finitely presented groups over noetherian subgroups.
- A version of JSJ decomposition theory for finitely presented groups developed by Scott and Swarup.
- The theory of lattices in automorphism groups of trees. The theory of tree lattices was developed by Bass, Kulkarni and LubotzkyAlexander LubotzkyProfessor Alexander Lubotzky is an Israeli academic and former politician. A former head of the Mathematics Institute at the Hebrew University of Jerusalem, he served as a member of the Knesset for The Third Way party between 1996 and 1999.-Education:...
by analogy with the theory of latticesLattice (discrete subgroup)In Lie theory and related areas of mathematics, a lattice in a locally compact topological group is a discrete subgroup with the property that the quotient space has finite invariant measure...
in Lie groupLie groupIn mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s (that is discrete subgroups of Lie groupLie groupIn mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s of finite co-volume). For a discrete subgroup G of the automorphism group of a locally finite tree X one can define a natural notion of volume for the quotient graph of groups A as
-
- The group G is called an X-lattice if
 . The theory of tree lattices turns out to be useful in the study of discrete subgroups of algebraic groupAlgebraic groupIn algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
. The theory of tree lattices turns out to be useful in the study of discrete subgroups of algebraic groupAlgebraic groupIn algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
s over non-archimedean local fieldsLocal fieldIn mathematics, a local field is a special type of field that is a locally compact topological field with respect to a non-discrete topology.Given such a field, an absolute value can be defined on it. There are two basic types of local field: those in which the absolute value is archimedean and...
and in the study of Kac–Moody groups.- Development of foldinds and Nielsen methods for approximating group actions on trees and analyzing their subgroup structure.
- The theory of ends and relative ends of groups, particularly various generalizations of Stallings theorem about groups with more than one end.
- Quasi-isometric rigidity results for groups acting on trees.
Generalizations
There have been several generalizations of Bass–Serre theory:- The theory of complexes of groups (see Haefliger, Corson Bridson-Haefliger) provides a higher-dimensional generalization of Bass–Serre theory. The notion of a graph of groupsGraph of groupsIn geometric group theory, a graph of groups is an object consisting of a collection of groups indexed by the vertices and edges of a graph, together with a family of monomorphisms of the edge groups into the vertex groups....
is replaced by that of a complex of groups, where groups are assigned to each cell in a simplicial complex, together with monomorphisms between these groups corresponding to face inclusions (these monomorphisms are required to satisfy certain compatibility conditions). One can then define an analog of the fundamental group of a graph of groups for a complex of groups. However, in order for this notion to have good algebraic properties (such as embeddability of the vertex groups in it) and in order for a good analog for the notion of the Bass–Serre covering tree to exist in this context, one needs to require some sort of "non-positive curvature" condition for the complex of groups in question (see, for example ). - The theory of isometric group actions on real treeReal treeA real tree, or an \mathbb R-tree, is a metric space such thatfor any x, y in M there is a unique arc from x to y and this arc is a geodesic segment. Here by an arc from x to y we mean the image in M of a topological embedding f from an interval [a,b] to M such that f=x and f=y...
s (or -trees) which are metric spaceMetric spaceIn mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
-trees) which are metric spaceMetric spaceIn mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
s generalizing the graph-theoretic notion of a tree (graph theory)Tree (graph theory)In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
. The theory was developed largely in the 1990s, where the Rips machineRips machineIn geometric group theory, the Rips machine is a method of studying the action of groups on R-trees. It was introduced in unpublished work of Eliyahu Rips in about 1991....
of Eliyahu RipsEliyahu RipsEliyahu Rips, also Ilya Rips is a Latvian-born Israeli mathematician known for his research in geometric group theory. He became known to the general public following his coauthoring a paper on the Torah Code....
on the structure theory of stable group actions on -trees played a key role (see Bestvina-Feighn). This structure theory assigns to a stable isometric action of a finitely generated group G a certain "normal form" approximation of that action by a stable action of G on a simplicial tree and hence a splitting of G in the sense of Bass–Serre theory. Group actions on real treeReal treeA real tree, or an \mathbb R-tree, is a metric space such thatfor any x, y in M there is a unique arc from x to y and this arc is a geodesic segment. Here by an arc from x to y we mean the image in M of a topological embedding f from an interval [a,b] to M such that f=x and f=y...
-trees played a key role (see Bestvina-Feighn). This structure theory assigns to a stable isometric action of a finitely generated group G a certain "normal form" approximation of that action by a stable action of G on a simplicial tree and hence a splitting of G in the sense of Bass–Serre theory. Group actions on real treeReal treeA real tree, or an \mathbb R-tree, is a metric space such thatfor any x, y in M there is a unique arc from x to y and this arc is a geodesic segment. Here by an arc from x to y we mean the image in M of a topological embedding f from an interval [a,b] to M such that f=x and f=y...
s arise naturally in several contexts in geometric topologyGeometric topologyIn mathematics, geometric topology is the study of manifolds and maps between them, particularly embeddings of one manifold into another.- Topics :...
: for example as boundary points of the Teichmüller spaceTeichmüller spaceIn mathematics, the Teichmüller space TX of a topological surface X, is a space that parameterizes complex structures on X up to the action of homeomorphisms that are isotopic to the identity homeomorphism...
(every point in the Thurston boundary of the Teichmüller space is represented by a measured geodesic lamination on the surface; this lamination lifts to the universal cover of the surface and a naturally dual object to that lift is an -tree endowed with an isometric action of the fundamental group of the surface), as Gromov-Hausdorff limitsGromov-Hausdorff convergenceIn mathematics, Gromov–Hausdorff convergence, named after Mikhail Gromov and Felix Hausdorff, is a notion for convergence of metric spaces which is a generalization of Hausdorff convergence.-Gromov–Hausdorff distance:...
-tree endowed with an isometric action of the fundamental group of the surface), as Gromov-Hausdorff limitsGromov-Hausdorff convergenceIn mathematics, Gromov–Hausdorff convergence, named after Mikhail Gromov and Felix Hausdorff, is a notion for convergence of metric spaces which is a generalization of Hausdorff convergence.-Gromov–Hausdorff distance:...
of, appropriately rescaled, Kleinian groupKleinian groupIn mathematics, a Kleinian group is a discrete subgroup of PSL. The group PSL of 2 by 2 complex matrices of determinant 1 modulo its center has several natural representations: as conformal transformations of the Riemann sphere, and as orientation-preserving isometries of 3-dimensional hyperbolic...
actions, and so on. The use of -trees machinery provides substantial shortcuts in modern proofs of Thurston's Hyperbolization TheoremGeometrization conjectureThurston's geometrization conjecture states that compact 3-manifolds can be decomposed canonically into submanifolds that have geometric structures. The geometrization conjecture is an analogue for 3-manifolds of the uniformization theorem for surfaces...
-trees machinery provides substantial shortcuts in modern proofs of Thurston's Hyperbolization TheoremGeometrization conjectureThurston's geometrization conjecture states that compact 3-manifolds can be decomposed canonically into submanifolds that have geometric structures. The geometrization conjecture is an analogue for 3-manifolds of the uniformization theorem for surfaces...
for Haken 3-manifoldsHaken manifoldIn mathematics, a Haken manifold is a compact, P²-irreducible 3-manifold that is sufficiently large, meaning that it contains a properly embedded two-sided incompressible surface...
. Similarly, -trees play a key role in the study of CullerMarc CullerMarc Edward Culler is an American mathematician who works in geometric group theory and low-dimensional topology. A native Californian, Culler did his undergraduate work at the University of California at Santa Barbara and his graduate work at Berkeley where he graduated in 1978. He is now at the...
-trees play a key role in the study of CullerMarc CullerMarc Edward Culler is an American mathematician who works in geometric group theory and low-dimensional topology. A native Californian, Culler did his undergraduate work at the University of California at Santa Barbara and his graduate work at Berkeley where he graduated in 1978. He is now at the...
-VogtmannKaren VogtmannKaren Vogtmann is a U.S. mathematician working primarily in the area of geometric group theory. She is known for having introduced, in a 1986 paper with Marc Culler, an object now known as the Culler–Vogtmann Outer space...
's Outer space as well as in other areas of geometric group theoryGeometric group theoryGeometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act .Another important...
; for example, asymptotic cones of groups often have a tree-like structure and give rise to group actions on real treeReal treeA real tree, or an \mathbb R-tree, is a metric space such thatfor any x, y in M there is a unique arc from x to y and this arc is a geodesic segment. Here by an arc from x to y we mean the image in M of a topological embedding f from an interval [a,b] to M such that f=x and f=y...
s. The use of -trees, together with Bass–Serre theory, is a key tool in the work of Sela on solving the isomorphism problem for (torsion-free) word-hyperbolic groups, Sela's version of the JSJ-decomposition theory and the work of Sela on the Tarski Conjecture for free groups and the theory of limit groups.
-trees, together with Bass–Serre theory, is a key tool in the work of Sela on solving the isomorphism problem for (torsion-free) word-hyperbolic groups, Sela's version of the JSJ-decomposition theory and the work of Sela on the Tarski Conjecture for free groups and the theory of limit groups. - The theory of group actions on Λ-trees, where Λ is an ordered abelian groupAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
(such as or
or  ) provides a further generalization of both the Bass–Serre theory and the theory of group actions on
) provides a further generalization of both the Bass–Serre theory and the theory of group actions on  -trees (see Morgan, Alperin-Bass, Chiswell).
-trees (see Morgan, Alperin-Bass, Chiswell).