
Where Mathematics Comes From
Encyclopedia
Where Mathematics Comes From: How the Embodied Mind Brings Mathematics into Being (hereinafter WMCF) is a book by George Lakoff
, a cognitive linguist
, and Rafael E. Núñez
, a psychologist
. Published in 2000, WMCF seeks to found a cognitive science of mathematics, a theory of embodied mathematics based on conceptual metaphor
.
Nikolay Lobachevsky said "There is no branch of mathematics, however abstract, which may not some day be applied to phenomena of the real world." A common type of conceptual blending
process would seem apply to the entire mathematical procession. Pythagoras said "All is number."
ically structure basic arithmetic: object collection, object construction, using a measuring stick, and moving along a path.
WMCF builds on earlier books by Lakoff (1987) and Lakoff and Johnson (1980, 1999), which analyze such concepts of metaphor
and image schemata from second-generation cognitive science
. Some of the riches of these earlier books, such as the interesting technical ideas in Lakoff (1987), are absent from WMCF.
Lakoff and Núñez hold that mathematics results from the human cognitive apparatus and must therefore be understood in cognitive terms. WMCF advocates (and includes some examples of) a cognitive idea analysis of mathematics
which analyzes mathematical ideas in terms of the human experiences, metaphors, generalizations, and other cognitive mechanisms giving rise to them. A standard mathematical education does not develop such idea analysis techniques because it does not pursue considerations of A) what structures of the mind allow it to do mathematics or B) the philosophy of mathematics
.
Lakoff and Núñez start by reviewing the psychological literature, concluding that human beings appear to have an innate ability, called subitizing, to count, add, and subtract up to about 4 or 5. They document this conclusion by reviewing the literature, published in recent decades, describing experiments with infant subjects. For example, infants quickly become excited or curious when presented with "impossible" situations, such as having three toys appear when only two were initially present.
The authors argue that mathematics goes far beyond this very elementary level due to a large number of metaphor
ical constructions. For example, they argue that the Pythagorean
position that all is number, and the associated crisis of confidence that came about with the discovery of the irrationality of the square root of two, arises solely from a metaphorical relation between the length of the diagonal of a square, and the possible numbers of objects.
Much of WMCF deals with the important concepts of infinity
and of limit processes, seeking to explain how finite humans living in a finite world could ultimately conceive of the actual infinite. Thus much of WMCF is, in effect, a study of the epistemological foundations of the calculus
. Lakoff and Núñez conclude that while the potential infinite is not metaphorical, the actual infinite is. Moreover, they deem all manifestations of actual infinity to be instances of what they call the "Basic Metaphor of Infinity", as represented by the ever-increasing sequence 1, 2, 3, ...
WMCF emphatically rejects the Platonistic
philosophy of mathematics
. They emphasize that all we know and can ever know is human mathematics, the mathematics arising from the human intellect. The question of whether there is a "transcendent" mathematics independent of human thought is a meaningless question. That is like asking if colors are transcendent of human thought- colors are only varying wavelengths of light, it is our interpretation of physical stimuli that make them colors.
WMCF (p. 81) likewise criticizes the emphasis mathematicians place on the concept of closure
. Lakoff and Núñez argue that the expectation of closure is an artifact of the human mind's ability to relate fundamentally different concepts via metaphor
.
WMCF concerns itself mainly with proposing and establishing an alternative view of mathematics, one grounding the field in the realities of human biology and experience. It is not a work of technical mathematics or philosophy. Lakoff and Núñez are not the first to argue that conventional approaches to the philosophy of mathematics are flawed. For example, they do not seem all that familiar with the content of Davis and Hersh (1981), even though WMCF warmly acknowledges Reuben Hersh
's support.
Lakoff and Núñez cite Saunders MacLane (the inventor, with Samuel Eilenberg
, of category theory
) in support of their position. MacLane (1986), an overview of mathematics intended for philosophers, proposes that mathematical concepts are ultimately grounded in ordinary human activities, mostly interactions with the physical world. See From Action to Mathematics per Mac Lane.
Educators have taken some interest in what WMCF suggests about how mathematics is learned, and why students find some elementary concepts more difficult than others.
s described in WMCF, in addition to the Basic Metaphor of Infinity, include:
Mathematical reasoning requires variables
ranging over some universe of discourse, so that we can reason about generalities rather than merely about particulars. WMCF argues that reasoning with such variables implicitly relies on what it terms the Fundamental Metonymy
of Algebra.
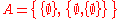 . Then recall two bits of standard terminology from elementary set theory
. Then recall two bits of standard terminology from elementary set theory
:
By (1), A is the set {1,2}. But (1) and (2) together say that A is also the ordered pair (0,1). Both statements cannot be correct; the ordered pair
(0,1) and the unordered pair {1,2} are fully distinct concepts. Lakoff and Johnson (1999) term this situation "metaphorically ambiguous." This simple example calls into question any Platonistic
foundations for mathematics.
While (1) and (2) above are admittedly canonical, especially within the consensus set theory
known as the Zermelo–Fraenkel axiomatization, WMCF does not let on that they are but one of several definitions that have been proposed since the dawning of set theory. For example, Frege, Principia Mathematica
, and New Foundations
(a body of axiomatic set theory begun by Quine
in 1937) define cardinals
and ordinals
as equivalence classes under the relations
of equinumerosity
and similarity
, so that this conundrum does not arise. In Quinian set theory, A is simply an instance of the number 2. For technical reasons, defining the ordered pair as in (2) above is awkward in Quinian set theory. Two solutions have been proposed:
one can indeed have {1,2} = (0,1), as these are two different symbols denoting the same object. The claim that there is an anomaly because these are "fully distinct concepts" is on the one hand not a clear scientific statement, and on the other hand, is on par with such statements as: ""The positive real solution of " and "
" and " " cannot be equal because they are fully distinct concepts.".
" cannot be equal because they are fully distinct concepts.".
The apparent anomaly stems from the fact that Lakoff and Núñez identify mathematical objects with their various particular realizations. There are several equivalent definitions of ordered pair, and most mathematicians do not identify the ordered pair with just one of these definitions (since this would be an arbitrary and artificial choice), but view the definitions as equivalent models or realizations of the same underlying object. The existence of several different but equivalent constructions of certain mathematical objects supports the platonistic view that the mathematical objects exist beyond their various linguistical, symbolical, or conceptual representations.
As an example, many mathematicians would favour a definition of ordered pair in terms of category theory where the object in question is defined in terms of a characteristic universal property and then shown to be unique up to unique isomorphism (this was recently mentioned in an article on mathematical platonism by David Mumford).
The above discussion is meant to explain that the most natural and fruitful approach in mathematics is to view a mathematical object as having potentially several different but equivalent realizations. On the other hand, the object is not identified with just one of these realizations. This suggests that the intuitionistic idea that mathematical objects exist only as specific mental constructions, or the idea of Lakoff and Núñez that mathematical objects exist only as particular instances of concepts/metaphors in our embodied brains, is an inadequate philosophical basis to account for the experience and de facto research methods of working mathematicians. Perhaps this is a reason why these ideas have been met with comparatively little interest by the mathematical community.
It is very much an open question whether WMCF will eventually prove to be the start of a new school in the philosophy of mathematics
. Hence the main value of WMCF so far may be a critical one: its critique of Platonism
in mathematics, and the Romance of Mathematics.
means exactly what it meant when Fermat initially proposed it 1664. Other reviewers have pointed out that multiple conceptual strategies can be employed in connection with the same mathematically defined term, often by the same person (a point that is compatible with the view that we routinely understand the 'same' concept with different metaphors). The metaphor
and the conceptual strategy are not the same as the formal definition
which mathematicians employ. However, WMCF points out that formal definitions are built using words and symbols that have meaning only in terms of human experience.
Critiques of WMCF include the humorous:
and the physically informed:
Mathematicians have also complained that Lakoff and Núñez have misunderstood some basic mathematical notions. The authors reply that the errors found in earlier printings of WMCF are now corrected.
Lakoff made his reputation by linking linguistics
to cognitive science
and the analysis of metaphor
. Núñez, educated in Switzerland
, is a product of Jean Piaget
's school of cognitive psychology
as a basis for logic and mathematics. Núñez has thought much about the foundations of real analysis
, the real
and complex number
s, and the Basic Metaphor of Infinity. These topics, however, worthy though they be, form part of the superstructure of mathematics. Cognitive science should take more interest in the foundations of mathematics
. And indeed, the authors do pay a fair bit of attention early on to logic
, Boolean algebra and the Zermelo–Fraenkel axioms, even lingering a bit over group theory
. But neither author is well-trained in logic
(there is no index entry for "quantifier" or "quantification"), the philosophy of set theory, the axiomatic method, metamathematics, and model theory
. Nor does WMCF say enough about the derivation of number system
s (the Peano axioms
go unmentioned), abstract algebra
, equivalence
and order relations, mereology
, topology
, and geometry
.
Lakoff and Núñez tend to dismiss the negative opinions mathematicians have expressed about WMCF, because their critics do not appreciate the insights of cognitive science. Lakoff and Núñez maintain that their argument can only be understood using the discoveries of recent decades about the way human brains process language and meaning. They argue that any arguments or criticisms that are not grounded in this understanding cannot address the content of the book.
It has been pointed out that it is not at all clear that WMCF establishes that the claim "intelligent alien life would have mathematical ability" is a myth. To do this, it would be required to show that intelligence and mathematical ability are separable, and this has not been done. On Earth, intelligence and mathematical ability seem to go hand in hand in all life-forms, as pointed out by Keith Devlin
among others. The authors of WMCF have not explained how this situation would (or even could) be different anywhere else.
Lakoff and Núñez also appear not to appreciate the extent to which intuitionists and constructivist
s have anticipated their attack on the Romance of (Platonic) Mathematics. Brouwer
, the founder of the intuitionist/constructivist
point of view, wrote "Mathematics is a free construction of the human mind." Hence at least one person writing before Lakoff and Núñez were born concluded that mathematics emerged to serve human purposes and has no existence apart from this fact.
The cognitive approach to formal system
s, as described and implemented in WMCF, need not be confined to mathematics, but should also prove fruitful when applied to formal logic, and to formal philosophy such as Edward Zalta's theory of abstract objects. Lakoff and Johnson (1999) fruitfully employ the cognitive approach to rethink a good deal of the philosophy of mind
, epistemology, metaphysics
, and the history of ideas
.
George Lakoff
George P. Lakoff is an American cognitive linguist and professor of linguistics at the University of California, Berkeley, where he has taught since 1972...
, a cognitive linguist
Cognitive linguistics
In linguistics, cognitive linguistics refers to the branch of linguistics that interprets language in terms of the concepts, sometimes universal, sometimes specific to a particular tongue, which underlie its forms...
, and Rafael E. Núñez
Rafael E. Núñez
Rafael E. Núñez is a professor of cognitive science at the University of California, San Diego and a proponent of embodied cognition. He co-authored Where Mathematics Comes From with George Lakoff.-External links:*...
, a psychologist
Psychologist
Psychologist is a professional or academic title used by individuals who are either:* Clinical professionals who work with patients in a variety of therapeutic contexts .* Scientists conducting psychological research or teaching psychology in a college...
. Published in 2000, WMCF seeks to found a cognitive science of mathematics, a theory of embodied mathematics based on conceptual metaphor
Conceptual metaphor
In cognitive linguistics, conceptual metaphor, or cognitive metaphor, refers to the understanding of one idea, or conceptual domain, in terms of another, for example, understanding quantity in terms of directionality . A conceptual domain can be any coherent organization of human experience...
.
WMCF definition of mathematics
Mathematics makes up that part of the human conceptual system that is special in the following way:- "It is precise, consistent, stable across time and human communities, symbolizable, calculable, generalizable, universally available, consistent within each of its subject matters, and effective as a general tool for description, explanation, and prediction in a vast number of everyday activities, [ranging from] sports, to building, business, technology, and science." (WMCF, pp. 50, 377)
Nikolay Lobachevsky said "There is no branch of mathematics, however abstract, which may not some day be applied to phenomena of the real world." A common type of conceptual blending
Conceptual blending
Conceptual Blending is a general theory of cognition. According to this theory, elements and vital relations from diverse scenarios are "blended" in a subconscious process known as Conceptual Blending, which is assumed to be ubiquitous to everyday thought and language...
process would seem apply to the entire mathematical procession. Pythagoras said "All is number."
Human cognition and mathematics
Lakoff and Núñez's avowed purpose is to begin laying the foundations for a truly scientific understanding of mathematics, one grounded in processes common to all human cognition. They find that four distinct but related processes metaphorMetaphor
A metaphor is a literary figure of speech that uses an image, story or tangible thing to represent a less tangible thing or some intangible quality or idea; e.g., "Her eyes were glistening jewels." Metaphor may also be used for any rhetorical figures of speech that achieve their effects via...
ically structure basic arithmetic: object collection, object construction, using a measuring stick, and moving along a path.
WMCF builds on earlier books by Lakoff (1987) and Lakoff and Johnson (1980, 1999), which analyze such concepts of metaphor
Metaphor
A metaphor is a literary figure of speech that uses an image, story or tangible thing to represent a less tangible thing or some intangible quality or idea; e.g., "Her eyes were glistening jewels." Metaphor may also be used for any rhetorical figures of speech that achieve their effects via...
and image schemata from second-generation cognitive science
Cognitive science
Cognitive science is the interdisciplinary scientific study of mind and its processes. It examines what cognition is, what it does and how it works. It includes research on how information is processed , represented, and transformed in behaviour, nervous system or machine...
. Some of the riches of these earlier books, such as the interesting technical ideas in Lakoff (1987), are absent from WMCF.
Lakoff and Núñez hold that mathematics results from the human cognitive apparatus and must therefore be understood in cognitive terms. WMCF advocates (and includes some examples of) a cognitive idea analysis of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
which analyzes mathematical ideas in terms of the human experiences, metaphors, generalizations, and other cognitive mechanisms giving rise to them. A standard mathematical education does not develop such idea analysis techniques because it does not pursue considerations of A) what structures of the mind allow it to do mathematics or B) the philosophy of mathematics
Philosophy of mathematics
The philosophy of mathematics is the branch of philosophy that studies the philosophical assumptions, foundations, and implications of mathematics. The aim of the philosophy of mathematics is to provide an account of the nature and methodology of mathematics and to understand the place of...
.
Lakoff and Núñez start by reviewing the psychological literature, concluding that human beings appear to have an innate ability, called subitizing, to count, add, and subtract up to about 4 or 5. They document this conclusion by reviewing the literature, published in recent decades, describing experiments with infant subjects. For example, infants quickly become excited or curious when presented with "impossible" situations, such as having three toys appear when only two were initially present.
The authors argue that mathematics goes far beyond this very elementary level due to a large number of metaphor
Metaphor
A metaphor is a literary figure of speech that uses an image, story or tangible thing to represent a less tangible thing or some intangible quality or idea; e.g., "Her eyes were glistening jewels." Metaphor may also be used for any rhetorical figures of speech that achieve their effects via...
ical constructions. For example, they argue that the Pythagorean
Pythagoreanism
Pythagoreanism was the system of esoteric and metaphysical beliefs held by Pythagoras and his followers, the Pythagoreans, who were considerably influenced by mathematics. Pythagoreanism originated in the 5th century BCE and greatly influenced Platonism...
position that all is number, and the associated crisis of confidence that came about with the discovery of the irrationality of the square root of two, arises solely from a metaphorical relation between the length of the diagonal of a square, and the possible numbers of objects.
Much of WMCF deals with the important concepts of infinity
Infinity
Infinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...
and of limit processes, seeking to explain how finite humans living in a finite world could ultimately conceive of the actual infinite. Thus much of WMCF is, in effect, a study of the epistemological foundations of the calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
. Lakoff and Núñez conclude that while the potential infinite is not metaphorical, the actual infinite is. Moreover, they deem all manifestations of actual infinity to be instances of what they call the "Basic Metaphor of Infinity", as represented by the ever-increasing sequence 1, 2, 3, ...
WMCF emphatically rejects the Platonistic
Platonism
Platonism is the philosophy of Plato or the name of other philosophical systems considered closely derived from it. In a narrower sense the term might indicate the doctrine of Platonic realism...
philosophy of mathematics
Philosophy of mathematics
The philosophy of mathematics is the branch of philosophy that studies the philosophical assumptions, foundations, and implications of mathematics. The aim of the philosophy of mathematics is to provide an account of the nature and methodology of mathematics and to understand the place of...
. They emphasize that all we know and can ever know is human mathematics, the mathematics arising from the human intellect. The question of whether there is a "transcendent" mathematics independent of human thought is a meaningless question. That is like asking if colors are transcendent of human thought- colors are only varying wavelengths of light, it is our interpretation of physical stimuli that make them colors.
WMCF (p. 81) likewise criticizes the emphasis mathematicians place on the concept of closure
Closure (mathematics)
In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
. Lakoff and Núñez argue that the expectation of closure is an artifact of the human mind's ability to relate fundamentally different concepts via metaphor
Metaphor
A metaphor is a literary figure of speech that uses an image, story or tangible thing to represent a less tangible thing or some intangible quality or idea; e.g., "Her eyes were glistening jewels." Metaphor may also be used for any rhetorical figures of speech that achieve their effects via...
.
WMCF concerns itself mainly with proposing and establishing an alternative view of mathematics, one grounding the field in the realities of human biology and experience. It is not a work of technical mathematics or philosophy. Lakoff and Núñez are not the first to argue that conventional approaches to the philosophy of mathematics are flawed. For example, they do not seem all that familiar with the content of Davis and Hersh (1981), even though WMCF warmly acknowledges Reuben Hersh
Reuben Hersh
Reuben Hersh is an American mathematician and academic, best known for his writings on the nature, practice, and social impact of mathematics. This work challenges and complements mainstream philosophy of mathematics.After receiving a B.A...
's support.
Lakoff and Núñez cite Saunders MacLane (the inventor, with Samuel Eilenberg
Samuel Eilenberg
Samuel Eilenberg was a Polish and American mathematician of Jewish descent. He was born in Warsaw, Russian Empire and died in New York City, USA, where he had spent much of his career as a professor at Columbia University.He earned his Ph.D. from University of Warsaw in 1936. His thesis advisor...
, of category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
) in support of their position. MacLane (1986), an overview of mathematics intended for philosophers, proposes that mathematical concepts are ultimately grounded in ordinary human activities, mostly interactions with the physical world. See From Action to Mathematics per Mac Lane.
Educators have taken some interest in what WMCF suggests about how mathematics is learned, and why students find some elementary concepts more difficult than others.
Examples of mathematical metaphors
Conceptual metaphorConceptual metaphor
In cognitive linguistics, conceptual metaphor, or cognitive metaphor, refers to the understanding of one idea, or conceptual domain, in terms of another, for example, understanding quantity in terms of directionality . A conceptual domain can be any coherent organization of human experience...
s described in WMCF, in addition to the Basic Metaphor of Infinity, include:
- ArithmeticArithmeticArithmetic or arithmetics is the oldest and most elementary branch of mathematics, used by almost everyone, for tasks ranging from simple day-to-day counting to advanced science and business calculations. It involves the study of quantity, especially as the result of combining numbers...
is motion along a path, object collection/construction; - Change is motion;
- Sets are containers, objects;
- ContinuityContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
is gapless; - Mathematical systems have an "essence," namely their axiomAxiomIn traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
atic algebraic structureAlgebraic structureIn abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
; - FunctionFunction (mathematics)In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s are sets of ordered pairOrdered pairIn mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
s, curves in the Cartesian plane; - Geometric figures are objects in space;
- Logical independence is geometric orthogonality;
- NumberNumberA number is a mathematical object used to count and measure. In mathematics, the definition of number has been extended over the years to include such numbers as zero, negative numbers, rational numbers, irrational numbers, and complex numbers....
s are sets, object collections, physical segments, points on a line; - Recurrence is circular.
Mathematical reasoning requires variables
Variable (mathematics)
In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
ranging over some universe of discourse, so that we can reason about generalities rather than merely about particulars. WMCF argues that reasoning with such variables implicitly relies on what it terms the Fundamental Metonymy
Metonymy
Metonymy is a figure of speech used in rhetoric in which a thing or concept is not called by its own name, but by the name of something intimately associated with that thing or concept...
of Algebra.
Example of metaphorical ambiguity
WMCF (p. 151) includes the following example of what the authors term "metaphorical ambiguity." Take the set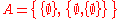 . Then recall two bits of standard terminology from elementary set theory
. Then recall two bits of standard terminology from elementary set theoryNaive set theory
Naive set theory is one of several theories of sets used in the discussion of the foundations of mathematics. The informal content of this naive set theory supports both the aspects of mathematical sets familiar in discrete mathematics , and the everyday usage of set theory concepts in most...
:
- The recursiveRecursively enumerable setIn computability theory, traditionally called recursion theory, a set S of natural numbers is called recursively enumerable, computably enumerable, semidecidable, provable or Turing-recognizable if:...
construction of the ordinal natural numbersOrdinal numberIn set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
, whereby 0 is , and n+1 is n
, and n+1 is n  {n}.
{n}. - The ordered pairOrdered pairIn mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
(a,b), defined as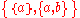 .
.
By (1), A is the set {1,2}. But (1) and (2) together say that A is also the ordered pair (0,1). Both statements cannot be correct; the ordered pair
Ordered pair
In mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
(0,1) and the unordered pair {1,2} are fully distinct concepts. Lakoff and Johnson (1999) term this situation "metaphorically ambiguous." This simple example calls into question any Platonistic
Platonism
Platonism is the philosophy of Plato or the name of other philosophical systems considered closely derived from it. In a narrower sense the term might indicate the doctrine of Platonic realism...
foundations for mathematics.
While (1) and (2) above are admittedly canonical, especially within the consensus set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
known as the Zermelo–Fraenkel axiomatization, WMCF does not let on that they are but one of several definitions that have been proposed since the dawning of set theory. For example, Frege, Principia Mathematica
Principia Mathematica
The Principia Mathematica is a three-volume work on the foundations of mathematics, written by Alfred North Whitehead and Bertrand Russell and published in 1910, 1912, and 1913...
, and New Foundations
New Foundations
In mathematical logic, New Foundations is an axiomatic set theory, conceived by Willard Van Orman Quine as a simplification of the theory of types of Principia Mathematica. Quine first proposed NF in a 1937 article titled "New Foundations for Mathematical Logic"; hence the name...
(a body of axiomatic set theory begun by Quine
Willard Van Orman Quine
Willard Van Orman Quine was an American philosopher and logician in the analytic tradition...
in 1937) define cardinals
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
and ordinals
Ordinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
as equivalence classes under the relations
Relation (mathematics)
In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...
of equinumerosity
Equinumerosity
In mathematics, two sets are equinumerous if they have the same cardinality, i.e., if there exists a bijection f : A → B for sets A and B. This is usually denoted A \approx B \, or A \sim B....
and similarity
Ordinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
, so that this conundrum does not arise. In Quinian set theory, A is simply an instance of the number 2. For technical reasons, defining the ordered pair as in (2) above is awkward in Quinian set theory. Two solutions have been proposed:
- A variant set-theoretic definition of the ordered pair more complicated than the usual one;
- Taking ordered pairs as primitive.
Criticism
In set theories such as Zermelo–FraenkelZermelo–Fraenkel set theory
In mathematics, Zermelo–Fraenkel set theory with the axiom of choice, named after mathematicians Ernst Zermelo and Abraham Fraenkel and commonly abbreviated ZFC, is one of several axiomatic systems that were proposed in the early twentieth century to formulate a theory of sets without the paradoxes...
one can indeed have {1,2} = (0,1), as these are two different symbols denoting the same object. The claim that there is an anomaly because these are "fully distinct concepts" is on the one hand not a clear scientific statement, and on the other hand, is on par with such statements as: ""The positive real solution of
 " and "
" and " " cannot be equal because they are fully distinct concepts.".
" cannot be equal because they are fully distinct concepts.".The apparent anomaly stems from the fact that Lakoff and Núñez identify mathematical objects with their various particular realizations. There are several equivalent definitions of ordered pair, and most mathematicians do not identify the ordered pair with just one of these definitions (since this would be an arbitrary and artificial choice), but view the definitions as equivalent models or realizations of the same underlying object. The existence of several different but equivalent constructions of certain mathematical objects supports the platonistic view that the mathematical objects exist beyond their various linguistical, symbolical, or conceptual representations.
As an example, many mathematicians would favour a definition of ordered pair in terms of category theory where the object in question is defined in terms of a characteristic universal property and then shown to be unique up to unique isomorphism (this was recently mentioned in an article on mathematical platonism by David Mumford).
The above discussion is meant to explain that the most natural and fruitful approach in mathematics is to view a mathematical object as having potentially several different but equivalent realizations. On the other hand, the object is not identified with just one of these realizations. This suggests that the intuitionistic idea that mathematical objects exist only as specific mental constructions, or the idea of Lakoff and Núñez that mathematical objects exist only as particular instances of concepts/metaphors in our embodied brains, is an inadequate philosophical basis to account for the experience and de facto research methods of working mathematicians. Perhaps this is a reason why these ideas have been met with comparatively little interest by the mathematical community.
The Romance of Mathematics
The "Romance of Mathematics" is WMCFs light-hearted term for a perennial philosophical viewpoint about mathematics the authors describe, then dismiss as an intellectual myth:- Mathematics is transcendent, namely it exists independently of human beings, and structures our actual physical universeUniverseThe Universe is commonly defined as the totality of everything that exists, including all matter and energy, the planets, stars, galaxies, and the contents of intergalactic space. Definitions and usage vary and similar terms include the cosmos, the world and nature...
and any possible universe. Mathematics is the language of nature, and is the primary conceptual structure we would have in common with extraterrestrial aliens, if any such there be. - Mathematical proofMathematical proofIn mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
is the gateway to a realm of transcendent truth. - Reasoning is logicLogicIn philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
, and logic is essentially mathematical. Hence mathematics structures all possible reasoning. - Because mathematics exists independently of human beings, and reasoning is essentially mathematical, reason itself is disembodied. Therefore artificial intelligenceArtificial intelligenceArtificial intelligence is the intelligence of machines and the branch of computer science that aims to create it. AI textbooks define the field as "the study and design of intelligent agents" where an intelligent agent is a system that perceives its environment and takes actions that maximize its...
is possible, at least in principle.
It is very much an open question whether WMCF will eventually prove to be the start of a new school in the philosophy of mathematics
Philosophy of mathematics
The philosophy of mathematics is the branch of philosophy that studies the philosophical assumptions, foundations, and implications of mathematics. The aim of the philosophy of mathematics is to provide an account of the nature and methodology of mathematics and to understand the place of...
. Hence the main value of WMCF so far may be a critical one: its critique of Platonism
Platonism
Platonism is the philosophy of Plato or the name of other philosophical systems considered closely derived from it. In a narrower sense the term might indicate the doctrine of Platonic realism...
in mathematics, and the Romance of Mathematics.
Critical response
Many working mathematicians resist the approach and conclusions of Lakoff and Núñez. Reviews by mathematicians of WMCF in professional journals, while often respectful of its focus on conceptual strategies and metaphors as paths for understanding mathematics, have taken exception to some of the WMCFs philosophical arguments on the grounds that mathematical statements have lasting 'objective' meanings. For example, Fermat's last theoremFermat's Last Theorem
In number theory, Fermat's Last Theorem states that no three positive integers a, b, and c can satisfy the equation an + bn = cn for any integer value of n greater than two....
means exactly what it meant when Fermat initially proposed it 1664. Other reviewers have pointed out that multiple conceptual strategies can be employed in connection with the same mathematically defined term, often by the same person (a point that is compatible with the view that we routinely understand the 'same' concept with different metaphors). The metaphor
Metaphor
A metaphor is a literary figure of speech that uses an image, story or tangible thing to represent a less tangible thing or some intangible quality or idea; e.g., "Her eyes were glistening jewels." Metaphor may also be used for any rhetorical figures of speech that achieve their effects via...
and the conceptual strategy are not the same as the formal definition
Definition
A definition is a passage that explains the meaning of a term , or a type of thing. The term to be defined is the definiendum. A term may have many different senses or meanings...
which mathematicians employ. However, WMCF points out that formal definitions are built using words and symbols that have meaning only in terms of human experience.
Critiques of WMCF include the humorous:
- "It's difficult for me to conceive of a metaphor for a real number raised to a complex power, but if there is one, I'd sure like to see it." - Joseph Auslander
and the physically informed:
- "But their analysis leaves at least a couple of questions insufficiently answered. For one thing, the authors ignore the fact that brains not only observe nature, but also are part of nature. Perhaps the math that brains invent takes the form it does because math had a hand in forming the brains in the first place (through the operation of natural laws in constraining the evolution of life). Furthermore, it's one thing to fit equations to aspects of reality that are already known. It's something else for that math to tell of phenomena never previously suspected. When Paul Dirac's equations describing electrons produced more than one solution, he surmised that nature must possess other particles, now known as antimatter. But scientists did not discover such particles until after Dirac's math told him they must exist. If math is a human invention, nature seems to know what was going to be invented."
Mathematicians have also complained that Lakoff and Núñez have misunderstood some basic mathematical notions. The authors reply that the errors found in earlier printings of WMCF are now corrected.
Lakoff made his reputation by linking linguistics
Linguistics
Linguistics is the scientific study of human language. Linguistics can be broadly broken into three categories or subfields of study: language form, language meaning, and language in context....
to cognitive science
Cognitive science
Cognitive science is the interdisciplinary scientific study of mind and its processes. It examines what cognition is, what it does and how it works. It includes research on how information is processed , represented, and transformed in behaviour, nervous system or machine...
and the analysis of metaphor
Metaphor
A metaphor is a literary figure of speech that uses an image, story or tangible thing to represent a less tangible thing or some intangible quality or idea; e.g., "Her eyes were glistening jewels." Metaphor may also be used for any rhetorical figures of speech that achieve their effects via...
. Núñez, educated in Switzerland
Switzerland
Switzerland name of one of the Swiss cantons. ; ; ; or ), in its full name the Swiss Confederation , is a federal republic consisting of 26 cantons, with Bern as the seat of the federal authorities. The country is situated in Western Europe,Or Central Europe depending on the definition....
, is a product of Jean Piaget
Jean Piaget
Jean Piaget was a French-speaking Swiss developmental psychologist and philosopher known for his epistemological studies with children. His theory of cognitive development and epistemological view are together called "genetic epistemology"....
's school of cognitive psychology
Cognitive psychology
Cognitive psychology is a subdiscipline of psychology exploring internal mental processes.It is the study of how people perceive, remember, think, speak, and solve problems.Cognitive psychology differs from previous psychological approaches in two key ways....
as a basis for logic and mathematics. Núñez has thought much about the foundations of real analysis
Real analysis
Real analysis, is a branch of mathematical analysis dealing with the set of real numbers and functions of a real variable. In particular, it deals with the analytic properties of real functions and sequences, including convergence and limits of sequences of real numbers, the calculus of the real...
, the real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
and complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s, and the Basic Metaphor of Infinity. These topics, however, worthy though they be, form part of the superstructure of mathematics. Cognitive science should take more interest in the foundations of mathematics
Foundations of mathematics
Foundations of mathematics is a term sometimes used for certain fields of mathematics, such as mathematical logic, axiomatic set theory, proof theory, model theory, type theory and recursion theory...
. And indeed, the authors do pay a fair bit of attention early on to logic
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
, Boolean algebra and the Zermelo–Fraenkel axioms, even lingering a bit over group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
. But neither author is well-trained in logic
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
(there is no index entry for "quantifier" or "quantification"), the philosophy of set theory, the axiomatic method, metamathematics, and model theory
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
. Nor does WMCF say enough about the derivation of number system
Number system
In mathematics, a 'number system' is a set of numbers, , together with one or more operations, such as addition or multiplication....
s (the Peano axioms
Peano axioms
In mathematical logic, the Peano axioms, also known as the Dedekind–Peano axioms or the Peano postulates, are a set of axioms for the natural numbers presented by the 19th century Italian mathematician Giuseppe Peano...
go unmentioned), abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, equivalence
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
and order relations, mereology
Mereology
In philosophy and mathematical logic, mereology treats parts and the wholes they form...
, topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, and geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
.
Lakoff and Núñez tend to dismiss the negative opinions mathematicians have expressed about WMCF, because their critics do not appreciate the insights of cognitive science. Lakoff and Núñez maintain that their argument can only be understood using the discoveries of recent decades about the way human brains process language and meaning. They argue that any arguments or criticisms that are not grounded in this understanding cannot address the content of the book.
It has been pointed out that it is not at all clear that WMCF establishes that the claim "intelligent alien life would have mathematical ability" is a myth. To do this, it would be required to show that intelligence and mathematical ability are separable, and this has not been done. On Earth, intelligence and mathematical ability seem to go hand in hand in all life-forms, as pointed out by Keith Devlin
Keith Devlin
Keith J. Devlin is a British mathematician and popular science writer. He has lived in the USA since 1987 and has dual American-British citizenship.- Biography :...
among others. The authors of WMCF have not explained how this situation would (or even could) be different anywhere else.
Lakoff and Núñez also appear not to appreciate the extent to which intuitionists and constructivist
Constructivism (mathematics)
In the philosophy of mathematics, constructivism asserts that it is necessary to find a mathematical object to prove that it exists. When one assumes that an object does not exist and derives a contradiction from that assumption, one still has not found the object and therefore not proved its...
s have anticipated their attack on the Romance of (Platonic) Mathematics. Brouwer
Luitzen Egbertus Jan Brouwer
Luitzen Egbertus Jan Brouwer FRS , usually cited as L. E. J. Brouwer but known to his friends as Bertus, was a Dutch mathematician and philosopher, a graduate of the University of Amsterdam, who worked in topology, set theory, measure theory and complex analysis.-Biography:Early in his career,...
, the founder of the intuitionist/constructivist
Constructivism (mathematics)
In the philosophy of mathematics, constructivism asserts that it is necessary to find a mathematical object to prove that it exists. When one assumes that an object does not exist and derives a contradiction from that assumption, one still has not found the object and therefore not proved its...
point of view, wrote "Mathematics is a free construction of the human mind." Hence at least one person writing before Lakoff and Núñez were born concluded that mathematics emerged to serve human purposes and has no existence apart from this fact.
Summing up
WMCF (pp. 378–79) concludes with some key points, a number of which follow. Mathematics arises from our bodies and brains, our everyday experiences, and the concerns of human societies and cultures. It is:- The result of normal adult cognitive capacities, in particular the capacity for conceptual metaphor, and as such is a human universal. The ability to construct conceptual metaphorConceptual metaphorIn cognitive linguistics, conceptual metaphor, or cognitive metaphor, refers to the understanding of one idea, or conceptual domain, in terms of another, for example, understanding quantity in terms of directionality . A conceptual domain can be any coherent organization of human experience...
s is neurologically based, and enables humans to reason about one domain using the language and concepts of another domain. Conceptual metaphorConceptual metaphorIn cognitive linguistics, conceptual metaphor, or cognitive metaphor, refers to the understanding of one idea, or conceptual domain, in terms of another, for example, understanding quantity in terms of directionality . A conceptual domain can be any coherent organization of human experience...
is both what enabled mathematics to grow out of everyday activities, and what enables mathematics to grow by a continual process of analogy and abstraction; - SymbolSymbolA symbol is something which represents an idea, a physical entity or a process but is distinct from it. The purpose of a symbol is to communicate meaning. For example, a red octagon may be a symbol for "STOP". On a map, a picture of a tent might represent a campsite. Numerals are symbols for...
ic, thereby enormously facilitating precise calculation; - Not transcendent, but the result of human evolutionEvolutionEvolution is any change across successive generations in the heritable characteristics of biological populations. Evolutionary processes give rise to diversity at every level of biological organisation, including species, individual organisms and molecules such as DNA and proteins.Life on Earth...
and cultureCultureCulture is a term that has many different inter-related meanings. For example, in 1952, Alfred Kroeber and Clyde Kluckhohn compiled a list of 164 definitions of "culture" in Culture: A Critical Review of Concepts and Definitions...
, to which it owes its effectiveness. The connection between mathematical ideas and our experience of the world occurs within human minds; - A system of human concepts making extraordinary use of the ordinary tools of human cognition;
- An open-ended creation of human beings, who remain responsible for maintaining and extending it;
- One of the greatest products of the collective human imagination, and a magnificent example of the beauty, richness, complexity, diversity, and importance of human ideas.
The cognitive approach to formal system
Formal system
In formal logic, a formal system consists of a formal language and a set of inference rules, used to derive an expression from one or more other premises that are antecedently supposed or derived . The axioms and rules may be called a deductive apparatus...
s, as described and implemented in WMCF, need not be confined to mathematics, but should also prove fruitful when applied to formal logic, and to formal philosophy such as Edward Zalta's theory of abstract objects. Lakoff and Johnson (1999) fruitfully employ the cognitive approach to rethink a good deal of the philosophy of mind
Philosophy of mind
Philosophy of mind is a branch of philosophy that studies the nature of the mind, mental events, mental functions, mental properties, consciousness and their relationship to the physical body, particularly the brain. The mind-body problem, i.e...
, epistemology, metaphysics
Metaphysics
Metaphysics is a branch of philosophy concerned with explaining the fundamental nature of being and the world, although the term is not easily defined. Traditionally, metaphysics attempts to answer two basic questions in the broadest possible terms:...
, and the history of ideas
History of ideas
The history of ideas is a field of research in history that deals with the expression, preservation, and change of human ideas over time. The history of ideas is a sister-discipline to, or a particular approach within, intellectual history...
.
See also
- Abstract objectAbstract objectAn abstract object is an object which does not exist at any particular time or place, but rather exists as a type of thing . In philosophy, an important distinction is whether an object is considered abstract or concrete. Abstract objects are sometimes called abstracta An abstract object is an...
- Cognitive scienceCognitive scienceCognitive science is the interdisciplinary scientific study of mind and its processes. It examines what cognition is, what it does and how it works. It includes research on how information is processed , represented, and transformed in behaviour, nervous system or machine...
- Cognitive science of mathematics
- Philosophy of mathematicsPhilosophy of mathematicsThe philosophy of mathematics is the branch of philosophy that studies the philosophical assumptions, foundations, and implications of mathematics. The aim of the philosophy of mathematics is to provide an account of the nature and methodology of mathematics and to understand the place of...
- Embodied philosophy
- From Action to Mathematics per Mac Lane
- MetaphorMetaphorA metaphor is a literary figure of speech that uses an image, story or tangible thing to represent a less tangible thing or some intangible quality or idea; e.g., "Her eyes were glistening jewels." Metaphor may also be used for any rhetorical figures of speech that achieve their effects via...
- Conceptual metaphorConceptual metaphorIn cognitive linguistics, conceptual metaphor, or cognitive metaphor, refers to the understanding of one idea, or conceptual domain, in terms of another, for example, understanding quantity in terms of directionality . A conceptual domain can be any coherent organization of human experience...
- The Unreasonable Effectiveness of Mathematics in the Natural SciencesThe Unreasonable Effectiveness of Mathematics in the Natural SciencesThe Unreasonable Effectiveness of Mathematics in the Natural Sciences is the title of an article published in 1960 by the physicist Eugene Wigner...
- Foundations of mathematicsFoundations of mathematicsFoundations of mathematics is a term sometimes used for certain fields of mathematics, such as mathematical logic, axiomatic set theory, proof theory, model theory, type theory and recursion theory...
External links
- WMCF web site.
- Reviews of WMCF.
- Joseph Auslander in American Scientist;
- Bonnie Gold in MAA.
- Lakoff's response to Gold's MAA review.

