
Recursively enumerable set
Encyclopedia
In computability theory
, traditionally called recursion theory, a set S of natural numbers is called recursively enumerable, computably enumerable, semidecidable, provable or Turing-recognizable if:
Or, equivalently,
The first condition suggests why the term semidecidable is sometimes used; the second suggests why computably enumerable is used. The abbreviations r.e. and c.e. are often used, even in print, instead of the full phrase.
In computational complexity theory
, the complexity class
containing all recursively enumerable sets is RE
. In recursion theory
, the lattice
of r.e. sets under inclusion is denoted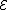 .
.
is exactly S, meaning that the function is defined if and only if its input is a member of S.
The definition can be extended to an arbitrary countable set A by using Gödel number
s to represent elements of the set and declaring a subset of A to be recursively enumerable if the set of corresponding Gödel numbers is recursively enumerable.
Computability theory
Computability theory, also called recursion theory, is a branch of mathematical logic that originated in the 1930s with the study of computable functions and Turing degrees. The field has grown to include the study of generalized computability and definability...
, traditionally called recursion theory, a set S of natural numbers is called recursively enumerable, computably enumerable, semidecidable, provable or Turing-recognizable if:
- There is an algorithmAlgorithmIn mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
such that the set of input numbers for which the algorithm halts is exactly the set of numbers in S.
Or, equivalently,
- There is an algorithm that enumeratesEnumerationIn mathematics and theoretical computer science, the broadest and most abstract definition of an enumeration of a set is an exact listing of all of its elements . The restrictions imposed on the type of list used depend on the branch of mathematics and the context in which one is working...
the members of S. That means that its output is simply a list of the members of S: s1, s2, s3, ... . If necessary, this algorithm may run forever.
The first condition suggests why the term semidecidable is sometimes used; the second suggests why computably enumerable is used. The abbreviations r.e. and c.e. are often used, even in print, instead of the full phrase.
In computational complexity theory
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
, the complexity class
Complexity class
In computational complexity theory, a complexity class is a set of problems of related resource-based complexity. A typical complexity class has a definition of the form:...
containing all recursively enumerable sets is RE
RE (complexity)
In computability theory and computational complexity theory, RE is the class of decision problems for which a 'yes' answer can be verified by a Turing machine in a finite amount of time. Informally, it means that if the answer is 'yes', then there is some procedure which takes finite time to...
. In recursion theory
Recursion theory
Computability theory, also called recursion theory, is a branch of mathematical logic that originated in the 1930s with the study of computable functions and Turing degrees. The field has grown to include the study of generalized computability and definability...
, the lattice
Lattice (order)
In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
of r.e. sets under inclusion is denoted
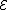 .
.Formal definition
A set S of natural numbers is called recursively enumerable if there is a partial recursive function (synonymously, a partial computable function) whose domainDomain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
is exactly S, meaning that the function is defined if and only if its input is a member of S.
The definition can be extended to an arbitrary countable set A by using Gödel number
Gödel number
In mathematical logic, a Gödel numbering is a function that assigns to each symbol and well-formed formula of some formal language a unique natural number, called its Gödel number. The concept was famously used by Kurt Gödel for the proof of his incompleteness theorems...
s to represent elements of the set and declaring a subset of A to be recursively enumerable if the set of corresponding Gödel numbers is recursively enumerable.
Equivalent formulations
The following are all equivalent properties of a set S of natural numbers:- Semidecidability:
- The set S is recursively enumerable. That is, S is the domain (co-range) of a partial recursive function.
- There is a partial recursive function f such that:
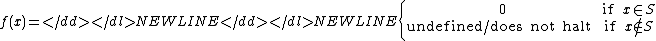
- Enumerability:
- The set S is the range of a partial recursive function.
- The set S is the range of a total recursive function or empty. If S is infinite, the function can be chosen to be injective.
- The set S is the range of a primitive recursive functionPrimitive recursive functionThe primitive recursive functions are defined using primitive recursion and composition as central operations and are a strict subset of the total µ-recursive functions...
or empty. Even if S is infinite, repetition of values may be necessary in this case.
- Diophantine:
- There is a polynomial p with integer coefficients and variables x, a, b, c, d, e, f, g, h, i ranging over the natural numbers such that
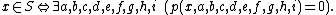
- There is a polynomial from the integers to the integers such that the set S contains exactly the non-negative numbers in its range.
The equivalence of semidecidability and enumerability can be obtained by the technique of dovetailingDovetailing (computer science)Dovetailing in algorithm design, is a technique that interleaves different computations, performing them essentially simultaneously. Algorithms that use dovetailing are sometimes referred to as dovetailers....
.
The Diophantine characterizations of a recursively enumerable set, while not as straightforward or intuitive as the first definitions, were found by Yuri MatiyasevichYuri MatiyasevichYuri Vladimirovich Matiyasevich, is a Russian mathematician and computer scientist. He is best known for his negative solution of Hilbert's tenth problem, presented in his doctoral thesis, at LOMI .- Biography :* In 1962-1963 studied at Saint Petersburg Lyceum 239...
as part of the negative solution to Hilbert's Tenth ProblemHilbert's tenth problemHilbert's tenth problem is the tenth on the list of Hilbert's problems of 1900. Its statement is as follows:Given a Diophantine equation with any number of unknown quantities and with rational integral numerical coefficients: To devise a process according to which it can be determined in a finite...
. Diophantine sets predate recursion theory and are therefore historically the first way to describe these sets (although this equivalence was only remarked more than three decades after the introduction of recursively enumerable sets).
The number of bound variables in the above definition of the Diophantine setDiophantine setIn mathematics, a Diophantine equation is an equation of the form P=0 where P is a polynomial with integer coefficients...
is the best known so far; it might be that a lower number can be used to define all diophantine sets.
Examples
- Every recursive setRecursive setIn computability theory, a set of natural numbers is called recursive, computable or decidable if there is an algorithm which terminates after a finite amount of time and correctly decides whether or not a given number belongs to the set....
is recursively enumerable, but it is not true that every recursively enumerable set is recursive. - A recursively enumerable languageRecursively enumerable languageIn mathematics, logic and computer science, a recursively enumerable language is a type of formal language which is also called partially decidable or Turing-acceptable. It is known as a type-0 language in the Chomsky hierarchy of formal languages...
is a recursively enumerable subset of a formal languageFormal languageA formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
. - The set of all provable sentences in an effectively presented axiomatic system is a recursively enumerable set.
- Matiyasevich's theorem states that every recursively enumerable set is a Diophantine setDiophantine setIn mathematics, a Diophantine equation is an equation of the form P=0 where P is a polynomial with integer coefficients...
(the converse is trivially true). - The simple setSimple setIn recursion theory a subset of the natural numbers is called a simple set if it is recursively enumerable, but every infinite subset of its complement fails to be enumerated recursively...
s are recursively enumerable but not recursive. - The creative sets are recursively enumerable but not recursive.
- Any productive setProductive setIn computability theory, productive sets and creative sets are types of sets of natural numbers that have important applications in mathematical logic...
is not recursively enumerable. - Given a Gödel numbering
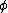 of the computable functions, the set
of the computable functions, the set 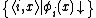 (where
(where 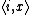 is the Cantor pairing function and
is the Cantor pairing function and 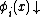 indicates
indicates 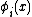 is defined) is recursively enumerable. This set encodes the halting problemHalting problemIn computability theory, the halting problem can be stated as follows: Given a description of a computer program, decide whether the program finishes running or continues to run forever...
is defined) is recursively enumerable. This set encodes the halting problemHalting problemIn computability theory, the halting problem can be stated as follows: Given a description of a computer program, decide whether the program finishes running or continues to run forever...
as it describes the input parameters for which each Turing machineTuring machineA Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
halts. - Given a Gödel numbering
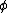 of the computable functions, the set
of the computable functions, the set 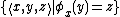 is recursively enumerable. This set encodes the problem of deciding a function value.
is recursively enumerable. This set encodes the problem of deciding a function value. - Given a partial function f from the natural numbers into the natural numbers, f is a partial recursive function if and only if the graph of f, that is, the set of all pairs
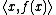 such that f(x) is defined, is recursively enumerable.
such that f(x) is defined, is recursively enumerable.
Properties
If A and B are recursively enumerable sets then A ∩ B, A ∪ B and A × B (with the ordered pair of natural numbers mapped to a single natural number with the Cantor pairing function) are recursively enumerable sets. The preimage of a recursively enumerable set under a partial recursive function is a recursively enumerable set.
A set is recursively enumerable if and only if it is at level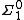 of the arithmetical hierarchyArithmetical hierarchyIn mathematical logic, the arithmetical hierarchy, arithmetic hierarchy or Kleene-Mostowski hierarchy classifies certain sets based on the complexity of formulas that define them...
of the arithmetical hierarchyArithmetical hierarchyIn mathematical logic, the arithmetical hierarchy, arithmetic hierarchy or Kleene-Mostowski hierarchy classifies certain sets based on the complexity of formulas that define them...
.
A set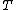 is called co-recursively enumerable or co-r.e. if its complementComplement (set theory)In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
is called co-recursively enumerable or co-r.e. if its complementComplement (set theory)In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
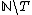 is recursively enumerable. Equivalently, a set is co-r.e. if and only if it is at level
is recursively enumerable. Equivalently, a set is co-r.e. if and only if it is at level 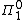 of the arithmetical hierarchy.
of the arithmetical hierarchy.
A set A is recursiveRecursive setIn computability theory, a set of natural numbers is called recursive, computable or decidable if there is an algorithm which terminates after a finite amount of time and correctly decides whether or not a given number belongs to the set....
(synonym: computable) if and only if both A and the complement of A are recursively enumerable. A set is recursive if and only if it is either the range of an increasing total recursive function or finite.
Some pairs of recursively enumerable sets are effectively separable and some are not.
Remarks
According to the Church-Turing thesis, any effectively calculable function is calculable by a Turing machineTuring machineA Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
, and thus a set S is recursively enumerable if and only if there is some algorithmAlgorithmIn mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
which yields an enumeration of S. This cannot be taken as a formal definition, however, because the Church-Turing thesis is an informal conjecture rather than a formal axiom.
The definition of a recursively enumerable set as the domain of a partial function, rather than the range of a total recursive function, is common in contemporary texts. This choice is motivated by the fact that in generalized recursion theories, such as α-recursion theoryAlpha recursion theoryIn recursion theory, α recursion theory is a generalisation of recursion theory to subsets of admissible ordinals \alpha. An admissible ordinal is closed under \Sigma_1 functions. Admissible ordinals are models of Kripke–Platek set theory. In what follows \alpha is considered to be fixed.The...
, the definition corresponding to domains has been found to be more natural. Other texts use the definition in terms of enumerations, which is equivalent for recursively enumerable sets.- Enumerability:

