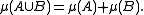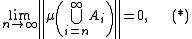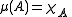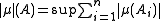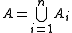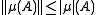Vector measure
Encyclopedia
In mathematics
, a vector measure is a function
defined on a family of sets
and taking vector
values satisfying certain properties. It is a generalization of the concept of measure
, which takes nonnegative real
values only.
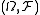 and a Banach space
and a Banach space
 , a finitely additive vector measure (or measure, for short) is a function
, a finitely additive vector measure (or measure, for short) is a function  such that for any two disjoint sets
such that for any two disjoint sets 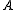 and
and 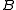 in
in  one has
one has
A vector measure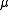 is called countably additive if for any sequence
is called countably additive if for any sequence
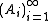 of disjoint sets in
of disjoint sets in 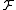 such that their union is in
such that their union is in 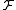 it holds that
it holds that
with the series
on the right-hand side convergent in the norm
of the Banach space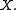
It can be proved that an additive vector measure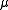 is countably additive if and only if for any sequence
is countably additive if and only if for any sequence 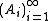 as above one has
as above one has
where is the norm on
is the norm on 
Countably additive vector measures defined on sigma-algebra
s are more general than measures
, signed measure
s, and complex measure
s, which are countably additive functions taking values respectively on the extended interval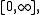 the set of real number
the set of real number
s, and the set of complex number
s.
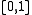 together with the family
together with the family 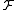 of all Lebesgue measurable sets contained in this interval. For any such set
of all Lebesgue measurable sets contained in this interval. For any such set 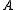 , define
, define
where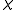 is the indicator function of
is the indicator function of 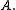 Depending on where
Depending on where 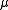 is declared to take values, we get two different outcomes.
is declared to take values, we get two different outcomes.
Both of these statements follow quite easily from the criterion (*) stated above.
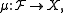 the variation
the variation 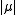 of
of  is defined as
is defined as
where the supremum
is taken over all the partitions
of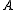 into a finite number of disjoint sets, for all
into a finite number of disjoint sets, for all 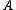 in
in 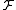 . Here,
. Here,  is the norm on
is the norm on 
The variation of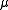 is a finitely additive function taking values in
is a finitely additive function taking values in 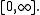 It holds that
It holds that
for any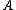 in
in 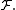 If
If 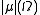 is finite, the measure
is finite, the measure 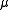 is said to be of bounded variation. One can prove that if
is said to be of bounded variation. One can prove that if 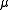 is a vector measure of bounded variation, then
is a vector measure of bounded variation, then  is countably additive if and only if
is countably additive if and only if 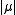 is countably additive.
is countably additive.
's theorem states that the range of a (non-atomic
) vector measure is closed
and convex
. In fact, the range of a non-atomic vector measure is a zonoid (the closed and convex set that is the limit of a convergent sequence of zonotopes). It is used in economics
,
, and in statistical theory
.
Lyapunov's theorem has been proved by using the Shapley–Folkman lemma
, which has been viewed as a discrete
analogue of Lyapunov's theorem;
the Shapley–Folkman lemma has been called a discrete analogue of Lyapunov's theorem.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a vector measure is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
defined on a family of sets
Family of sets
In set theory and related branches of mathematics, a collection F of subsets of a given set S is called a family of subsets of S, or a family of sets over S. More generally, a collection of any sets whatsoever is called a family of sets...
and taking vector
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
values satisfying certain properties. It is a generalization of the concept of measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
, which takes nonnegative real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
values only.
Definitions and first consequences
Given a field of sets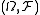 and a Banach space
and a Banach spaceBanach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
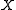 , a finitely additive vector measure (or measure, for short) is a function
, a finitely additive vector measure (or measure, for short) is a function  such that for any two disjoint sets
such that for any two disjoint sets 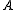 and
and 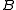 in
in  one has
one hasA vector measure
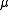 is called countably additive if for any sequence
is called countably additive if for any sequenceSequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
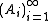 of disjoint sets in
of disjoint sets in 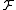 such that their union is in
such that their union is in 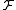 it holds that
it holds thatwith the series
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
on the right-hand side convergent in the norm
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
of the Banach space
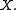
It can be proved that an additive vector measure
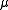 is countably additive if and only if for any sequence
is countably additive if and only if for any sequence 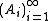 as above one has
as above one haswhere
 is the norm on
is the norm on 
Countably additive vector measures defined on sigma-algebra
Sigma-algebra
In mathematics, a σ-algebra is a technical concept for a collection of sets satisfying certain properties. The main use of σ-algebras is in the definition of measures; specifically, the collection of sets over which a measure is defined is a σ-algebra...
s are more general than measures
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
, signed measure
Signed measure
In mathematics, signed measure is a generalization of the concept of measure by allowing it to have negative values. Some authors may call it a charge, by analogy with electric charge, which is a familiar distribution that takes on positive and negative values.-Definition:There are two slightly...
s, and complex measure
Complex measure
In mathematics, specifically measure theory, a complex measure generalizes the concept of measure by letting it have complex values. In other words, one allows for sets whose size is a complex number.-Definition:...
s, which are countably additive functions taking values respectively on the extended interval
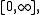 the set of real number
the set of real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, and the set of complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s.
Examples
Consider the field of sets made up of the interval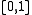 together with the family
together with the family 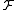 of all Lebesgue measurable sets contained in this interval. For any such set
of all Lebesgue measurable sets contained in this interval. For any such set  , define
, definewhere
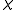 is the indicator function of
is the indicator function of 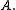 Depending on where
Depending on where 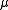 is declared to take values, we get two different outcomes.
is declared to take values, we get two different outcomes.-
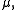 viewed as a function from
viewed as a function from 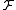 to the Lp spaceLp spaceIn mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
to the Lp spaceLp spaceIn mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
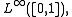 is a vector measure which is not countably-additive.
is a vector measure which is not countably-additive.
-
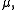 viewed as a function from
viewed as a function from 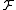 to the Lp space
to the Lp space 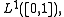 is a countably-additive vector measure.
is a countably-additive vector measure.
Both of these statements follow quite easily from the criterion (*) stated above.
The variation of a vector measure
Given a vector measure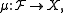 the variation
the variation 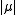 of
of  is defined as
is defined aswhere the supremum
Supremum
In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
is taken over all the partitions
Partition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
of
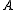 into a finite number of disjoint sets, for all
into a finite number of disjoint sets, for all 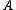 in
in 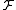 . Here,
. Here,  is the norm on
is the norm on 
The variation of
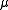 is a finitely additive function taking values in
is a finitely additive function taking values in 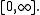 It holds that
It holds thatfor any
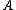 in
in 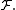 If
If 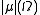 is finite, the measure
is finite, the measure 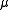 is said to be of bounded variation. One can prove that if
is said to be of bounded variation. One can prove that if 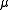 is a vector measure of bounded variation, then
is a vector measure of bounded variation, then  is countably additive if and only if
is countably additive if and only if 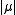 is countably additive.
is countably additive.Lyapunov's theorem
In the theory of vector measures, LyapunovAleksandr Lyapunov
Aleksandr Mikhailovich Lyapunov was a Russian mathematician, mechanician and physicist. His surname is sometimes romanized as Ljapunov, Liapunov or Ljapunow....
's theorem states that the range of a (non-atomic
Atom (measure theory)
In mathematics, more precisely in measure theory, an atom is a measurable set which has positive measure and contains no set of smaller but positive measure...
) vector measure is closed
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
and convex
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
. In fact, the range of a non-atomic vector measure is a zonoid (the closed and convex set that is the limit of a convergent sequence of zonotopes). It is used in economics
Mathematical economics
Mathematical economics is the application of mathematical methods to represent economic theories and analyze problems posed in economics. It allows formulation and derivation of key relationships in a theory with clarity, generality, rigor, and simplicity...
,
in ("bang–bang") control theory
Control theory
Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
, and in statistical theory
Statistical theory
The theory of statistics provides a basis for the whole range of techniques, in both study design and data analysis, that are used within applications of statistics. The theory covers approaches to statistical-decision problems and to statistical inference, and the actions and deductions that...
.
Lyapunov's theorem has been proved by using the Shapley–Folkman lemma
Shapley–Folkman lemma
In geometry and economics, the Shapley–Folkman lemma describes the Minkowski addition of sets in a vector space. Minkowski addition is defined as the addition of the sets' members: for example, adding the set consisting of the integers zero and one to itself yields the set consisting of...
, which has been viewed as a discrete
Discretization
In mathematics, discretization concerns the process of transferring continuous models and equations into discrete counterparts. This process is usually carried out as a first step toward making them suitable for numerical evaluation and implementation on digital computers...
analogue of Lyapunov's theorem;
the Shapley–Folkman lemma has been called a discrete analogue of Lyapunov's theorem.
Books
}}- Kluvánek, I.Igor KluvánekIgor Kluvánek was a Slovak-Australian mathematician.-Academic career:Igor Kluvánek obtained his first degree in electrical engineering from the Slovak Polytechnic University, Bratislava, in 1953. His first appointment was in the Department of Mathematics of the same institution. At the same time...
, Knowles, G, Vector Measures and Control Systems, North-Holland Mathematics Studies 20, Amsterdam, 1976.