
Vector flow
Encyclopedia
In mathematics
, the vector flow refers to a set of closely related concepts of the flow
determined by a vector field
. These appear in a number of different contexts, including differential topology
, Riemannian geometry
and Lie group
theory. These related concepts are explored in a spectrum of articles:
Let V be a smooth vector field on a smooth manifold M. There is a unique maximal flow D → M whose infinitesimal generator is V. Here D ⊆ R × M is the flow domain. For each p ∈ M the map Dp → M is the unique maximal integral curve
of V starting at p.
A global flow is one whose flow domain is all of R × M. Global flows define smooth actions of R on M. A vector field is complete if it generates a global flow. Every vector field on a compact manifold without boundary is complete.
The exponential map
is defined as exp(X) = γ(1) where γ : I → M is the unique geodesic passing through p at 0 and whose tangent vector at 0 is X. Here I is the maximal open interval of R for which the geodesic is defined.
Let M be a pseudo-Riemannian manifold (or any manifold with an affine connection
) and let p be a point in M. Then for every V in TpM there exists a unique geodesic γ : I → M for which γ(0) = p and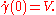 Let Dp be the subset of TpM for which 1 lies in I.
Let Dp be the subset of TpM for which 1 lies in I.
Every left-invariant vector field on a Lie group is complete. The integral curve
starting at the identity is a one-parameter subgroup of G. There are one-to-one correspondences
Let G be a Lie group and g its Lie algebra. The exponential map
is a map exp : g → G given by exp(X) = γ(1) where γ is the integral curve starting at the identity in G generated by X.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the vector flow refers to a set of closely related concepts of the flow
Flow (mathematics)
In mathematics, a flow formalizes the idea of the motion of particles in a fluid. Flows are ubiquitous in science, including engineering and physics. The notion of flow is basic to the study of ordinary differential equations. Informally, a flow may be viewed as a continuous motion of points over...
determined by a vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
. These appear in a number of different contexts, including differential topology
Differential topology
In mathematics, differential topology is the field dealing with differentiable functions on differentiable manifolds. It is closely related to differential geometry and together they make up the geometric theory of differentiable manifolds.- Description :...
, Riemannian geometry
Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
and Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
theory. These related concepts are explored in a spectrum of articles:
- exponential mapExponential mapIn differential geometry, the exponential map is a generalization of the ordinary exponential function of mathematical analysis to all differentiable manifolds with an affine connection....
- matrix exponentialMatrix exponentialIn mathematics, the matrix exponential is a matrix function on square matrices analogous to the ordinary exponential function. Abstractly, the matrix exponential gives the connection between a matrix Lie algebra and the corresponding Lie group....
- exponential functionExponential functionIn mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
- matrix exponential
- infinitesimal generator (→ Lie group)
- integral curveIntegral curveIn mathematics, an integral curve is a parametric curve that represents a specific solution to an ordinary differential equation or system of equations...
(→ vector field) - one-parameter subgroup
- flow (geometry)
- geodesic flow
- Hamiltonian flow
- Ricci flowRicci flowIn differential geometry, the Ricci flow is an intrinsic geometric flow. It is a process that deforms the metric of a Riemannian manifold in a way formally analogous to the diffusion of heat, smoothing out irregularities in the metric....
- Anosov flow
- injectivity radius (→ glossary)
Vector flow in differential topology
Relevant concepts: (flow, infinitesimal generator, integral curve, complete vector field)Let V be a smooth vector field on a smooth manifold M. There is a unique maximal flow D → M whose infinitesimal generator is V. Here D ⊆ R × M is the flow domain. For each p ∈ M the map Dp → M is the unique maximal integral curve
Integral curve
In mathematics, an integral curve is a parametric curve that represents a specific solution to an ordinary differential equation or system of equations...
of V starting at p.
A global flow is one whose flow domain is all of R × M. Global flows define smooth actions of R on M. A vector field is complete if it generates a global flow. Every vector field on a compact manifold without boundary is complete.
Vector flow in Riemannian geometry
Relevant concepts: (geodesic, exponential map, injectivity radius)The exponential map
- exp : TpM → M
is defined as exp(X) = γ(1) where γ : I → M is the unique geodesic passing through p at 0 and whose tangent vector at 0 is X. Here I is the maximal open interval of R for which the geodesic is defined.
Let M be a pseudo-Riemannian manifold (or any manifold with an affine connection
Affine connection
In the branch of mathematics called differential geometry, an affine connection is a geometrical object on a smooth manifold which connects nearby tangent spaces, and so permits tangent vector fields to be differentiated as if they were functions on the manifold with values in a fixed vector space...
) and let p be a point in M. Then for every V in TpM there exists a unique geodesic γ : I → M for which γ(0) = p and
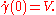 Let Dp be the subset of TpM for which 1 lies in I.
Let Dp be the subset of TpM for which 1 lies in I.Vector flow in Lie group theory
Relevant concepts: (exponential map, infinitesimal generator, one-parameter group)Every left-invariant vector field on a Lie group is complete. The integral curve
Integral curve
In mathematics, an integral curve is a parametric curve that represents a specific solution to an ordinary differential equation or system of equations...
starting at the identity is a one-parameter subgroup of G. There are one-to-one correspondences
- {one-parameter subgroups of G} ⇔ {left-invariant vector fields on G} ⇔ g = TeG.
Let G be a Lie group and g its Lie algebra. The exponential map
Exponential map
In differential geometry, the exponential map is a generalization of the ordinary exponential function of mathematical analysis to all differentiable manifolds with an affine connection....
is a map exp : g → G given by exp(X) = γ(1) where γ is the integral curve starting at the identity in G generated by X.
- The exponential map is smooth.
- For a fixed X, the map t exp(tX) is the one-parameter subgroup of G generated by X.
- The exponential map restricts to a diffeomorphism from some neighborhood of 0 in g to a neighborhood of e in G.
- The image of the exponential map always lies in the connected component of the identity in G.

