
Super vector space
Encyclopedia
In mathematics
, a super vector space is another name for a Z2-graded vector space
, that is, a vector space
over a field
K with a given decomposition
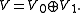
The study of super vector spaces and their generalizations is sometimes called super linear algebra. These objects find their principal application in theoretical physics
where they are used to describe the various algebraic aspects of supersymmetry
.
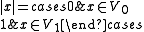
Vectors of parity 0 are called even and those of parity 1 are called odd. Definitions for super vector spaces are often given only in terms of homogeneous elements and then extended to nonhomogeneous elements by linearity.
If V is finite-dimensional and the dimensions of V0 and V1 are p and q respectively, then V is said to have dimension p|q. The standard super coordinate space, denoted Kp|q, is the ordinary coordinate space
Kp+q where the even subspace is spanned by the first p coordinate basis vectors and the odd space is spanned by the last q.
A homogeneous subspace of a super vector space is a linear subspace
that is spanned by homogeneous elements. Homogeneous subspaces are super vector spaces in their own right (with the obvious grading).
For any super vector space V, one can define the parity reversed space ΠV to be the super vector space with the even and odd subspaces interchanged. That is,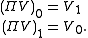
from one super vector space to another is a grade-preserving linear transformation
. A linear transformation f : V → W between super vector spaces is grade preserving if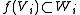
for i = 0 and 1. That is, it maps the even elements of V to even elements of W and odd elements of V to odd elements of W. An isomorphism
of super vector spaces is a bijective homomorphism.
Every linear transformation from one super vector space to another can be written uniquely as the sum of a grade-preserving transformation and a grade-reversing one—that is, a transformation f : V → W such that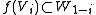
for i = 0 and 1. Declaring the grade-preserving transformations to be even and the grade-reversing ones to be odd gives the space of all linear transformations from V to W the structure of a super vector space.
Note that a grade-reversing transformation from V to W can be regarded as a homomorphism from V to the parity reversed space ΠW.
V* of a super vector space V can be regarded as a super vector space by taking the even functionals to be those that vanish on V1 and the odd functionals to be those that vanish on V0. Equivalently, one can define V* to be the space of linear maps from V to K1|0 (the base field K thought of as a purely even super vector space) with the gradation given in the previous section.
Direct sums of super vector spaces are constructed as in the ungraded case with the grading given by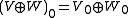
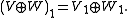
One can also construct tensor products of super vector spaces. Here the additive structure of Z2 comes into play. The underlying space is as in the ungraded case with the grading given by
where the indices are in Z2. Specifically, one has
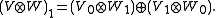
s over a commutative ring
, one may generalize super vector spaces over a field to supermodule
s over a supercommutative algebra
(or ring).
A common construction when working with super vector spaces is to enlarge the field of scalars to a supercommutative Grassmann algebra. Given a field K let
denote the Grassmann algebra generated by N anticommuting odd elements θi. Any super vector space over K can be embedded in a module over R by considering the (graded) tensor product
whose objects are super vector spaces (over a fixed field K) and whose morphism
s are even linear transformations (i.e. the grade preserving ones).
The categorical approach to super linear algebra is to first formulate definitions and theorems regarding ordinary (ungraded) algebraic objects in the language of category theory
and then transfer these directly to the category of super vector spaces. This leads to a treatment of "superobjects" such as superalgebra
s, Lie superalgebra
s, supergroup
s, etc. that is completely analogous to their ungraded counterparts.
The category K-SVect is a monoidal category
with the super tensor product as the monoidal product and the purely even super vector space K1|0 as the unit object. The involutive braiding operator

given by
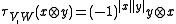
on pure elements, turns K-SVect into a symmetric monoidal category. This commutativity isomorphism encodes the "rule of signs" that is essential to super linear algebra. It effectively says that a minus sign is picked up whenever two odd elements are interchanged. One need not worry about signs in the categorical setting as long as the above operator is used wherever appropriate.
K-SVect is also a closed monoidal category
with the internal Hom object, Hom(V, W), given by the super vector space of all linear maps from V to W. The ordinary Hom set Hom(V, W) is the even subspace therein: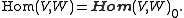
The fact that K-SVect is closed means that the functor –⊗V is left adjoint to the functor Hom(V,–), given a natural bijection: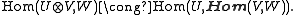
A superalgebra
over K can be described as a super vector space A with a multiplication map
Associativity and the existence of an identity can be expressed with the usual commutative diagrams, so that a unital associative superalgebra over K is a monoid
in the category K-SVect.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a super vector space is another name for a Z2-graded vector space
Graded vector space
In mathematics, a graded vector space is a type of vector space that includes the extra structure of gradation, which is a decomposition of the vector space into a direct sum of vector subspaces.-N-graded vector spaces:...
, that is, a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
K with a given decomposition
Direct sum
In mathematics, one can often define a direct sum of objectsalready known, giving a new one. This is generally the Cartesian product of the underlying sets , together with a suitably defined structure. More abstractly, the direct sum is often, but not always, the coproduct in the category in question...
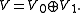
The study of super vector spaces and their generalizations is sometimes called super linear algebra. These objects find their principal application in theoretical physics
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
where they are used to describe the various algebraic aspects of supersymmetry
Supersymmetry
In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...
.
Definitions
Vectors which are elements of either V0 or V1 are said to be homogeneous. The parity of a nonzero homogeneous element, denoted by |x|, is 0 or 1 according to whether it is in V0 or V1.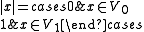
Vectors of parity 0 are called even and those of parity 1 are called odd. Definitions for super vector spaces are often given only in terms of homogeneous elements and then extended to nonhomogeneous elements by linearity.
If V is finite-dimensional and the dimensions of V0 and V1 are p and q respectively, then V is said to have dimension p|q. The standard super coordinate space, denoted Kp|q, is the ordinary coordinate space
Coordinate space
In mathematics, specifically in linear algebra, the coordinate space, Fn, is the prototypical example of an n-dimensional vector space over a field F. It can be defined as the product space of F over a finite index set.-Definition:...
Kp+q where the even subspace is spanned by the first p coordinate basis vectors and the odd space is spanned by the last q.
A homogeneous subspace of a super vector space is a linear subspace
Linear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
that is spanned by homogeneous elements. Homogeneous subspaces are super vector spaces in their own right (with the obvious grading).
For any super vector space V, one can define the parity reversed space ΠV to be the super vector space with the even and odd subspaces interchanged. That is,
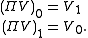
Linear transformations
A homomorphismHomomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
from one super vector space to another is a grade-preserving linear transformation
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
. A linear transformation f : V → W between super vector spaces is grade preserving if
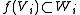
for i = 0 and 1. That is, it maps the even elements of V to even elements of W and odd elements of V to odd elements of W. An isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
of super vector spaces is a bijective homomorphism.
Every linear transformation from one super vector space to another can be written uniquely as the sum of a grade-preserving transformation and a grade-reversing one—that is, a transformation f : V → W such that
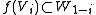
for i = 0 and 1. Declaring the grade-preserving transformations to be even and the grade-reversing ones to be odd gives the space of all linear transformations from V to W the structure of a super vector space.
Note that a grade-reversing transformation from V to W can be regarded as a homomorphism from V to the parity reversed space ΠW.
Operations on super vector spaces
The dual spaceDual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
V* of a super vector space V can be regarded as a super vector space by taking the even functionals to be those that vanish on V1 and the odd functionals to be those that vanish on V0. Equivalently, one can define V* to be the space of linear maps from V to K1|0 (the base field K thought of as a purely even super vector space) with the gradation given in the previous section.
Direct sums of super vector spaces are constructed as in the ungraded case with the grading given by
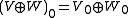
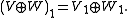
One can also construct tensor products of super vector spaces. Here the additive structure of Z2 comes into play. The underlying space is as in the ungraded case with the grading given by

where the indices are in Z2. Specifically, one has

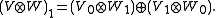
Supermodules
Just as one may generalize vector spaces over a field to moduleModule (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
s over a commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
, one may generalize super vector spaces over a field to supermodule
Supermodule
In mathematics, a supermodule is a Z2-graded module over a superring or superalgebra. Supermodules arise in super linear algebra which is a mathematical framework for studying the concept supersymmetry in theoretical physics....
s over a supercommutative algebra
Supercommutative algebra
In mathematics, a supercommutative algebra is a superalgebra such that for any two homogeneous elements x, y we haveyx = ^In mathematics, a supercommutative algebra is a superalgebra In mathematics, a supercommutative algebra is a superalgebra (i.e. a Z2-graded algebra) such that for any two...
(or ring).
A common construction when working with super vector spaces is to enlarge the field of scalars to a supercommutative Grassmann algebra. Given a field K let

denote the Grassmann algebra generated by N anticommuting odd elements θi. Any super vector space over K can be embedded in a module over R by considering the (graded) tensor product

The category of super vector spaces
The category of super vector spaces, denoted by K-SVect, is the categoryCategory (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
whose objects are super vector spaces (over a fixed field K) and whose morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
s are even linear transformations (i.e. the grade preserving ones).
The categorical approach to super linear algebra is to first formulate definitions and theorems regarding ordinary (ungraded) algebraic objects in the language of category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
and then transfer these directly to the category of super vector spaces. This leads to a treatment of "superobjects" such as superalgebra
Superalgebra
In mathematics and theoretical physics, a superalgebra is a Z2-graded algebra. That is, it is an algebra over a commutative ring or field with a decomposition into "even" and "odd" pieces and a multiplication operator that respects the grading....
s, Lie superalgebra
Lie superalgebra
In mathematics, a Lie superalgebra is a generalisation of a Lie algebra to include a Z2-grading. Lie superalgebras are important in theoretical physics where they are used to describe the mathematics of supersymmetry...
s, supergroup
Supergroup (physics)
The concept of supergroup is a generalization of that of group. In other words, every group is a supergroup but not every supergroup is a group. A supergroup is like a Lie group in that there is a well defined notion of smooth function defined on them....
s, etc. that is completely analogous to their ungraded counterparts.
The category K-SVect is a monoidal category
Monoidal category
In mathematics, a monoidal category is a category C equipped with a bifunctorwhich is associative, up to a natural isomorphism, and an object I which is both a left and right identity for ⊗, again up to a natural isomorphism...
with the super tensor product as the monoidal product and the purely even super vector space K1|0 as the unit object. The involutive braiding operator

given by
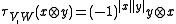
on pure elements, turns K-SVect into a symmetric monoidal category. This commutativity isomorphism encodes the "rule of signs" that is essential to super linear algebra. It effectively says that a minus sign is picked up whenever two odd elements are interchanged. One need not worry about signs in the categorical setting as long as the above operator is used wherever appropriate.
K-SVect is also a closed monoidal category
Closed monoidal category
In mathematics, especially in category theory, aclosed monoidal category is a context where we can take tensor products of objects and also form 'mapping objects'. A classic example is the category of sets, Set, where the tensor product of sets A and B is the usual cartesian product A \times B, and...
with the internal Hom object, Hom(V, W), given by the super vector space of all linear maps from V to W. The ordinary Hom set Hom(V, W) is the even subspace therein:
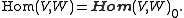
The fact that K-SVect is closed means that the functor –⊗V is left adjoint to the functor Hom(V,–), given a natural bijection:
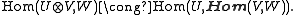
A superalgebra
Superalgebra
In mathematics and theoretical physics, a superalgebra is a Z2-graded algebra. That is, it is an algebra over a commutative ring or field with a decomposition into "even" and "odd" pieces and a multiplication operator that respects the grading....
over K can be described as a super vector space A with a multiplication map

Associativity and the existence of an identity can be expressed with the usual commutative diagrams, so that a unital associative superalgebra over K is a monoid
Monoid (category theory)
In category theory, a monoid in a monoidal category is an object M together with two morphisms* \mu : M\otimes M\to M called multiplication,* and \eta : I\to M called unit,...
in the category K-SVect.

