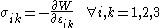Variational inequality
Encyclopedia
In mathematics
, a variational inequality is an inequality involving a functional
, which has to be solved for all the value
of a given variable
, belonging usually to a convex set
. The mathematical theory
of variational inequalities was initially developed to deal with equilibrium problems, precisely the Signorini problem
: in that model problem, the functional involved was obtained as the first variation
of the involved potential energy therefore it has a variational origin, recalled by the name of the general abstract problem. The applicability of the theory has since been expanded to include problems from economics
, finance
, optimization
and game theory
.
, posed by Antonio Signorini
in 1959 and solved by Gaetano Fichera
in 1963, according to the references and : the first papers of the theory were and , . Later on, Guido Stampacchia
proved his generalization to the Lax–Milgram theorem in in order to study the regularity problem for partial differential equation
s and coin
ed the name "variational inequality" for all the problems involving inequalities of this kind. Georges Duvaut encouraged his graduate students to study and expand on Fichera's work, after attending a conference in Brixen
on 1965 where Fichera presented his study of the Signorini problem, as reports: thus the theory become widely known throughout France
. Also in 1965, Stampacchia and Jacques-Louis Lions
extended earlier results of , announcing them in the paper : full proofs of their results appeared later in the paper .
Given a Banach space
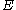 , a subset
, a subset
 of
of 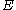 , and a functional
, and a functional
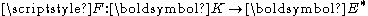 from
from 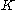 to the dual space
to the dual space
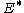 of the space
of the space 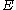 , the variational inequality problem is the problem of solving respect to the variable
, the variational inequality problem is the problem of solving respect to the variable
 belonging to
belonging to 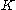 the following inequality:
the following inequality:
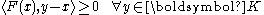
where is the duality pairing
is the duality pairing
.
In general, the variational inequality problem can be formulated on any finite – or infinite-dimension
al Banach space
. The three obvious steps in the study of the problem are the following ones:
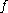 over a closed interval
over a closed interval 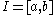 . Let
. Let 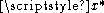 be a point in
be a point in  where the minimum occurs. Three cases can occur:
where the minimum occurs. Three cases can occur:
These necessary conditions can be summarized as the problem of finding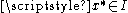 such that
such that
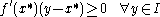
The absolute minimum must be searched between the solutions (if more than one) of the preceding inequality: note that the solution is a real number
, therefore this is a finite dimensional variational inequality.
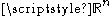 is the following: given a subset
is the following: given a subset
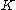 of
of 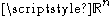 and a mapping
and a mapping
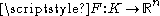 , the finite-dimension
, the finite-dimension
al variational inequality problem associated with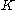 consist of finding a
consist of finding a  -dimensional
-dimensional
vector belonging to
belonging to 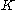 such that
such that
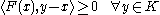
where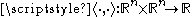 is the standard inner product on the vector space
is the standard inner product on the vector space
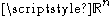 .
.
 In the historical survey , Gaetano Fichera
In the historical survey , Gaetano Fichera
describes the genesis of his solution to the Signorini problem
: the problem consist in finding the elastic equilibrium configuration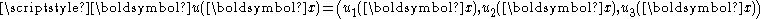 of an anisotropic non-homogeneous elastic body
of an anisotropic non-homogeneous elastic body
that lies in a subset
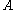 of the three-dimension
of the three-dimension
al euclidean space
whose boundary
is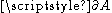 , resting on a rigid
, resting on a rigid
frictionless surface
and subject only to its mass force
s. The solution of the problem exists and is unique (under precise assumptions) in the set of admissible displacements
of the problem exists and is unique (under precise assumptions) in the set of admissible displacements 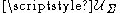 i.e. the set of displacement vectors satisfying the system of ambiguous boundary conditions if and only if
i.e. the set of displacement vectors satisfying the system of ambiguous boundary conditions if and only if

where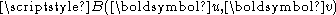 and
and 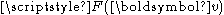 are the following functionals
are the following functionals
, written using the Einstein notation
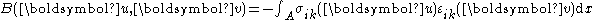
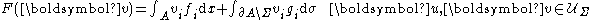
where, for all ,
,
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a variational inequality is an inequality involving a functional
Functional (mathematics)
In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...
, which has to be solved for all the value
Value (mathematics)
In mathematics, value commonly refers to the 'output' of a function. In the most basic case, that of unary, single-valued functions, there is one input and one output .The function f of the example is real-valued, since each and every possible function value is real...
of a given variable
Variable (mathematics)
In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
, belonging usually to a convex set
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
. The mathematical theory
Theory
The English word theory was derived from a technical term in Ancient Greek philosophy. The word theoria, , meant "a looking at, viewing, beholding", and referring to contemplation or speculation, as opposed to action...
of variational inequalities was initially developed to deal with equilibrium problems, precisely the Signorini problem
Signorini problem
The Signorini problem is an elastostatics problem in linear elasticity: it consists in finding the elastic equilibrium configuration of an anisotropic non-homogeneous elastic body, resting on a rigid frictionless surface and subject only to its mass forces...
: in that model problem, the functional involved was obtained as the first variation
First variation
In applied mathematics and the calculus of variations, the first variation of a functional J is defined as the linear functional \delta J mapping the function h to...
of the involved potential energy therefore it has a variational origin, recalled by the name of the general abstract problem. The applicability of the theory has since been expanded to include problems from economics
Economics
Economics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
, finance
Finance
"Finance" is often defined simply as the management of money or “funds” management Modern finance, however, is a family of business activity that includes the origination, marketing, and management of cash and money surrogates through a variety of capital accounts, instruments, and markets created...
, optimization
Optimization (mathematics)
In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
and game theory
Game theory
Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
.
History
The first problem involving a variational inequality was the Signorini problemSignorini problem
The Signorini problem is an elastostatics problem in linear elasticity: it consists in finding the elastic equilibrium configuration of an anisotropic non-homogeneous elastic body, resting on a rigid frictionless surface and subject only to its mass forces...
, posed by Antonio Signorini
Antonio Signorini
- Research activity :His scientific production const of more than 114 works, being papers, monographs and textbooks, 17 of which have been collected in his "Opere Scelte".- Teaching activity :...
in 1959 and solved by Gaetano Fichera
Gaetano Fichera
Gaetano Fichera was an Italian mathematician, working in mathematical analysis, linear elasticity, partial differential equations and several complex variables...
in 1963, according to the references and : the first papers of the theory were and , . Later on, Guido Stampacchia
Guido Stampacchia
Guido Stampacchia was a 20th century mathematician.Stampacchia was born in Naples, Italy. He obtained his high school certification from the Liceo-Ginnasio Giambattista Vico in Naples in classical subjects, although he showed stronger aptitude for mathematics and physics.In 1940 he was admitted to...
proved his generalization to the Lax–Milgram theorem in in order to study the regularity problem for partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s and coin
Coin
A coin is a piece of hard material that is standardized in weight, is produced in large quantities in order to facilitate trade, and primarily can be used as a legal tender token for commerce in the designated country, region, or territory....
ed the name "variational inequality" for all the problems involving inequalities of this kind. Georges Duvaut encouraged his graduate students to study and expand on Fichera's work, after attending a conference in Brixen
Brixen
Brixen is the name of two cities in the Alps:*Brixen, South Tyrol, Italy*Brixen im Thale, Tyrol, AustriaBrixen may also refer to:*Bishopric of Brixen, the former north-Italian state....
on 1965 where Fichera presented his study of the Signorini problem, as reports: thus the theory become widely known throughout France
France
The French Republic , The French Republic , The French Republic , (commonly known as France , is a unitary semi-presidential republic in Western Europe with several overseas territories and islands located on other continents and in the Indian, Pacific, and Atlantic oceans. Metropolitan France...
. Also in 1965, Stampacchia and Jacques-Louis Lions
Jacques-Louis Lions
Jacques-Louis Lions ForMemRS was a French mathematician who made contributions to the theory of partial differential equations and to stochastic control, among other areas. He received the SIAM's John Von Neumann prize in 1986. Lions is listed as an ISI highly cited researcher.-Biography:After...
extended earlier results of , announcing them in the paper : full proofs of their results appeared later in the paper .
Definition
Following , the formal definition of a variational inequality is the following one.Given a Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
 , a subset
, a subsetSubset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
 of
of 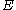 , and a functional
, and a functionalFunctional
Generally, functional refers to something able to fulfill its purpose or function.*Functionalism and Functional form, movements in architectural design*Functional group, certain atomic combinations that occur in various molecules, e.g...
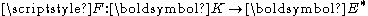 from
from 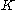 to the dual space
to the dual spaceDual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
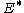 of the space
of the space 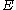 , the variational inequality problem is the problem of solving respect to the variable
, the variational inequality problem is the problem of solving respect to the variableVariable (mathematics)
In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
 belonging to
belonging to 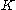 the following inequality:
the following inequality: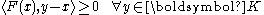
where
 is the duality pairing
is the duality pairingDual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
.
In general, the variational inequality problem can be formulated on any finite – or infinite-dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
. The three obvious steps in the study of the problem are the following ones:
- Prove the existence of a solution: this step implies the mathematical correctness of the problem, showing that there is at least a solution.
- Prove the uniqueness of the given solution: this step implies the physical correctness of the problem, showing that the solution can be used to represent a physical phenomenon. It is a particularly important step since most of the problems modeled by variational inequalities are of physical origin.
- Find the solution.
The problem of finding the minimal value of a real-valued function of real variable
This is a standard example problem, reported by : consider the problem of finding the minimal value of a differentiable functionDifferentiable function
In calculus , a differentiable function is a function whose derivative exists at each point in its domain. The graph of a differentiable function must have a non-vertical tangent line at each point in its domain...
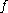 over a closed interval
over a closed interval 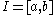 . Let
. Let 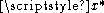 be a point in
be a point in  where the minimum occurs. Three cases can occur:
where the minimum occurs. Three cases can occur:- if
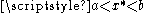 then
then 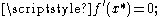
- if
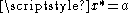 then
then 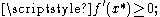
- if
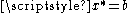 then
then 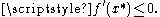
These necessary conditions can be summarized as the problem of finding
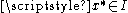 such that
such that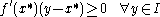
The absolute minimum must be searched between the solutions (if more than one) of the preceding inequality: note that the solution is a real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
, therefore this is a finite dimensional variational inequality.
The general finite dimensional variational inequality
A formulation of the general problem in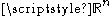 is the following: given a subset
is the following: given a subsetSubset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
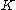 of
of 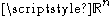 and a mapping
and a mappingMap (mathematics)
In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
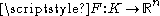 , the finite-dimension
, the finite-dimensionDimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al variational inequality problem associated with
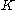 consist of finding a
consist of finding a  -dimensional
-dimensionalDimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
vector
 belonging to
belonging to 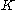 such that
such that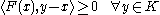
where
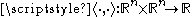 is the standard inner product on the vector space
is the standard inner product on the vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
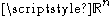 .
.The variational inequality for the Signorini problem

Gaetano Fichera
Gaetano Fichera was an Italian mathematician, working in mathematical analysis, linear elasticity, partial differential equations and several complex variables...
describes the genesis of his solution to the Signorini problem
Signorini problem
The Signorini problem is an elastostatics problem in linear elasticity: it consists in finding the elastic equilibrium configuration of an anisotropic non-homogeneous elastic body, resting on a rigid frictionless surface and subject only to its mass forces...
: the problem consist in finding the elastic equilibrium configuration
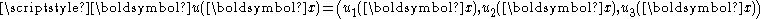 of an anisotropic non-homogeneous elastic body
of an anisotropic non-homogeneous elastic bodyPhysical body
In physics, a physical body or physical object is a collection of masses, taken to be one...
that lies in a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
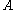 of the three-dimension
of the three-dimensionDimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
whose boundary
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
is
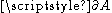 , resting on a rigid
, resting on a rigidRigid body
In physics, a rigid body is an idealization of a solid body of finite size in which deformation is neglected. In other words, the distance between any two given points of a rigid body remains constant in time regardless of external forces exerted on it...
frictionless surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
and subject only to its mass force
Weight
In science and engineering, the weight of an object is the force on the object due to gravity. Its magnitude , often denoted by an italic letter W, is the product of the mass m of the object and the magnitude of the local gravitational acceleration g; thus:...
s. The solution
 of the problem exists and is unique (under precise assumptions) in the set of admissible displacements
of the problem exists and is unique (under precise assumptions) in the set of admissible displacements 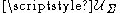 i.e. the set of displacement vectors satisfying the system of ambiguous boundary conditions if and only if
i.e. the set of displacement vectors satisfying the system of ambiguous boundary conditions if and only if
where
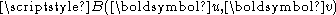 and
and 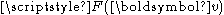 are the following functionals
are the following functionalsFunctional (mathematics)
In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...
, written using the Einstein notation
Einstein notation
In mathematics, especially in applications of linear algebra to physics, the Einstein notation or Einstein summation convention is a notational convention useful when dealing with coordinate formulae...
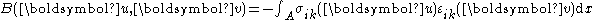
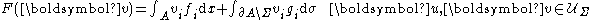
where, for all
 ,
,
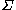 is the contact surfaceSurfaceIn mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
is the contact surfaceSurfaceIn mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
(or more generally a contact set),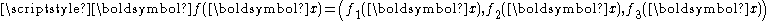 is the body forceBody forceA body force is a force that acts throughout the volume of a body, in contrast to contact forces.Gravity and electromagnetic forces are examples of body forces. Centrifugal and Coriolis forces can also be viewed as body forces.This can be put into contrast to the classical definition of surface...
is the body forceBody forceA body force is a force that acts throughout the volume of a body, in contrast to contact forces.Gravity and electromagnetic forces are examples of body forces. Centrifugal and Coriolis forces can also be viewed as body forces.This can be put into contrast to the classical definition of surface...
applied to the body,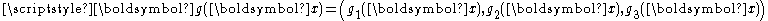 is the surface forceSurface forceSurface force denoted fs is the force that acts across an internal or external surface element in a material body. Surface force can be decomposed in to two perpendicular components: pressure and stress forces....
is the surface forceSurface forceSurface force denoted fs is the force that acts across an internal or external surface element in a material body. Surface force can be decomposed in to two perpendicular components: pressure and stress forces....
applied to ,
,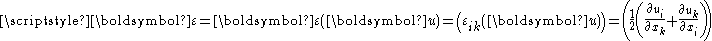 is the infinitesimal strain tensor,
is the infinitesimal strain tensor,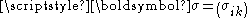 is the Cauchy stress tensor, defined as
is the Cauchy stress tensor, defined as
- where
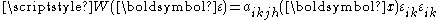 is the elastic potential energy and
is the elastic potential energy and 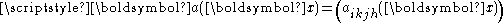 is the elasticity tensor.
is the elasticity tensor.
See also
- Complementarity theoryComplementarity theoryA complementarity problem is a type of mathematical optimization problem. It is the problem of optimizing a function of two vector variables subject to certain requirements which include: that the inner product of the two variables must equal zero, i.e. = 0...
- Differential variational inequalityDifferential variational inequalityIn mathematics, a differential variational inequality is a dynamical system that incorporates ordinary differential equations and variational inequalities or complementarity problems. DVIs are useful for representing models involving both dynamics and inequality constraints...
- Mathematical programming with equilibrium constraintsMathematical programming with equilibrium constraintsMathematical programming with equilibrium constraints is the study ofconstrained optimization problems where the constraints include variational inequalities or complementarities...
- Obstacle problemObstacle problemThe obstacle problem is a classic motivating example in the mathematical study of variational inequalities and free boundary problems. The problem is to find the equilibrium position of an elastic membrane whose boundary is held fixed, and which is constrained to lie above a given obstacle...
- Projected dynamical systemProjected dynamical systemProjected dynamical systems is a mathematical theory investigating the behaviour of dynamical systems where solutions are restricted to a constraint set. The discipline shares connections to and applications with both the static world of optimization and equilibrium problems and the dynamical world...
- Signorini problemSignorini problemThe Signorini problem is an elastostatics problem in linear elasticity: it consists in finding the elastic equilibrium configuration of an anisotropic non-homogeneous elastic body, resting on a rigid frictionless surface and subject only to its mass forces...